找工作中,可能要笔试,,有相关智力题,所以做了几道,今天发现了一个过桥问题,好像是一个比较经典的问题,微软用它做过笔试题。
过桥问题
问题:S个人晚上过桥,他们都站在桥的一端,桥上最多只能让N个人过桥。他们有一个手电筒,无论是一个人走还是k(k<=N)个人走,都需要手电筒。但人过桥后,手电筒不能扔过去,只能派人传过去。假设第i个人过桥的时间是Ti,则过桥的最短时间T(S)为?
解:不妨假设过桥时间T i
N递归方案:如果S<=N,则T(S)=max(T 1
另外还有一种N-1递归方案:如果S<=N,则T(S)=max(T 1
因为N递归方案不一定比N-1递归方案好,但N-1递归方案一定比N-2,…,1递归方案好(显而易见,能够照越多人过越好)
因此:
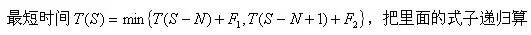
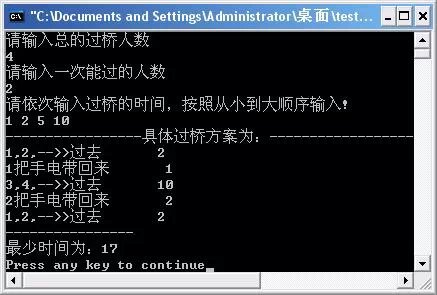
例1:S=4,N=2,四个人过桥时间依次为:1,2,5,10分钟。(微软面试题)
第一轮:F1=2+1+10+2=15,F2=10+1=11,T(4)=min{T(2)+15,T(3)+11}
第二轮:对于T(2)=2;对于T(3),F1=2+1+5+2=10,F2=1+5=6,所以T(3)=min{T(1)+10,T(2)+6}=min{11,8}=8。
代入第一轮,得出T(4)=min{2+15,8+11}=17
由于递归计算手算麻烦,编个简单c++程序如下(程序不排序,所以得严格输入):
#include<iostream.h>
int GetT(int *T,int n,int N,bool show)
{
if(n<=N)
{
if(show)
{
for(int i=0;i<n;i++)
cout<<i+1<<",";
cout<<"-->>过去"<<" "<<T[n-1]<<endl;
}
return T[n-1];
}
else
{
int F1=T[0]+T[1]+T[n-1]+T[N-1];
int F2=T[n-1]+T[0];
int T1=GetT(T,n-N,N,false)+F1;
int T2=GetT(T,n-N+1,N,false)+F2;
if(T1<T2)
{
if(show)
{
for(int i=0;i<N;i++)
cout<<i+1<<",";
cout<<"-->>过去"<<" "<<T[N-1]<<endl;
cout<<1<<"把手电带回来"<<" "<<T[0]<<endl;
for(i=0;i<N;i++)
cout<<n-N+1+i<<",";
cout<<"-->>过去"<<" "<<T[n-1]<<endl;
cout<<2<<"把手电带回来"<<" "<<T[1]<<endl;
GetT(T,n-N,N,true);
}
return T1;
}
else
{
if(show)
{
for(int i=1;i<N;i++)
cout<<n-N+i+1<<",";
cout<<1;
cout<<"-->>过去"<<" "<<T[n-1]<<endl;
cout<<1<<"把手电带回来"<<" "<<T[0]<<endl;
GetT(T,n-N+1,N,true);
}
return T2;
}
}
}
void main()
{
int S;
int N;
int ret;
cout<<"请输入总的过桥人数"<<endl;
cin>>S;
cout<<"请输入一次能过的人数"<<endl;
cin>>N;
int *T=new int[S];
cout<<"请依次输入过桥的时间,按照从小到大顺序输入!"<<endl;
for(int i=0;i<S;i++)
cin>>T[i];
cout<<"-----------------具体过桥方案为:------------------"<<endl;
ret=GetT(T,S,N,true);
cout<<"----------------"<<endl;
cout<<"最少时间为:"<<ret<<endl;
delete []T;
}
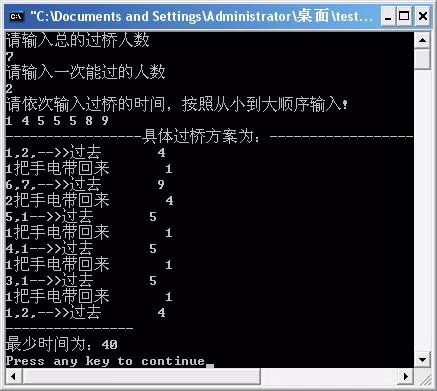
程序运行结果:
解:不妨假设过桥时间T i
N递归方案:如果S<=N,则T(S)=max(T 1
另外还有一种N-1递归方案:如果S<=N,则T(S)=max(T 1
因为N递归方案不一定比N-1递归方案好,但N-1递归方案一定比N-2,…,1递归方案好(显而易见,能够照越多人过越好)
因此:
例1:S=4,N=2,四个人过桥时间依次为:1,2,5,10分钟。(微软面试题)
第一轮:F1=2+1+10+2=15,F2=10+1=11,T(4)=min{T(2)+15,T(3)+11}
第二轮:对于T(2)=2;对于T(3),F1=2+1+5+2=10,F2=1+5=6,所以T(3)=min{T(1)+10,T(2)+6}=min{11,8}=8。
代入第一轮,得出T(4)=min{2+15,8+11}=17
由于递归计算手算麻烦,编个简单c++程序如下(程序不排序,所以得严格输入):
#include<iostream.h>
int GetT(int *T,int n,int N,bool show)
{
if(n<=N)
{
if(show)
{
for(int i=0;i<n;i++)
cout<<i+1<<",";
cout<<"-->>过去"<<" "<<T[n-1]<<endl;
}
return T[n-1];
}
else
{
int F1=T[0]+T[1]+T[n-1]+T[N-1];
int F2=T[n-1]+T[0];
int T1=GetT(T,n-N,N,false)+F1;
int T2=GetT(T,n-N+1,N,false)+F2;
if(T1<T2)
{
if(show)
{
for(int i=0;i<N;i++)
cout<<i+1<<",";
cout<<"-->>过去"<<" "<<T[N-1]<<endl;
cout<<1<<"把手电带回来"<<" "<<T[0]<<endl;
for(i=0;i<N;i++)
cout<<n-N+1+i<<",";
cout<<"-->>过去"<<" "<<T[n-1]<<endl;
cout<<2<<"把手电带回来"<<" "<<T[1]<<endl;
GetT(T,n-N,N,true);
}
return T1;
}
else
{
if(show)
{
for(int i=1;i<N;i++)
cout<<n-N+i+1<<",";
cout<<1;
cout<<"-->>过去"<<" "<<T[n-1]<<endl;
cout<<1<<"把手电带回来"<<" "<<T[0]<<endl;
GetT(T,n-N+1,N,true);
}
return T2;
}
}
}
void main()
{
int S;
int N;
int ret;
cout<<"请输入总的过桥人数"<<endl;
cin>>S;
cout<<"请输入一次能过的人数"<<endl;
cin>>N;
int *T=new int[S];
cout<<"请依次输入过桥的时间,按照从小到大顺序输入!"<<endl;
for(int i=0;i<S;i++)
cin>>T[i];
cout<<"-----------------具体过桥方案为:------------------"<<endl;
ret=GetT(T,S,N,true);
cout<<"----------------"<<endl;
cout<<"最少时间为:"<<ret<<endl;
delete []T;
}
程序运行结果:







 本文解析了一个经典的过桥问题,探讨了不同人数过桥时如何在有限条件下以最短时间完成。通过递归算法实现了问题求解,并给出了具体的实现代码。
本文解析了一个经典的过桥问题,探讨了不同人数过桥时如何在有限条件下以最短时间完成。通过递归算法实现了问题求解,并给出了具体的实现代码。
















 1万+
1万+










