PCA原理

PCA

各位，久违了～

什么是PCA？

什么是PCA呢？这是一个问题，什么样的问题？简单而又复杂的问题，简单是因为百度一下就会出现一大堆的解释，复杂是因为它里面蕴含的内容还是很多的，值得我们仔细研究研究。

PCA 取自其英文的三个单词的首字母：Principle component analysis。中文名字：主成分分析。恐怕大家很早就知道PCA是个什么东东，并且还用过matlab、python、C++等语言的各类机器学习算法包中的PCA函数进行数据处理。即便是没有自己写过这个PCA的程序可能也看过好多博客告诉我们：首先预处理数据，然后计算矩阵X的协防差阵。然后计算协防差阵的特征值和特征向量，最后根据特征值和特征向量建立一个映射矩阵…吧喇叭啦，一大堆的东西。然后感觉用编程实现这个过程应该也不是很难吧，然后就觉得自己会了PCA了，哈哈。

坦白说，上面是我的经历，并不是别人的经历，所以很惭愧，这个经历并不是很好，说实话，经过上面的经历我其实还是不知道什么是主成分分析，PCA对我来讲只是一个名字而已。但是为什么今天要写这篇文章呢？这是有原因的，因为之前看视频的时候发现视频中老师在讲PCA，重要的是老师不单单讲计算过程，而且讲了其中的原理。遗憾的是当时没听懂，也可能是当时睡着了，管他呢。最近写东西的时候遇到了和这个PCA相关的AutoEncoder，和学长交流的时候学长非常耐心地回答了我各种疑问，然后我知道了有AutoEncoder这个东西的存在，因为在这之前，我一直在考虑PCA。我靠，又跑题了，回归问题：什么是PCA？ 如果想记住这个名字的话很容易：三个字母PCA，po ci a 。如果想知道具体的内容和原理，往下看，当然，书本上，视频里都有，只不过我不能保证比下面的内容有趣。

PCA 用来干什么？

PCA呀，用来做什么呢？这个很重要，PCA也有很多应用，可能我们之前听过用PCA做人脸识别，PCA做异常检测等等。但事实上PCA没有那么强大的功能，PCA能做的事其实很有限，那就是：降维。其他拓展应用都是在这基础上做了相应额工作。为什要降维呢？很明显，数据中有些内容没有价值，这些内容的存在会影响算法的性能，和准确性。

如上图，数据点大部分都分布在x2方向上，在x1方向上的取值近似相同，那么对于有些问题就可以直接将x1坐标的数值去掉，只取x2坐标的值即可。但是有些情况不能直接这样取，例如：

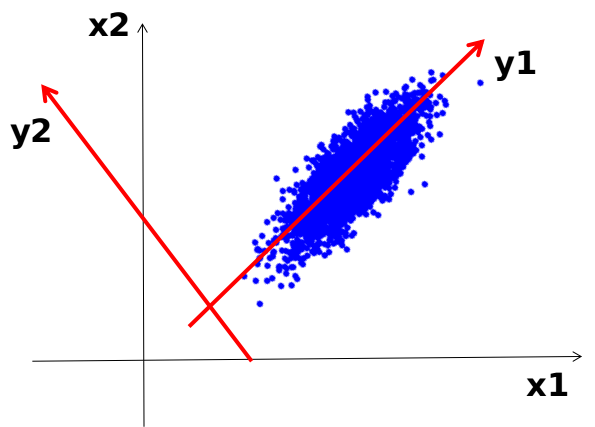
上图的数据分布在x1和x2方向都比较均匀，任一去掉一个坐标的数值可能对结果都会有很大的影响。这个时候就是PCA展现作用的时候了。黑色坐标系是原始坐标系，红色坐表系是我后面构建的坐标系，如果我的坐标系是红色的，那么这个问题是不是就和上面那个问题一样了，我只需要去掉y2坐标系的数据即可。实际上黑色坐标系和红色坐标系是等价的，差异仅仅是在空间中他们的基不同，黑色坐标系的基是我们最习惯的(1, 0), (0, 1)，红色坐标系的基是(1, 1),(-1, -1)，事实上，他们是等价的，只不过经常默认使用的就是黑色坐标系。主成分分析可以让数据的投影到那些数据分布比较分散的平面上，比如上图的y1，从而忽视y2的作用，进而达到降维的目的。

PCA 数学原理

为了达到目的，可以不择手段

上面我们说PCA可以将数据投影到分布分散的平面内，而忽略掉分布集中的平面。我们可以这样理解，如上面的图2,大部分数据投影到y1坐标系中的化，数据分布会比较分散，投影到x1、x2等其他坐标轴分布会相对集中，其中，投影到y2上面分布最集中。所以我们尽可能将数据转化到红色坐标系，然后去掉y2坐标。好了，问题描述完了，该想象怎样才能达到这样的目的。

任何形式的变化在数学上都可以抽象成一个映射，或者函数。好，现在我们需要构建一个函数$f(X_{m\times n})$使得这个函数可以将矩阵$X_{m\times n}$降维，矩阵$X$是原始数据，矩阵的每一行是一个样本的特征向量，即矩阵$X_{m\times n}$中有m个样本，每个样本有n个特征值。所以，所谓的降维，其实是减少n的数量。
假设降维后的结构为$Z_{m\times k}$，其中$k<n$
那么PCA的数学表达可以这样表示：
$$Z_{m\times k}=f(X_{m\times n}),k<n$$

这里可能比较抽象，我尽量说得有趣：

开始数学了，手段是数学

为了找到上面说的$f(x)$我们需要做一些工作，在线性空间中，矩阵可以表示为一种映射，所以上面的问题可以转化为寻找这样一个矩阵$W$，该矩阵可以实现上面的映射目的：
$$Z_{m\times k}=X_{m\times n}{W}_{n\times k}$$
都进行转秩吧，看着舒服，一般映射是放在左边的：

$$Z_{k\times m}=W_{k\times n}{X}_{n\times m}$$

现在假设我们要把矩阵的维数降为1,也就是最后每个样本只有一个属性,即$k=1$。
目标是使降维后的数据在那个坐标轴中的分布尽可能分散，数据的分布的离散程度我们用方差来衡量。
现在我们的目标：
$$z=wx$$

最大化新坐标轴上的方差，就是让数据更加分散：
$$\begin{gathered} \underset{w}{\max }\frac{1}{m}\sum _i^m(z_i-\bar{z}{)}^2 \\ s.t.\Vert W{\Vert }_2=1 \end{gathered}$$

将上面的优化问题转化一下：
$$\begin{gathered} \underset{w}{\max }\frac{1}{m}\sum _i^m(z_i-\bar{z}{)}^2 \\ =\underset{w}{\max }\frac{1}{m}\sum _i^m(w{x}_i-w\bar{x}{)}^2 \\ =\underset{w}{\max }\frac{1}{m}\sum _i^m(w(x_i-\bar{x}))(w(x_i-\bar{x}){)}^T \\ =\underset{w}{\max }\frac{1}{m}\sum _i^m(w(x_i-\bar{x})(x_i-\bar{x}{)}^T{w}^T{)}^T \\ =\underset{w}{\max }\frac{1}{m}w\sum _i^m(x_i-\bar{x})(x_i-\bar{x}{)}^T{w}^T \\ \underset{w}{\max }\frac{1}{m}wCov(x)w^T \end{gathered}$$

最终的目标转化为：
$$\begin{gathered} \underset{w}{\max }\frac{1}{m}wCov(x)w^T \\ s.t.\Vert w{\Vert }_2=1 \end{gathered}$$
$Cov(x)$是矩阵$x$的协防差阵。
利用lagrange multiplier 方法求解上面问题

$$\begin{gathered} L=\underset{w}{\max }\frac{1}{m}wCov(x)w^T+\alpha (\Vert w{\Vert }_2-1) \\ =\underset{w}{\max }\frac{1}{m}wCov(x)w^T+\alpha (w^{T}w-1) \end{gathered}$$
这里解释一下为什么要限制$\Vert w{\Vert }_2=1$，如果不这样限制，那么问题
$$\begin{gathered} \underset{w}{\max }\frac{1}{m}wCov(x)w^T \\ s.t.\Vert w{\Vert }_2=1 \end{gathered}$$
直接取$w=(\infty ,\infty ,...,\infty )$即可满足最大，那这样没有任何意义，所以这个限制条件是非常有用的。

通过求解 Lagrange 函数，得到结果为
$Cov(x)w-\alpha w=0$

令$Cov(x)=S$，$Sw-\alpha w=0$正好是特征值的定义，也就是$\alpha$是矩阵$S$的特征值，$w$是矩阵$S$的特征向量。但是特征值那么多，$w$到底是那个特征值呢？
$$\begin{gathered} \underset{w}{\max }\frac{1}{m}wS{w}^T \\ =\underset{w}{\max }{w}^T{S}^{T}w \\ =\underset{w}{\max }{w}^T\alpha w \\ =\alpha \underset{w}{\max }{w}^{T}w \\ =\alpha \end{gathered}$$

所以，要想最大化那个问题，就需要找到最大特征值。
同样道理，如果是需要将数据映射为2维数据，还是求解上述的最大化方差，但是需要加一个约束条件：$w_1\cdot w_2=0$，同样的思路，最终求解出$w_2$是第二大特征值对应的特征向量。更高维的计算以此类推。

经过上面一番推理，我们知道了PCA的原理，但是要记住PCA用途很广，但需要记住不是什么时候都可以用到PCA的，由证明过程我们知道PCA其实是有很多限制的。比如，可以做PCA降维的前提必须保证数据是线性分布的，如果数据不是线性的，比如下图这样的

数据分布不是线性的，用PCA效果可能就不会很理想。

PCA 用编程实现的流程

经过上面原理的推倒我们可以总结一下，真正进行PCA实际操作的时候都要经过哪些步骤？

1. 整理原始矩阵$X_{m\times n}$
2. 求原始矩阵$X_{m\times n}$的协防差阵$S_{m\times m}=Cov(X)$
3. 求解协防差阵的特征值和特征向量。
4. 选取最大的$K$(人为给定)个特征值所对应的特征向量组成构成矩阵$W_{n\times k}$
5. 直接进行矩阵计算$$Z_{m\times k}=X_{m\times n}{W}_{n\times k}$$

流程很明确，那具体的编程要怎么做呢？难点在哪？

难点1：协防差矩阵的计算

假设原始矩阵为$X_{m\times n}$，原始矩阵的各个属性的均值向量为$\bar{X}$
协防差距阵的计算如下：
$Cov(X)=\frac{1}{m}(X-\bar{X}{)}^T(X-\bar{X})$
这样用程序就非常好实现了。

难点2：特征值和特征向量的求解

特征值和特征向量这里的内容比较多，虽然有很多算法可以计算特征值和特征向量，但是其背后的数学原理着实有点复杂，记得有本书叫矩阵论，特征值和特征向量的计算方法和原理都可以在上面找到，惭愧的是，我也搞不懂。听说有什么QR算法、Jocobi方法、SVD等，似乎是一些矩阵分解的理论。这个还需要再好好学学才能继续吹牛，所以现在不能随便吹。

PCA等价于只包含一个隐层的神经网络

李宏毅老师的视频里用另外一种视角解释PCA，但是我觉得还是没有听明白，具体的关系，我觉得是老师没讲明白，其中最难以理解的就是$x-\bar{x}$和$\hat{x}$计算重构误差，为什么？？

所以这个理论还有待挖掘。

PCA和AutoEncoder的关系

1. PCA限制多，要求数据是线性分布的，AutoEncoder可以解决非线性降维问题
   《Reducing the Dimensionality of Data with Neural Networks》这篇论文中有详细介绍：
   下面是论文中实验的结果：
   
   

同样的数据，第一个图是PCA降维到2-D平面上的结果，第二个图是AutoEncoder降维到2-D平面上的结果。从结果中也可以明显的看出AutoEncoder降维后对数据的分布仍然有明显的区分，而PCA的结果却有点令人失望，好象是揉成了一团。

2. PCA理论基础更强，AutoEncoder可解释性差
   AutoEncoder通过挖掘潜在特性提高模型性能，但这些模糊的特性或许会对知识发现的结果产生不良影响。

3. PCA计算速度更快，AutoEncoder好不好，需要做实验验证

参考资料：

1. 李宏毅机器学习：PCA
2. Reducing the Dimensionality of Data with Neural Networks

掌管天堂的空之王者，于地狱唱响容光之歌！