2022强网杯CTF---强网先锋 ASR wp

原创已于 2023-10-17 17:09:17 修改 · 2.1k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #java #c++

于 2022-07-31 23:58:56 首次发布

CTF 专栏收录该内容

83 篇文章

订阅专栏

本文介绍了RSA加密的一个特殊实例，其中e和phi(n)的最大公约数为e本身，需要通过在有限域GF(p), GF(q), GF(r), GF(t)上分别对c开3次方根，再用中国剩余定理(CRT)组合解出m。解题脚本使用Sage数学软件完成，最终成功还原出加密的flag。

文章目录

题目

题目代码：

from Crypto.Util.number import getPrime
from secret import falg
pad = lambda s:s + bytes([(len(s)-1)%16+1]*((len(s)-1)%16+1))

n = getPrime(128)**2 * getPrime(128)**2 * getPrime(128)**2 * getPrime(128)**2
e = 3

flag = pad(flag)
print(flag)
assert(len(flag) >= 48)
m = int.from_bytes(flag,'big')
c = pow(m,e,n)

print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')

'''
n = 8250871280281573979365095715711359115372504458973444367083195431861307534563246537364248104106494598081988216584432003199198805753721448450911308558041115465900179230798939615583517756265557814710419157462721793864532239042758808298575522666358352726060578194045804198551989679722201244547561044646931280001
e = 3
c = 945272793717722090962030960824180726576357481511799904903841312265308706852971155205003971821843069272938250385935597609059700446530436381124650731751982419593070224310399320617914955227288662661442416421725698368791013785074809691867988444306279231013360024747585261790352627234450209996422862329513284149
'''

思路

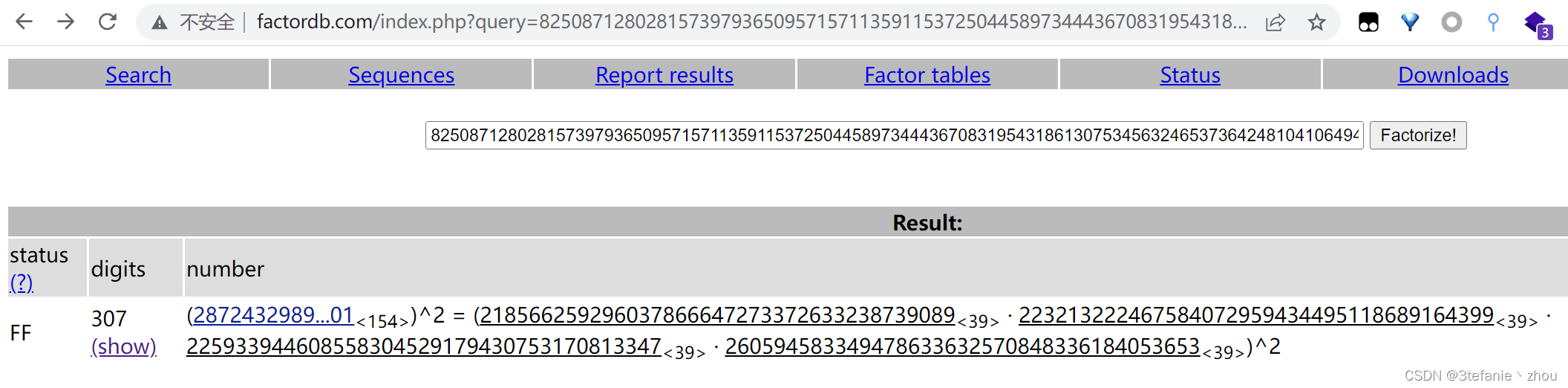
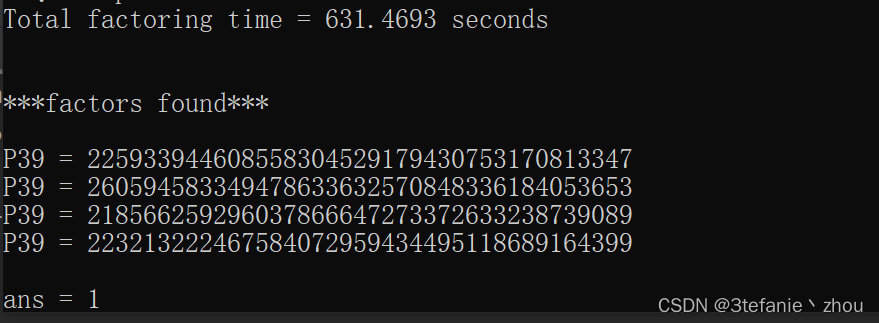
首先对n进行分解得到4个素数，p、q、r、t，可以使用在线的factordb网站分解，也可以用yafu（使用该工具建议先开方，然后将其值再分解）

在线分解网站
factordb分解结果
在这里插入图片描述
yafu分解结果

分解得到四个素数如下

p = 225933944608558304529179430753170813347
q = 260594583349478633632570848336184053653
r = 218566259296037866647273372633238739089
t = 223213222467584072959434495118689164399

正常情况下的RSA都要求e和phi(n)要互素，不过也有一些e和phi(n)有很小的公约数的题目，这些题目可以通过计算e对phi(n)的逆元d来求解。但是本题则为e和phi(n)的最大公约数就是e本身，也就是说e | p-1，只有对c开e次方根才行,到这里就是一个有限域开3次方根的问题了。
PS:上述中的phi(n)也可以是，（p-1）或者（q-1）或者（r-1）或者（t-1）

将同余方程
$m^e \equiv c \quad (\text{mod}\ n)$
简化为
$m^e \equiv c \quad (\text{mod}\ p)$
$m^e \equiv c \quad (\text{mod}\ q)$
$m^e \equiv c \quad (\text{mod}\ r)$
$m^e \equiv c \quad (\text{mod}\ t)$
然后分别在GF（p）、GF(q)、GF（r）、GF(t)上对c开e=3次方根，再用CRT组合一下即可得到在mod n下的解

解题脚本

sage脚本如下

import libnum
n = 8250871280281573979365095715711359115372504458973444367083195431861307534563246537364248104106494598081988216584432003199198805753721448450911308558041115465900179230798939615583517756265557814710419157462721793864532239042758808298575522666358352726060578194045804198551989679722201244547561044646931280001
e = 3
c = 945272793717722090962030960824180726576357481511799904903841312265308706852971155205003971821843069272938250385935597609059700446530436381124650731751982419593070224310399320617914955227288662661442416421725698368791013785074809691867988444306279231013360024747585261790352627234450209996422862329513284149
p = 225933944608558304529179430753170813347
q = 260594583349478633632570848336184053653
r = 218566259296037866647273372633238739089
t = 223213222467584072959434495118689164399

R.<x> = Zmod(p)[]
f = x^e-c
f = f.monic()
results1 = f.roots()

R.<x> = Zmod(q)[]
f = x^e-c
f = f.monic()
results2 = f.roots()

R.<x> = Zmod(r)[]
f = x^e-c
f = f.monic()
results3 = f.roots()

R.<x> = Zmod(t)[]
f = x^e-c
f = f.monic()
results4 = f.roots()
for i in results1:
    for j in results2:
        for l in results3:
            for k in results4:
                param1 = [int(i[0]),int(j[0]),int(l[0]),int(k[0])]
                param2 = [p,q,r,t]
                m = CRT_list(param1,param2)
                flag = libnum.n2s(int(m))
                if b'flag' or b'gwb' or b'FLAG' or b'GWB' in flag:
                    print(flag)

flag:

flag{Fear_can_hold_you_prisoner_Hope_can_set_you_free}

【有些不愿开口与人说的委屈，来自得不到身边人的回应，种种期许、憧憬、愿望之心声，在心中如擂鼓，响彻自己天地间。心外却哑然，永远寂静无声，这就像一个人把嗓子喊哑了，身边还是无人听见，这个人就会越来越不喜欢说话，一直沉默下去，直到变成一个哑巴。】