数据结构—队列的实现（顺序表）

数据结构中的队列有“先进先出”的特点，意思是最先被存进队列中的数据，总是最先被取走

一个队列只有初始化，销毁，入队列，出队列和取队首元素，这些限制往往使在操作数据时更安全，代码容易实现，出现BUG的机会就很少

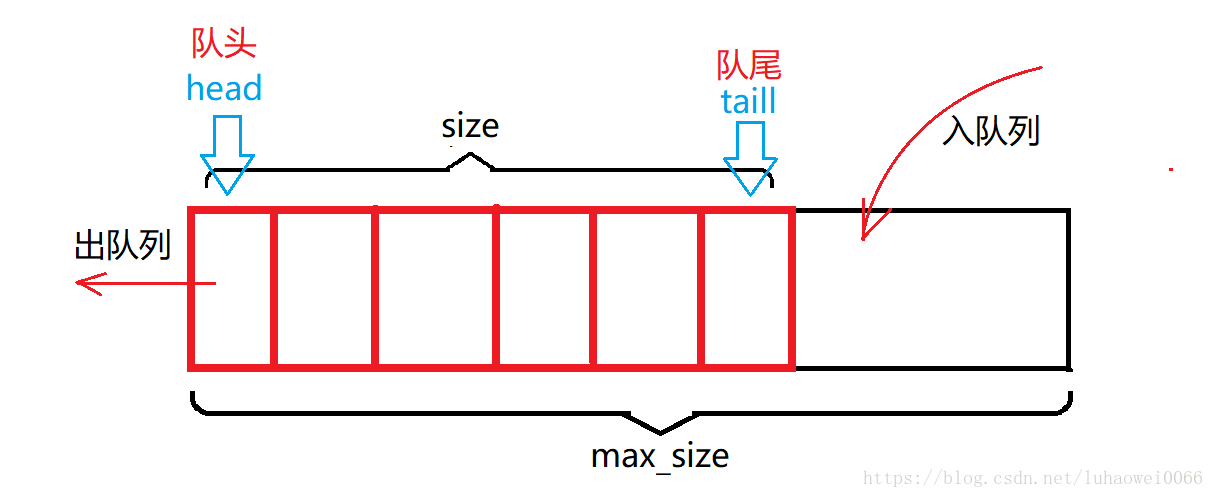
上图队列，如过进行了多次入队列和出队列，就会是head之前的空间浪费，如下图

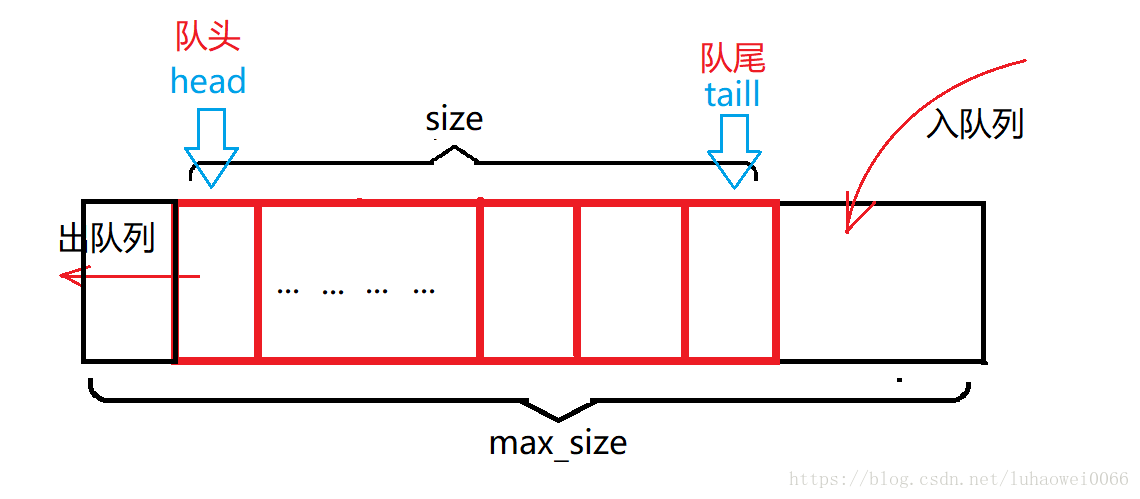
为了避免这种浪费空间的测操作，当每次head 和 tail 只要到达最后一个元素，操作完成就让他们回到对列的最前面，即head = 0 或 tail = 0，这样head == taill 时，可能是空对列，也可能是满对列，所以判断对列是否满了出现困难，在对列的机构体中加上一个size成员，用来判断是否对列已满

头文件（SeqQueue.h）

#pragma once

typedef char QueueType;

typedef struct SeqQueue{
    QueueType* place;   //队列的空间
    size_t head;        //队首标记
    size_t tail;        //队尾标记
    size_t size;       //对列当前存储元素的个数
    size_t max_size;  //对列最大存储元素个数
}SeqQueue;


void SeqQueueInit(SeqQueue* queue);  //队列初始化

void DestroyQueue(SeqQueue* queue);    //销毁队列

void SeqQueueIn(SeqQueue* queue, QueueType value);    //入队列

void SeqQueueOut(SeqQueue* queue);    //出队列

int SeqQueueFront(SeqQueue* queue, QueueType* output_value);     //取队首元素

头文件的实现（SeqQueue.c）

#include<stdio.h>
#include<stdlib.h>
#include"SeqQueue.h"

void SeqQueueInit(SeqQueue* queue) {
    queue->max_size = 1;
    queue->size = 0;
    queue->head = 0;
    queue->tail = 0;
    queue->place = malloc(queue->max_size * sizeof(SeqQueue));
    if(queue->place == NULL) {
        printf("malloc 失败！\n");
        exit(1);
    }
}

void DestroyQueue(SeqQueue* queue) {
    if(queue == NULL) {
        return;
    }
    free(queue->place);
    queue->place = NULL;
    queue->max_size = 0;
    queue->size = 0;
    queue->head = 0;
    queue->tail = 0;
}

void SeqQueueIn(SeqQueue* queue, QueueType value) {
    if(queue == NULL) {
        return;
    }
    if(queue->size >= queue->max_size) {
        queue->max_size = 2 * queue->max_size + 1;
        QueueType* new_place  = malloc(queue->max_size * sizeof(SeqQueue));
        int i = 0;
        if(queue->tail == queue->head) {
            for(i = 0; i < queue->tail; i++) {
                new_place[i] = queue->place[i];
            }
            queue->tail = i;
            for(i = 1; i <= (queue->size - queue->head); i++) {
                new_place[queue->max_size - i] = queue->place[queue->size - i];
            }
            queue->head = queue->max_size - i;
        }
        else if(queue->tail > queue->head) {
            for(i = 0; i < queue->size; i++) {
                new_place[i] = queue->place[i];
            } 
        }
        free(queue->place);
        queue->place = new_place;
    }
    if(queue->tail == queue->max_size) {
        queue->tail = 0;
    }

if(queue->head == queue->max_size) {
        queue->head = 0;
    }

queue->place[queue->tail] = value; queue->tail++; queue->size++;}void SeqQueueOut(SeqQueue* queue) { if(queue == NULL) { return; } if(queue->size == 0) { return; } if(queue->head == queue->max_size) { queue->head = 0; } queue->head++; queue->size--;}int SeqQueueFront(SeqQueue* queue, QueueType* output_value) { if(queue == NULL || output_value == NULL) { *output_value = 0; return 0; } if(queue->size == 0) { *output_value = 0; return 0; }    
*output_value = queue->place[queue->head]; return 1;}/////////////////////////////////////////////////////以下为测试代码///////////////////////////////////////////////////void TestQueue() { SeqQueue queue; SeqQueueInit(&queue); SeqQueueIn(&queue, 'a'); SeqQueueIn(&queue, 'b'); SeqQueueIn(&queue, 'c'); SeqQueueIn(&queue, 'd'); int ret; QueueType value; ret = SeqQueueFront(&queue, &value); printf("expected a, actrual %c\n", value); printf("expected 1, actrual %d\n", ret); SeqQueueOut(&queue); ret = SeqQueueFront(&queue, &value); printf("expected b, actrual %c\n", value); printf("expected 1, actrual %d\n", ret); SeqQueueOut(&queue); ret = SeqQueueFront(&queue, &value); printf("expected c, actrual %c\n", value); printf("expected 1, actrual %d\n", ret); SeqQueueOut(&queue); ret = SeqQueueFront(&queue, &value); printf("expected d, actrual %c\n", value); printf("expected 1, actrual %d\n", ret); SeqQueueOut(&queue); ret = SeqQueueFront(&queue, &value); printf("expected 0, actrual %d\n", value); printf("expected 0, actrual %d\n", ret); SeqQueueOut(&queue);}int main(){ TestQueue(); return 0;}

实验结果

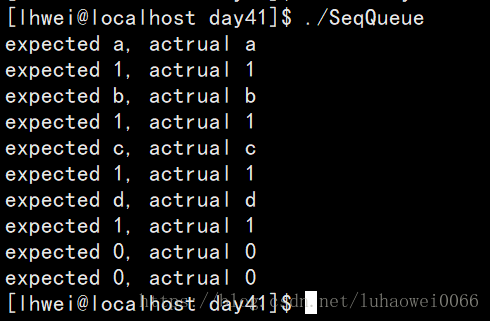
补充：队列满了的情况有两种

第一种：

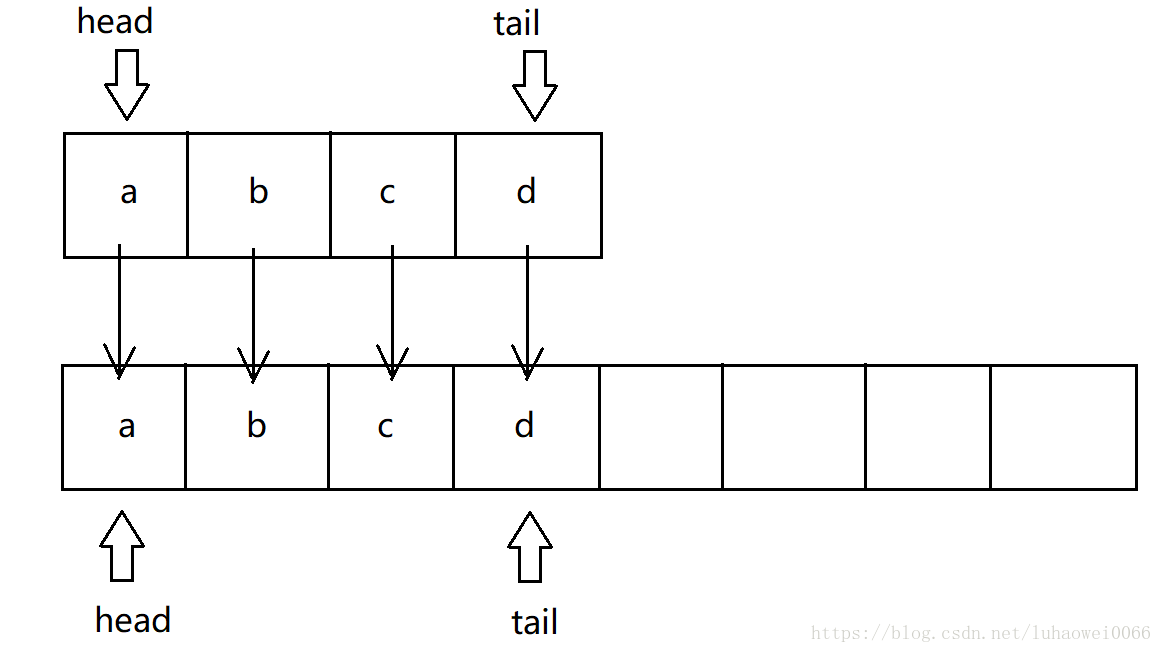
只需要从旧的空间把head和tail之间的数据对应复制到新的空间

第二种：

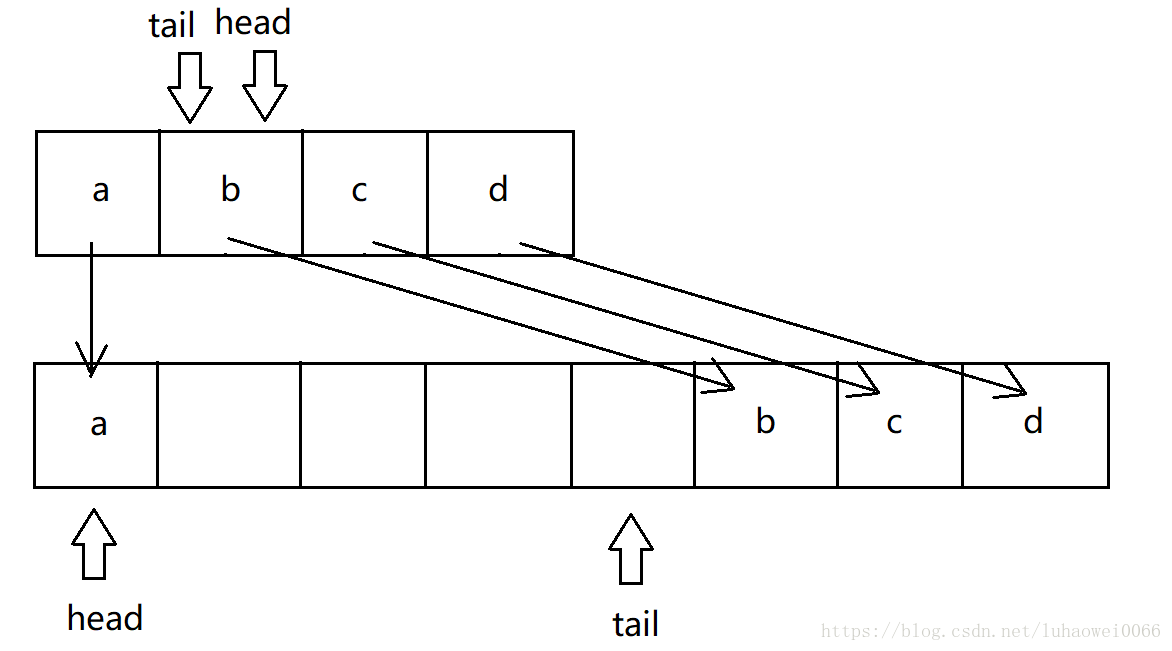
把旧0-tail的数据复制到新空间的0-tail

把head到最后一个数据 之间的数据按顺序复制到新空间的最后面