计算机十六进制

进制概念

进制也就是进位制。进行加法运算时逢X进一（满X进一），进行减法运算时借一当X，这就是X进制，这种进制也就包含X个数字，基数为X。

十六制运算

进位规则：“逢16进1”
借位规则：“借1当16”
基数：16
数码：0~F 【0~9、A、B、C、D、E、F 】
后缀：用H、16或0X来表示，例如：（1010）16、（1010）H、0X1010
位权：从最低位（最右边）开始，依次表示16的0次方，16的1次方，以此类推

1) 十六进制加法：6+7=D、18+BA=D2、595+792=D27、2F87+F8A=3F11

2) 十六进制减法：D-3=A、52-2F=23、E07-141=CC6、7CA0-1CB1=5FEF

十六进制转换

转换二进制 ：

十六进制整数转换为二进制整数时，每一位十六进制数字转换为四位二进制数字，运算的顺序也是从低位向高位依次进行。下图演示了如何将十六进制整数 A5D6 转换为二进制：

1) 整数部分：
将十六进制整数 A5D6 转换为二进制：

2）小数部分：
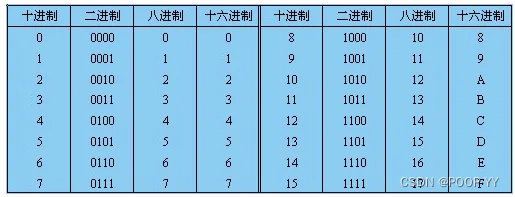
通过十六进制对应十进制，再查到十进制对应的二进制，然后就可以得出如下结论：
2： 0010
1： 0001
0： 0000
4： 0100
那么，21.04H=0010 0001.0000 0100
而实际上计算机输出结果一般会去掉头尾多余的0，所以实际输出结果可能为：1000001.000001

转换十进制

1）整数部分：

2AF5换算成10进制:
第0位：5*16^0 = 5
第1位：F*16^1 = 15*16^1 = 240
第2位：A*16^1 = 10*16^2 = 2560
第3位：2*16^3 = 8192
结果 = 5 + 240 + 2560 + 8192
可以看出，所有进制换算成10进制，关键在于各自的权值不同

2）小数部分：

1C2D.9=1*16^3+C*16^2+D*16^0+9*16^-1(16的负1次方)=7213.5625，16进制ABCDEF对应十进制为10，11，12，13，14，15。

转换八进制

1）整数部分：
十六进制数053977，将其转换成二进制001 010 011 100 101 110 111，再将该二进制转换为八进制，可得八进制数为1234567
3BC24

分别对应到上表（二进制） 是：
0011 1011 1100 0100
再按照每三个一组分组：
0 011 101 111 000 100
对应到8进制：
0__3__5__7__0__4
所以8进制就是35704

2）小数部分：

16进制转换8进制方法 —— 3BC24.3 转二进制，再转八进制。
3BC24.3 = 111011110000100100.0011(二进制)
        = 421 421 421 421 421 421 421 421   
        = 111 011 110 000 100 100.001 100
        = 7    3   6   0   4   4 . 1   4                        
转八进制000 011 100.110 100()就是034.64去0 就是34.64