只出现一次的数字，LeetCode可通过。

最新推荐文章于 2025-12-20 20:19:18 发布

原创最新推荐文章于 2025-12-20 20:19:18 发布 · 200 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#找出那个只出现了一次的元素 #leetcode #异或运算

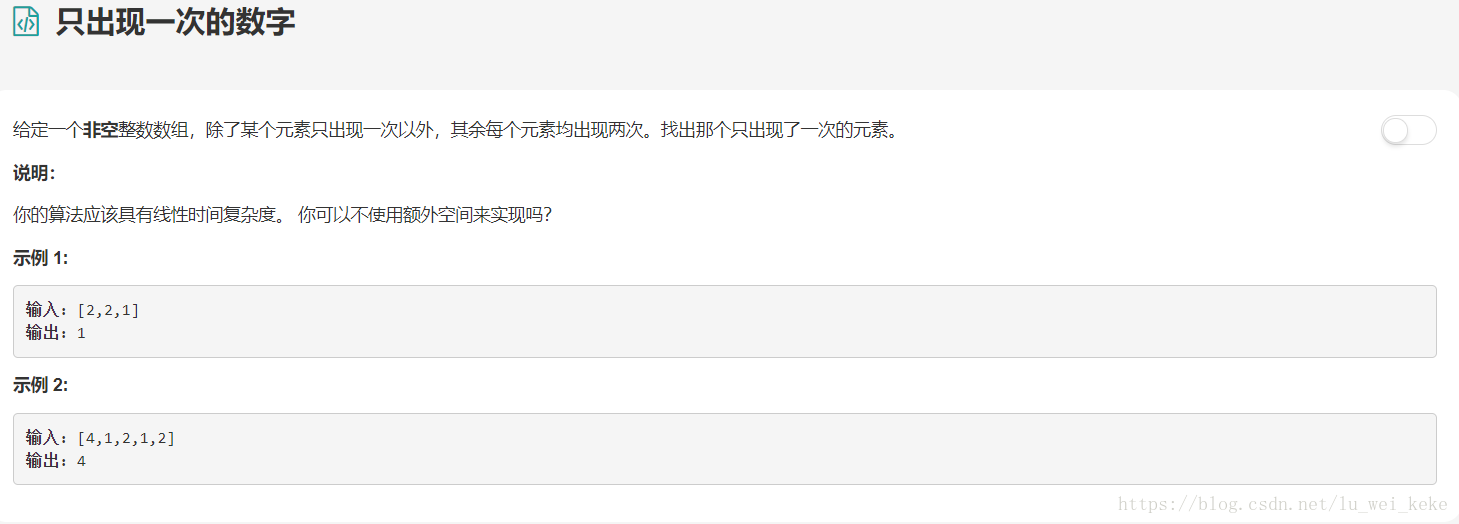
这个题目只是看题目的话是很简单的，但是说明中有一条是应该算法具有线性时间复杂度 ，这一点我是真的百思不得其解。只能先自己实现一下这个功能，但是我的时间复杂度为O(n²)

代码如下：

class Solution {
    public int singleNumber(int[] nums) {
        int temp=nums[0];
        boolean tmp=false;
         for(int i=0;i<nums.length-1;i=i+2){
             for(int j=i+1;j<nums.length;j++){
                 if(nums[i]==nums[j]){
                    temp= nums[i+1];
                    nums[i+1]=nums[j];
                     nums[j]=temp;
                     tmp=true;
                     break;
                 }
             }
             if(!tmp)return nums[i];
             tmp=false;
         }
         
        return nums[nums.length-1];
    }

}

我的算法是通过两个for循环，主要是在第二个循环中找到与nums[i]相等的数再将这个数与nums[i+1]交换。

虽然这样能够通过，但是还是不符合题目要求。

然后我就上网搜了一下发现有这篇文章:http://www.cnblogs.com/ralap7/p/9025040.html

表示献出我的膝盖。

我稍微讲一下思路：异或运算---->一个神奇的东西。

异或的特点：

① 任何数与0异或会得到它本身。即：n^0=n

② 任何数与它自身异或会得到0。即：n^n=0

③ 异或运算是支持交换律跟结合律。即：1^2^1^2=1^1^2^2=0^0=0

所以最后的结果如下：

class Solution {
    public int singleNumber(int[] nums) {
        int temp=0;
        for(int i=0;i<nums.length;i++){
            temp^=nums[i];
        }
        return temp;
    }

}

题目来源：https://leetcode-cn.com

思路修正来源：http://www.cnblogs.com/ralap7/p/9025040.html