基本排序算法

博客源于：一周刷爆LeetCode，算法大神左神（左程云）

时间复杂度

常熟操作：

和数据量有关的操作比如+、-、*、/为参数操作。

时间复杂度

拿简单的选着排序为例子

第一轮在整个序列里找到最小的值和第一个位置的数进行交换，然后在1到N-1的的区间找最小值和1位置的数进行交换。把每个步骤的常数操作都记录下来。
可以得到表达式

只取最高阶项所有为O(N^2).
如果最高阶项相同则看实际跑的情况那个算法比较好。
选着排序代码如下：

void swap(int *arry,int i,int j)
{
    int tmp=0;
    tmp=arry[i];
    arry[i]=arry[j];
    arry[j]=tmp;
}
//选择排序(一次选一个数)
void SelectSort(int* a, int n)
{
	int i = 0;
	for (i = 0; i < n; i++)//i代表参与该趟选择排序的第一个元素的下标
	{
		int start = i;
		int min = start;//记录最小元素的下标
		while (start < n)
		{
			if (a[start] < a[min]) min = start;//最小值的下标更新
			start++;
		}
		swap(a,i,min);//最小值与参与该趟选择排序的第一个元素交换位置
	}
}

额外空间复杂度

因为只是用了有限几个变量，i，satrt，min所有额外空间复杂度为（0）

简单排序

冒泡排序

上面的是数字序列，下面的是位置。0和1位置的的数字进行比较小的放左边，大的放右边。然后交换区间往后移继续比较交换。这样一轮下来最大的数就来到了5位置，这样5位置的数就搞定了

整个排序算法跑下来就是构成一个等差数列的前N项和所有还是O(N^2)的算法

代码演示：

void maopaosort(int*arry, int size)
{
	if (arry==NULL)
	{
		return;
	}
	int rang_size=size;
	for (int i = 0; i < size; i++)
	{
		for (int i = 0; i < rang_size-1; i++)
		{
			if (arry[i]>arry[i+1])
			{
				swap(arry,i,i+1);
			}
		}
	}
}

关于异或运算


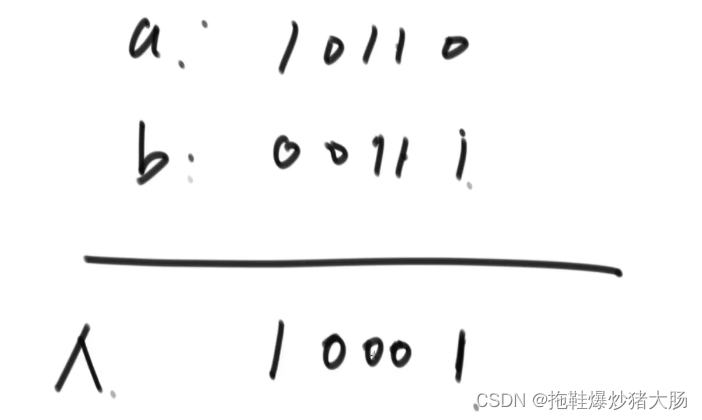
两个数交换：

int a=17;
int b=9;
a=a^b;
b=a^b;
a=a^b;

注意：这种操作的前提是变量a和变量b是两块独立的内存。不然同样的内存区域和自己异或对把自己洗成零。

插入排序

先左到0-0范围内有序，然后要做到0-1范围内有序，向前看，如果右边的值比左边的值小就做交换。

所有2这个数就来到了0这个位置，然后2再往前看，但是没有数了，就可以停了，这样就做到了0-1范围内有序了。

然后就从二个位置上的数开始看，显然，5比3大所有就做到了0-2范围内的数有序了，依次往后是数字往前看，小的就交换，如果不小了就停止这样就做到了前面的数已经有序了。

代码演示：

//插入排序
void InsertSort(int* a, int n)
{
	int i = 0;
	for (i = 0; i < n - 1; i++)
	{
		int end = i;//记录有序序列的最后一个元素的下标
		int tmp = a[end + 1];//待插入的元素
		while (end >= 0)
		{
			if (tmp < a[end])//还需继续比较
			{
				a[end + 1] = a[end];
				end--;
			}
			else//找到应插入的位置
			{
				break;
			}
		}
		a[end + 1] = tmp;
		//代码执行到此位置有两种情况:
		//1.待插入元素找到应插入位置（break跳出循环到此）。
		//2.待插入元素比当前有序序列中的所有元素都小（while循环结束后到此）。
	}
}

数据状况不同它的时间复杂度的不同，前面的排序算法不管数据状况什么样都不影响时间复杂度。（所有算法对时间复杂度的评估都是按照最差的情况来估估计的。）

有序数组中的二分查找

在有序数组中，因为数组有序所有直接比较中点看看是还是小，就可以判断查找到对象在左边还是右面，这样就可以缩小查找的数据区间。

求局部最小（使用二分）

既比左边的数小，又比右边的数小

无序的数据状况使用二分策略

master公式（要求子问题规模一样）

只要满足下面行为的递归它的时间复杂度可以直接求

调用子问题的时候规模是不是等量的，是不是N/b的规模，a表示子问题是等量的情况下被调了多少次，最后面的部分表示除去调用子过程之外剩下过程调用的时间复杂度。

例如在下面面在左侧三分之二部分求一次递归

master公式的时间复杂度

归并排序

通过递归过程让左侧部分和右侧部分排好序，然后准备一个辅助空间和两个指针（不是C语言的指针）指向两侧前面的数，然后两个数比较，谁小就拷贝谁到这个辅助空间上去，然后指针往后移动，当两个想等的时候默认拷贝先拷贝左边的。

如果与一侧越界了就可以把另外一侧剩下的部分全部拷贝到辅助空间。

代码演示：

int Cls_MergeSorter::MergeSort(int *arr,int size)
{
	if (size<2)
	{
		return 0;
	}
	MergeSort(arr,0,size);
	return 0;
}

int Cls_MergeSorter::MergeSort(int *arr,int r,int l)
{
	int mid=0;
	if (r==l)
	{
		return 0;
	}
	mid=r+((l-r)>>1);
	MergeSort(arr,r,mid);
	MergeSort(arr,mid+1,l);
	Merge(arr,r,mid,l);
	return 0;
}

int Cls_MergeSorter::Merge(int *arr,int r,int mid,int l)
{
	int *help=new int[l-r+1];
	int i=0;
	int p1=r;
	int p2=mid+1;
	while(p1<=mid&&p2<=l) //两个下标都没有越界
	{
		help[i++]=arr[p1]<arr[p2]?arr[p1++]:arr[p2++];
	}
	while(p1<=mid)  //如果p1没有越界就把p1剩下的拷贝到辅助空间里面去
	{
		help[i++]=arr[p1++];
	}
	while (p2<=l)//如果p2没有越界就把p2剩下的拷贝到辅助空间里
	{
		help[i++]=arr[p2++];
	}
	for ( i=0; i < l-r+1; i++)
	{
		arr[r+i]=help[i];
	}
	delete[] help;
	return 0;
}

归并排序的时间复杂度
满足master公式

为什么O(NlogN) 好在那里？冒泡排序和插入排序都是浪费了大量的比较行为才搞定了一个数。归并排序没有浪费比较行为，而是把比较行为变成部分有序。

荷兰国旗问题

问题：把小于num的数分到左边，大于num的数分到右边？
解决办法：设置一个小于等于区，num和小于等于区的一个数比较，如果比num小的话就把小于等于区域往右边阔大，然后指向下一个进行比较，如果比较的数比num大的话就跳跳下一个继续比较，如果跳到了的数比num小则该数与小于等于区的前一个数交换，交换后将小于等于去往外扩，当指向的数字指到的最后的时候就可完成将数据以num为边界的数据划分。

荷兰国旗问题：将小于num数放左边，等于num的数放中间，大于num的数放右边。

快速排序1.0

每次都是以最后一个数做划分，划分好了就将大与等于区的一个数与划分值num做交换，这样小于等于区就会被扩充了，然后继续在小于等于区域和大于区域继续做划分，递归进行分层做划分，每次递归都能是一个数被拍好。

代码演示：

void Cls_QuickSort::QuickSort(int *arry,int size)
{
	if (size<2)
	{
		return;
	}
	else
	{
		QuickSort(arry,0,size-1);	
	}
	
}

void Cls_QuickSort::QuickSort(int *arry,int l,int r)
{
	int*p=NULL;
	if (l<r)
	{
		p=NetherlandsFlag(arry,l,r,arry[r]);
		QuickSort(arry,l,p[0]);
		QuickSort(arry,p[1],r);
		delete[] p;
	}
}

int* Cls_QuickSort::NetherlandsFlag(int *arry,int l,int r,int p)
{
	int less=l-1;
	int more=r+1;
	int *point;
	point=new int[2];
	while (l<more)
	{
		if (arry[l]<p)	//小于下划分值
		{
			swap(arry,++less,l++);	//与小于区的前一个数做交换，小于区less往右扩，l跳下一个数
		}
		else if (arry[l]>p) //大于下划分值
		{
			swap(arry,--more,l);//与大于区的前一个数做交换，大于区less往左扩，l不变应为新换过来的数数到了l位置还没有进行比较。
		}
		else	//等于划分值则跳过
		{
			l++;
		}
	}
	point[0]=less;//返回小于区边界，以便下轮使用这一边界做划分
	point[1]=more;//返回大于区边界以便下轮使用这一边界做划分
	return point;
}

快速排序2.0

把最后一个数拿出来做划分，小于5的放左边，等于五的放中间，大于5的放左边，然后最后一个数5和大于区的第一个数做交换等于区往右阔，这样就可以搞定等于五的一批数，然后再对小于区和大于区这样做划分，递归进行这样每次递归就搞定了以匹数num的位置。快排2.0比快排1.0快一些，因为2.0每次搞定以批等于num划分值的是

快速排序最差情况下的时间复杂度，（划分值选的很偏的情况），会退化为O（N^2）的算法。好情况是选择做划分的数正好在中间，
如下：划分值为9，每次递归的划分值都很扁，就会退化为一个时间复杂度为O（N^2）的算法。

快速排序3.0

随机选一个数出来做划分，然后把它跟最右侧的数做交换，然后做递归分层。因外划分值好的情况和差的情况是等概率的所有求熟悉的长期期望后，得到是时间复杂度为O(N*logN)

堆

完全二叉树

大根堆

以6为父节点的最大值是6，以5为父节点的最大值是5一次类推，每一颗子树对最大点为头节点。

调整为大根堆步骤

每来一个数就和自己的父节点进行比较，如果大于父节点的话就和父节点进行交换，一直往上和自己的父节点交换直到不比自己的父节点大节停止向上调整。

代码演示：

//某个数现在处于index位置，往上移动，向上调整，调整为大根堆
int Cls_HeapSort::HeapInsert(int *arry,int index)
{
	while (arry[index]>arry[(index-1)/2]) //和自己的父节点比较
	{
		swap(arry,index,((index-1)/2)); //交换
		index=(index-1)/2;	//索引继续向上指向自己，以便往上继续比较
	} 
	return 0;
}

对的向下调整

用户需求：将最大值拿出并从堆中移除。
解决办法：将堆中最后一个数从堆中挪到树的根节点，然后堆大小减一。然后让两个子节点比较，那个孩子大就跟那个孩子交换。然后继续往下比较和交换。

堆中任意节点向下调整代码

//index为要进行向下调整的节点
int Cls_HeapSort::Heapify(int *arry,int index,int heapsize)
{
	int left=index*2+1;
	int largest=0;
	while (left<heapsize)	 //下方有孩子的时候
	{
		//是否有右孩子，与右孩子大于左孩子则把右孩子的下标给largest
		largest=left+1<heapsize&&arry[left+1]>arry[left]?left+1:left;  
		//父亲与较大孩子作比较，谁大，就把下标给largest
		largest=arry[largest]>arry[index]?largest:index;
		if (largest==index)
		{
			break;
		}
		swap(arry,largest,index);
		index=largest;//父节点往下走
		left=index*2+1;
	}
}

堆排序

堆排序步骤：先是HeapInsert构建一个大根堆，然后将根节点（树中的最大值）与堆中的最后一个数做交换，然后对对大小减一，这样就完成了一个数的排序。然后继续使用Heapify向下调整，调整成大根堆，然后继续将最大值取出来与堆的尾部做交换，堆大小减一。当堆大小被减为0的时候，堆排序完成。

代码演示：

int Cls_HeapSort::HeapSort(int *arry,int size)
{
	if (NULL==arry||size<2)
	{
		return-1;
	}
	for (int i = 0; i < size; i++)
	{
		HeapInsert(arry,i);
	}   
	swap(arry,0,--size);
	while (size>0)
	{
		Heapify(arry,0,size);
		swap(arry,0,--size);
	}
}

//某个数现在处于index位置，往上移动，向上调整，调整为大根堆
int Cls_HeapSort::HeapInsert(int *arry,int index)
{
	while (arry[index]>arry[(index-1)/2]) //和自己的父节点比较
	{
		swap(arry,index,((index-1)/2)); //交换
		index=(index-1)/2;	//索引继续向上指向自己，以便往上继续比较
	} 
	return 0;
}

//index为要进行向下调整的节点
int Cls_HeapSort::Heapify(int *arry,int index,int heapsize)
{
	int left=index*2+1;
	int largest=0;
	while (left<heapsize)	 //下方有孩子的时候
	{
		//是否有右孩子，与右孩子大于左孩子则把右孩子的下标给largest
		largest=left+1<heapsize&&arry[left+1]>arry[left]?left+1:left;  
		//父亲与较大孩子作比较，谁大，就把下标给largest
		largest=arry[largest]>arry[index]?largest:index;
		if (largest==index)
		{
			break;
		}
		swap(arry,largest,index);
		index=largest;//父节点往下走
		left=index*2+1;
	}
}

堆排序的时间复杂度为：O（N*logN）
而外空间复杂度：O(1)