CS231n——机器学习基础算法

KNN（K-近邻算法）

原理

有监督学习。
已有一堆正确分类的数据集，对于新的数据，通过计算在新数据的一定距离内的数据中，哪类数据占优(投票)，判定新的数据的类别。

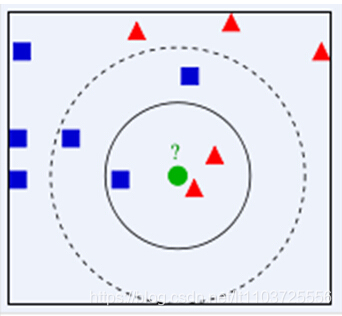
k——离新数据最近的数据个数(总投票数)
距离

L1距离或L2距离，见CS231n学习笔记

L1距离：$d_1\left(I_1,I_2\right)={\sum }_p\left|I_1^p-I_2^p\right|$
又称曼哈顿距离，即每个对应位置相减再求和
L2距离：$d_2\left(I_1,I_2\right)=\sqrt{{\sum }_p{\left(I_1^p-I_2^p\right)}^2}$
又称欧式距离，每个对应位置相减平方和开根
区别：L1距离依赖于数据的坐标系统，也就是说数据的向量的每个值都有不同的意义时用L1更合适

L2距离的矩阵描述

矩阵的欧式距离
参考https://blog.youkuaiyun.com/frankzd/article/details/80251042

算法描述

1）计算测试数据与各个训练数据之间的距离；
2）按照距离的递增关系进行排序；
3）选取距离最小的K个点；
4）确定前K个点所在类别的出现频率；
5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

SVM（支撑向量机）

Bias Trick

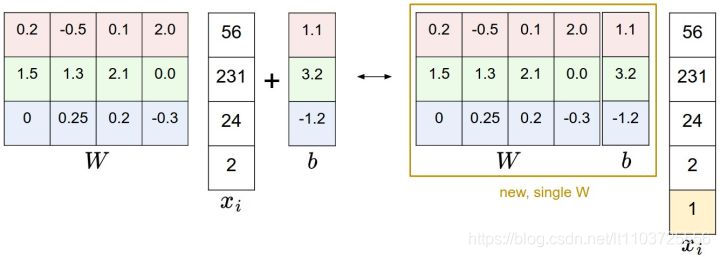
$W^{T}x+b$，这样的话就要更新W矩阵和b向量，我们可以直接把W和b合并，然后给$x$增加一个1，这样原式就变成了$合并后的矩阵\times x$，更新时只用更新一个矩阵就好了，不过缺点是x和w都要增加一个维度，W增加的是b，x增加的是1

零均值中心化

就是每个图像减去所有图像的均值，让每个像素点的范围保持在-127~127