Java中的队列操作与二叉树的广度优先搜索应用-优快云博客

本文链接：https://blog.youkuaiyun.com/ls158390/article/details/129332141

一、在Java中，队列是一个定义了插入和删除操作的接口Queue
常用操作为：

操作	抛异常	不抛异常
插入元素	add(e)	offer(e)
删除元素	remove	poll()
返回最前面的元素	element	peek()

通常使用不抛出异常的函数
在Java中实现了接口Queue的常用类型有LinkedList、ArrayDeque、PriorityQueue等。但PriorityQueue并不是真正的队列。
41-滑动窗口的平均值
在这里插入图片描述
解题思路：利用队列先进先出的特点，当队列满了的时候优先删除队头元素

class MovingAverage {

    /** Initialize your data structure here. */
    public Queue<Integer> nums;
    public int cap;
    public int sum=0;//定义全局变量,sum具有累加效应

    public MovingAverage(int size) {
        nums=new LinkedList<>();
        cap=size;
    }
    
    public double next(int val) {
        nums.offer(val);//元素入队列
        sum+=val;
        if(nums.size()>cap){
            sum-=nums.poll();//元素出队列
        }
        return (double)sum/nums.size();
    }
}

二、通常基于队列来实现二叉树的广度优先搜索
二叉树的广度优先搜索是从上到下按层遍历二叉树。
从二叉树的根节点开始，先把根节点放入一个队列之中，然后每次从队列中取出一个节点遍历。如果该节点有左右子节点，则分别将它们添加到队列当中。
经典代码如下：

 public class TreeNode{
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {}
        TreeNode(int val) {this.val=val;}
        TreeNode(int val,TreeNode left,TreeNode right){
            this.val=val;
            this.left=left;
            this.right=right;
        }
    }
    //用队列实现二叉树的广度优先搜索
    public List<Integer> bfs(TreeNode root){
        Queue<TreeNode> queue=new LinkedList<>();
        if(root!=null){
            queue.offer(root);
        }
        List<Integer> result=new ArrayList<>();
        while(!queue.isEmpty()){
            TreeNode node=queue.poll();//节点出队列
            result.add(node.val);
            if(node.left!=null){
                queue.offer(node.left);
            }
            if(node.right!=null){
                queue.offer(node.right);
            }
        }
        return result;
    }

43-在完全二叉树中添加节点

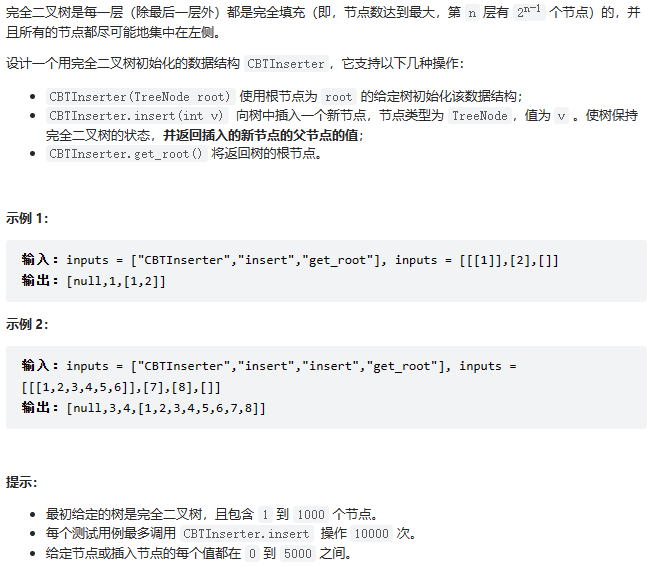
在这里插入图片描述
解题思路：
树是由结点或顶点和边组成的(可能是非线性的)且不存在着任何环的一种数据结构。没有结点的树称为空(null或empty)树。一棵非空的树包括一个根结点，还(很可能)有多个附加结点，所有结点构成一个多级分层结构。
完全二叉树：一棵深度为k有n个节点的二叉树，对树中的节点按从上至下、从左至右的顺序进行编号，如果编号为i(1<=i<=n)的节点与满二叉树中编号为i的节点在二叉树中位置相同。

在完全二叉树中添加新节点顺序看起来是从上到下按层从左到右添加的，这就是典型的二叉树广度优先搜索的顺序。
关于效率优化问题，没有必要在每次插入新的节点都从根节点开始从头进行广度优先搜索。

while(queue.peek().left!=null&&queue.peek().right!=null){
            TreeNode node=queue.poll();//若一个节点的左右孩子不为空，那么在队列中删除该节点，并让该节点的左右孩子入队列
            queue.offer(node.left);
            queue.offer(node.right);
        }

这一步代码是为了让有左右孩子的父节点不入队列，而它的左右孩子入队列，反复筛选，那么队首的元素就为第一个缺孩子的节点。
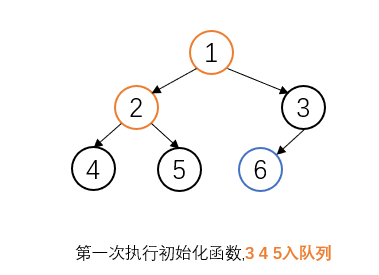
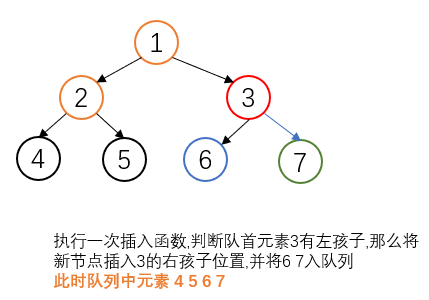
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class CBTInserter {
    Queue<TreeNode> queue;
    TreeNode root;

    //初始化
    public CBTInserter(TreeNode root) {
        this.root=root;

        queue=new LinkedList<>();
        queue.offer(root);
        while(queue.peek().left!=null&&queue.peek().right!=null){
            TreeNode node=queue.poll();//若一个节点的左右孩子不为空，那么在队列中删除该节点，并让该节点的左右孩子入队列
            queue.offer(node.left);
            queue.offer(node.right);
        }
    }

    //插入一个节点
    public int insert(int v) {
        TreeNode parent=queue.peek();//parent已经记录队列中最前面的值（作为父节点）
        TreeNode node=new TreeNode(v);

        if(parent.left==null){
            parent.left=node;
        }else{
            parent.right=node;//一个节点的左右孩子不为空，那么在队列中删除该节点，并让该节点的左右孩子入队列

            queue.poll();
            queue.offer(parent.left);
            queue.offer(parent.right);
        }
        return parent.val;
    }
    
    public TreeNode get_root() {
        return this.root;

    }
}

44-二叉树每层的最大值
在这里插入图片描述

第一种：设置两个队列，第一个队列存放当前节点，第二个队列存放下一层节点，当第一个队列节点为空时，第一个队列置换成第二个队列，第二个队列清空。
代码如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> largestValues(TreeNode root) {
        Queue<TreeNode> queue1=new LinkedList<>();//存放当前层的节点
        Queue<TreeNode> queue2=new LinkedList<>();//存放下一层的节点
        List<Integer> result=new LinkedList<>();
        if(root!=null){
            queue1.offer(root);
        }
        int max=Integer.MIN_VALUE;
        while(!queue1.isEmpty()){
            TreeNode node=queue1.poll();
            max=Math.max(max,node.val);
            if(node.left!=null){
                queue2.offer(node.left);
            }
            if(node.right!=null){
                queue2.offer(node.right);
            }
            if(queue1.isEmpty()){
                queue1=queue2;//queue1指向queue2
                queue2=new LinkedList<>();//queue2队列的值清空
                result.add(max);
                max=Integer.MIN_VALUE;
            }
        }
        return result;   
    }
}

第二种思路：用两个变量current和next标记当前层和下一层

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> largestValues(TreeNode root) {
        int current=0;//记录当前层的节点个数
        int next=0;//记录下一层的节点个数
        Queue<TreeNode> queue=new LinkedList<>();
        List<Integer> result=new LinkedList<>();
        
        if(root!=null){
            queue.offer(root);
            current=1;
        }
        int max=Integer.MIN_VALUE;
        while(!queue.isEmpty()){
            current--;
            TreeNode node=queue.poll();
            max=Math.max(max,node.val);
            if(node.left!=null){
                next++;
                queue.offer(node.left);
            }
            if(node.right!=null){
                next++;
                queue.offer(node.right);
            }
            if(current==0){
                current=next;
                next=0;
                result.add(max);
                max=Integer.MIN_VALUE;
            }
        }
        return result;
    }
}

45-二叉树最底层最左边的值
在这里插入图片描述
解题思路：根据44题的改编，记录最底层最左边的节点，可以让队列1每次出栈队首元素就是每一层最左边的元素。

class Solution {
    public int findBottomLeftValue(TreeNode root) {
    
        Queue<TreeNode> queue1=new LinkedList<>();//队列1记录当前节点信息
        Queue<TreeNode> queue2=new LinkedList<>();//队列2记录下一层节点信息 
        int num=root.val;
        queue1.offer(root);
        while(!queue1.isEmpty()){
            TreeNode node=queue1.poll();
            if(node.left!=null){
                queue2.offer(node.left);
            }
            if(node.right!=null){
                queue2.offer(node.right);
            }
            if(queue1.isEmpty()){
                queue1=queue2;//当队列1为空时，队列1=队列2
                queue2=new LinkedList<>();//队列2清空，为了记录下一层节点信息 
                if(!queue1.isEmpty())
                num=queue1.peek().val;
            }
        }
        return num;
    }
}

46-二叉树的右侧视图
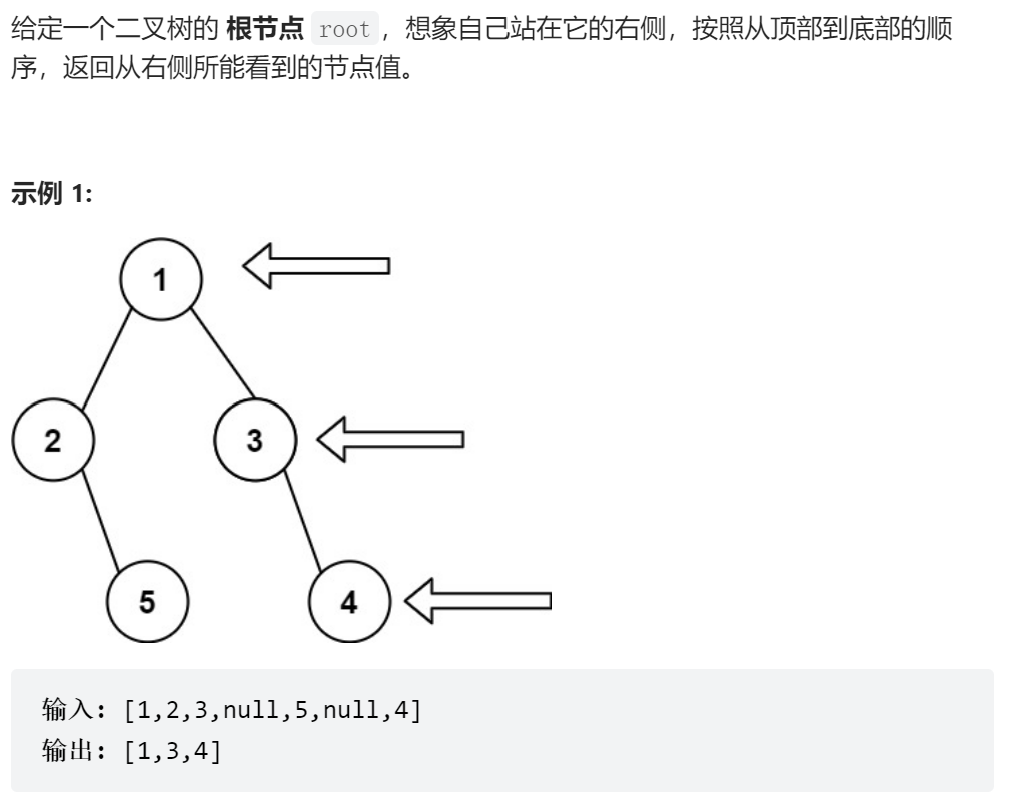
在这里插入图片描述
解题思路：根据第44题的改编，可以理解为每一层最右边的节点，也就是说当队列1（当前节点集合）为空时，记录最后一次出栈的节点值。

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        Queue<TreeNode> queue1=new LinkedList<>();
        Queue<TreeNode> queue2=new LinkedList<>();
        List<Integer> result=new LinkedList<>();

        if(root==null){
            return result;
        }

        queue1.offer(root);
        while(!queue1.isEmpty()){
            TreeNode node=queue1.poll();
            if(node.left!=null){
                queue2.offer(node.left);
            }
            if(node.right!=null){
                queue2.offer(node.right);
            }
            if(queue1.isEmpty()){
                result.add(node.val);
                queue1=queue2;
                queue2=new LinkedList<>();
            }
        }
        return result;
    }
}

47-二叉树剪枝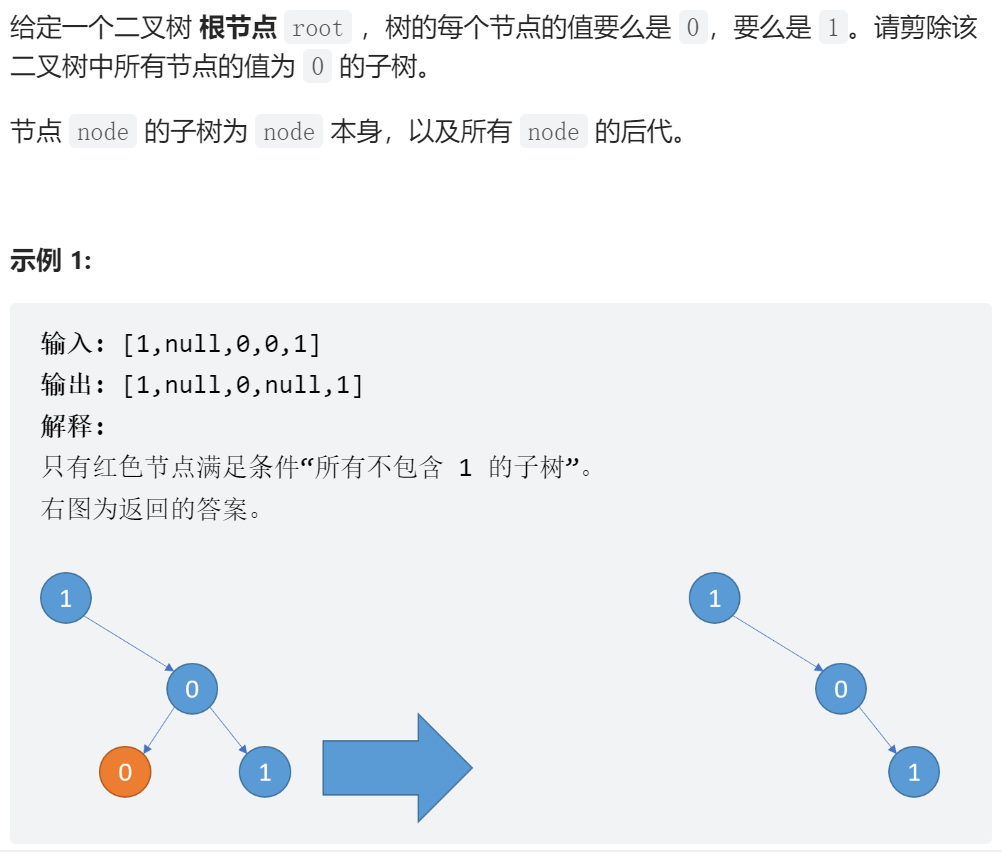在这里插入图片描述
解题思路：利用树后序遍历（左右根）的思想，先递归删除左右子树节点值全为0的节点，然后再判断当点节点左右子树节点全为空，且当前节点值为0时，这个节点才能删除。

class Solution {
    public TreeNode pruneTree(TreeNode root) {
        if(root==null){
            return root;
        }
        //利用后序遍历的思想
        root.left=pruneTree(root.left);//先递归删除左右子树节点值全为0的子树
        root.right=pruneTree(root.right);
        if(root.left==null&&root.right==null&&root.val==0){
        //当root左右子树全为空，并且它的值也为0时，这个节点才能被删除
            return null;
        }
        return root;
    }
}

队列的基本知识