一、654.最大二叉树
又是构造二叉树,昨天大家刚刚做完 中序后序确定二叉树,今天做这个 应该会容易一些, 先看视频,好好体会一下 为什么构造二叉树都是 前序遍历题目链接/文章讲解:代码随想录
1. 整体思路
(1)递归终止条件:当传入的数组大小等于1,说明到达叶子节点,停止递归。由于题目中已经定义数组的大小大于等于1,所以不需要对空数组的情况进行处理。
(2)定义一个maxvalue用于更新数组最大值,找到中间结点;同时需要定义一个index用于更新当前数组最大值的下标,只有找到最大值的下标才可以切分数组。由于题目要求数组所有数字均为正整数,所以此处maxvalue初始化为0,最大值下标index也初始化为0。
(3)给定数组来构造二叉树必须使用中序遍历,因为必须先确定中间结点才能进行下一层的树构造。注意:区间均是左闭右开原则。
1)中间节点:遍历数组所有元素,如果有比maxvalue更大的元素,就将该元素的值赋给maxvalue,并且将该元素的下标传递给index。接下来定义新节点,传入maxvalue。
2)左子树:向左遍历递归构造左子树,必须保证左区间的元素个数一定需要大于等于1,所以限制条件index大于0,就可以构建左子树, 从而进行切割新数组。
3)左子树:index<nums.size-1保证分割点的右区间的大小一定是大于等于1的,接下来同样分割左右区间。
(4)将节点返回。
(5)优化:每一步构造新数组比较耗时,可以进行合并优化。
2. 完整代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
# 递归的终止条件:遍历至叶子节点则停止递归
if len(nums) == 1:
return TreeNode(nums[0])
# middle:
max_value = 0 # 初始化最大值
index = 0 #初始化最大值下标
for i in range(len(nums)):
if nums[i] > max_value:
max_value = nums[i]
index = i
node = TreeNode(max_value) # 更新定义中间节点
# left:
if index > 0: # 递归前,需要确保切割点的左区间元素大于等于1
nums_left = nums[: index]
node.left = self.constructMaximumBinaryTree(nums_left) # 递归左子树
# right:
if index < len(nums)-1: # 递归前,需要确保切割点的右区间元素大于等于1
nums_right = nums[index+1: ]
node.right = self.constructMaximumBinaryTree(nums_right) # 递归右子树
return node
二、617.合并二叉树
这次是一起操作两个二叉树了, 估计大家也没一起操作过两个二叉树,也不知道该如何一起操作,可以看视频先理解一下。 优先掌握递归。题目链接/文章讲解:代码随想录
1. 整体思路
(1)确定函数返回值和传入参数:函数返回值为合并后二叉树的根节点,传入参数为待合并两个树的根节点。
(2)确定终止条件:要明确的是tree1和tree2是同步遍历的,所以当遍历到tree1某节点为空时,返回tree2(此时tree2也遍历到同一位置节点);当遍历到tree2某节点为空时,返回tree1(此时tree1也遍历到同一位置节点)。不需要考虑tree1和tree2同时为空的情况,因为上述条件已经包含了tree1和tree2同时为空,会自动返回null。
以上两种情况考虑后,如果tree1和tree2都不为空,那么将tree1和tree2对应位置上的值直接相加。
(3)单层递归逻辑:分别递归左右子树。
(4)返回根节点。
(5)此外,本题可以在tree1或tree2基础上修改,或者定义新树;本题前中后序遍历均可。

2. 完整代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
# middle:
if not root1:
return root2
if not root2:
return root1
root1.val += root2.val
# left:
root1.left = self.mergeTrees(root1.left, root2.left)
# right:
root1.right = self.mergeTrees(root1.right, root2.right)
return root1三、700.二叉搜索树中的搜索
递归和迭代 都可以掌握以下,因为本题比较简单, 了解一下 二叉搜索树的特性题目链接/文章讲解: 代码随想录
1. 搜索树的特性
二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
2. 递归法代码
(1)首先函数的返回值是节点指针,传入的参数是二叉搜索树和目标值。判断传入的节点是否为空,如果为空,直接返回根节点。
(2)如果目标值小于当前中间节点值,那么根据搜索二叉树的特性,要搜索的节点一定在当前节点的左子树中,所以必须向左子树去遍历。
(3)如果目标值大于当前中间节点值,那么根据搜索二叉树的特性,要搜索的节点一定在当前节点的右子树中,所以必须向右子树去遍历。
(4)如果没有搜索到结果,自动默认返回null。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root or root.val == val:
return root
result = TreeNode(val = None)
if val < root.val:
result = self.searchBST(root.left, val)
if val > root.val:
result = self.searchBST(root.right, val)
return result四、98.验证二叉搜索树
遇到 搜索树,一定想着中序遍历,这样才能利用上特性。但本题是有陷阱的,可以自己先做一做,然后在看题解,看看自己是不是掉陷阱里了。这样理解的更深刻。
题目链接/文章讲解:代码随想录
1. 二叉搜索树的特性
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
2. 直白想法
利用二叉搜索树的特性,采用中序遍历(左中右),遍历树,并存放在数组中,如果数组排列从小到大,那么说明这棵树是搜索二叉树。
3. 递归法代码误区
仅比较中间节点比左孩子大且比右孩子小,然而二叉搜索树需要满足中间节点比左子树上所有节点值大且比右子树所有节点值小。
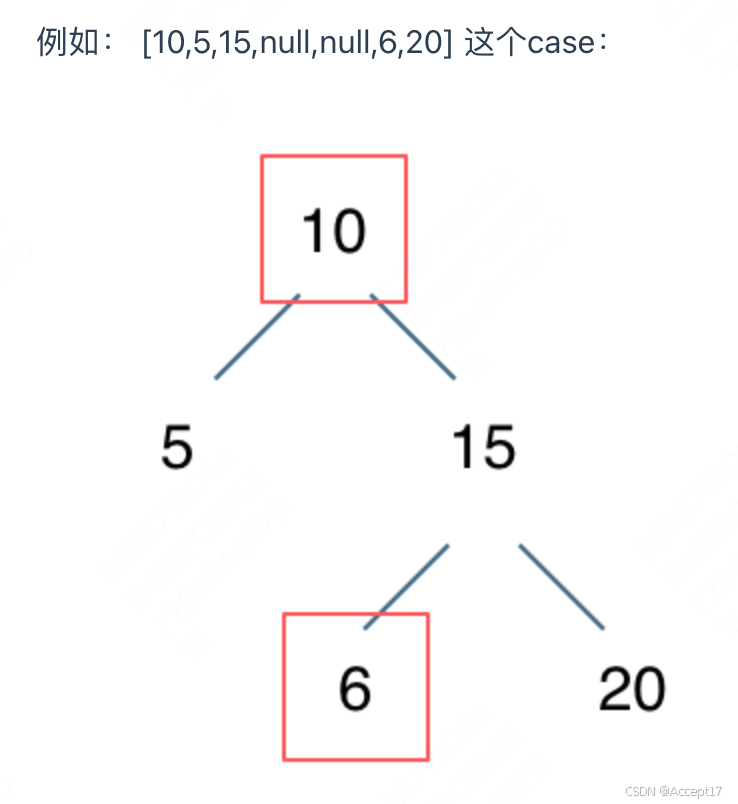
4. 代码实现
(1)本题采用中序遍历,用于比较中间节点是否大于左子树所有节点,并且小于右子树所有节点。递归函数的返回值为bool类型,传入参数为根节点。如果根节点为空,那么返回true,因为空树是满足所有类型的树的条件的。
(2)定义maxvalue,初始化为最小值。这样在第一次比较时,中间节点一定比maxvalue小,完成maxvalue的第一次更新,便于后续递归。
(3)首先向左去递归遍历,然后中间节点比较和maxvalue的大小,如果中间节点大于maxvalue,那么更新maxvalue的值为当前中间节点的值,如果中间节点小于等于maxvalue,那么直接返回false,说明并不是左子树的所有节点都小于中间节点。最后递归遍历右子树。
(4)最后如果左右遍历均满足条件则返回true。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.max_value = float('-inf')
def isValidBST(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
left = self.isValidBST(root.left)
if self.max_value < root.val:
self.max_value = root.val
else:
return False
right = self.isValidBST(root.right)
return left and right




















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








