IJRR’24&RSS‘23 Diffusion Policy Visuomotor Policy Learning via Action Diffusion

0 引言

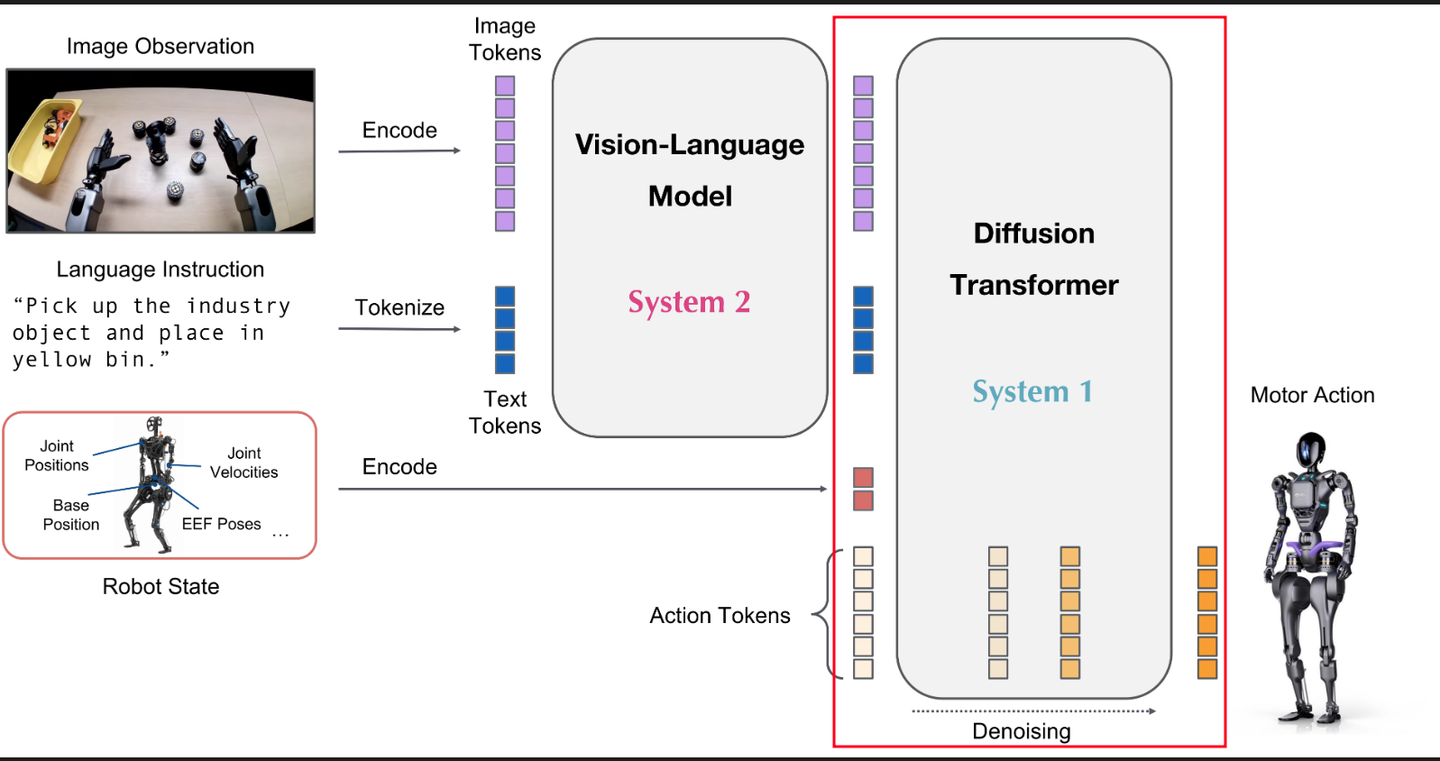
为什么很多vla的动作输出头都是用扩散策略呢，这大概是来源于一篇很重要的论文Diffusion Policy: Visuomotor Policy Learning via Action Diffusion.

1 简介

本文介绍了Diffusion Policy，一种通过条件去噪扩散过程表示机器人视觉运动策略的新方法。在4个不同机器人操作基准的15个任务中，Diffusion Policy consistently outperforms existing state-of-the-art methods，平均性能提升46.9%。该方法学习行动分布分数函数的梯度，并通过随机朗之万动力学步骤在推理期间优化该梯度场。

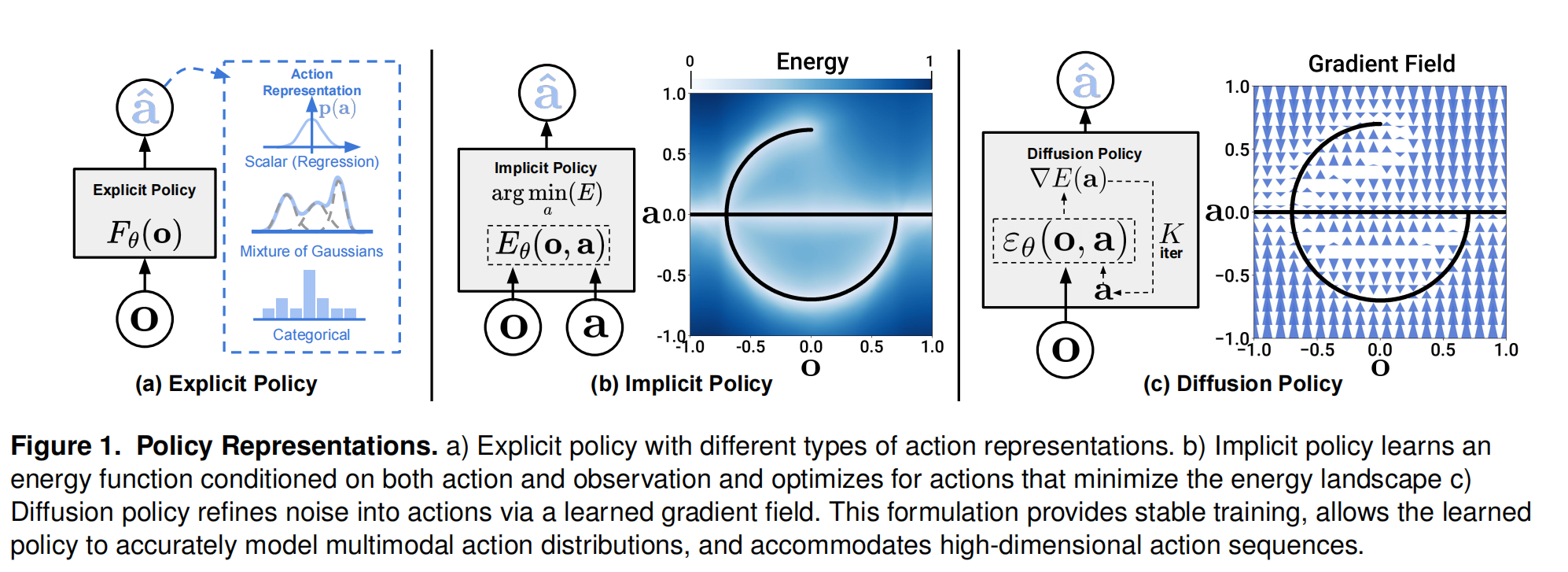
与显式策略（相当于直接学习一个状态到动作的映射函数/控制器）和隐式策略（相当于学习一个关于观测和动作的能量/评价函数，引导策略向能量最小的地方去，类似Q学习和D学习）不同，扩散策略学习一个将噪声引导至动作的向量场，这样的方式能够使模型准确的对多模态动作分布进行建模，并适应高维动作序列。

2 Diffusion Policy Formulation

2.1 DDPM

生成过程被视为从高斯噪声开始的迭代去噪（Stochastic Langevin Dynamics）。
核心公式：$x^{k-1}=\alpha (x^k-\gamma {ϵ}_{\theta }(x^k,k)+N(0,{\sigma }^{2}I))$
上述公式也可以用一个简单的噪声梯度下降代替：$x^{\prime }=x-\gamma \nabla E(x)$
其中，噪声预测网络${ϵ}_{\theta }(x^k,k)$用来预测梯度场$\nabla E(x)$，$\gamma$是学习率

2.2 DDPM训练过程

训练过程从抽取未加噪声的样本开始$x^0$，然后选择去噪的第k次迭代的噪声${ϵ}^k$，噪声预测网络的训练目标函数为：
$L=MSE({ϵ}^k,{ϵ}_{\theta }(x^0+{ϵ}^k,k))$
噪声预测网络${ϵ}_{\theta }$的输入为加噪k步之后的数据$x^k=x^0+{ϵ}^k$和去噪迭代步数k，${ϵ}_{\theta }$旨在预测添加到 $x^0$ 中的噪声

2.2.1 细节描述

${ϵ}^k$被定义为在第 k 次去噪迭代中添加的高斯噪声
${ϵ}^k\sim N(0,{\sigma }_k^{2}I)$
其中方差${\sigma }_k$是一个依赖于当前去噪迭代步数k的值，由噪声调度决定。
噪声调度是扩散模型的核心设计之一，它定义了方差如何随着去噪步数的变化而变化。

2.2.2 噪声调度

噪声调度是一组预定义的参数，用于控制扩散过程中每一步的噪声水平。它不仅仅是定义方差 ${\sigma }_k^2$​，通常还关联着另外两个关键参数 ${\alpha }_k$和 ${\gamma }_k$​。这些参数都是迭代步 k的函数。

• ​​${\sigma }_k^2$​​​：​添加的噪声方差。它决定了在第 k步时，向数据中添加的噪声的强度。
• ​​${\alpha }_k$​​​：​保留信号的比例因子。它控制着在去噪步骤中保留多少上一步的信号。
• ​${\gamma }_k$ ：​梯度步长的学习率。它控制了根据预测的梯度（噪声）更新当前值的步长大小。
• $x^{k-1}=\alpha (x^k-\gamma {ϵ}_{\theta }(x^k,k)+N(0,{\sigma }^{2}I))$ ：这个公式可以理解为：新的、更干净的估计 $x_{k-1}$是由上一轮估计$x_k$的衰减值，减去一个基于预测梯度的修正项，再加上一个小的随机噪声扰动构成的。噪声调度就是为每一步 k定义 $({\alpha }_k,{\gamma }_k,{\sigma }_k)$这个三元组。

2.3 DDPM推理过程

• ​初始噪声采样​：从标准高斯分布中采样一个初始噪声作为起点，可以将其理解为 ${\epsilon }^k$，但此时方差 ${\sigma }_k^2$通常被设置为1（或接近1），因为这是噪声最大的状态。
• 迭代去噪：执行$x^{k-1}=\alpha (x^k-\gamma {ϵ}_{\theta }(x^k,k)+N(0,{\sigma }^{2}I))$，在每一步去噪中，​会重新注入一个方差更小的新噪声。这样做是为了防止结果收敛到一个单一的模（mode），从而保持生成动作的多模态性。

2.4 Diffusion for Visuomotor Policy Learning

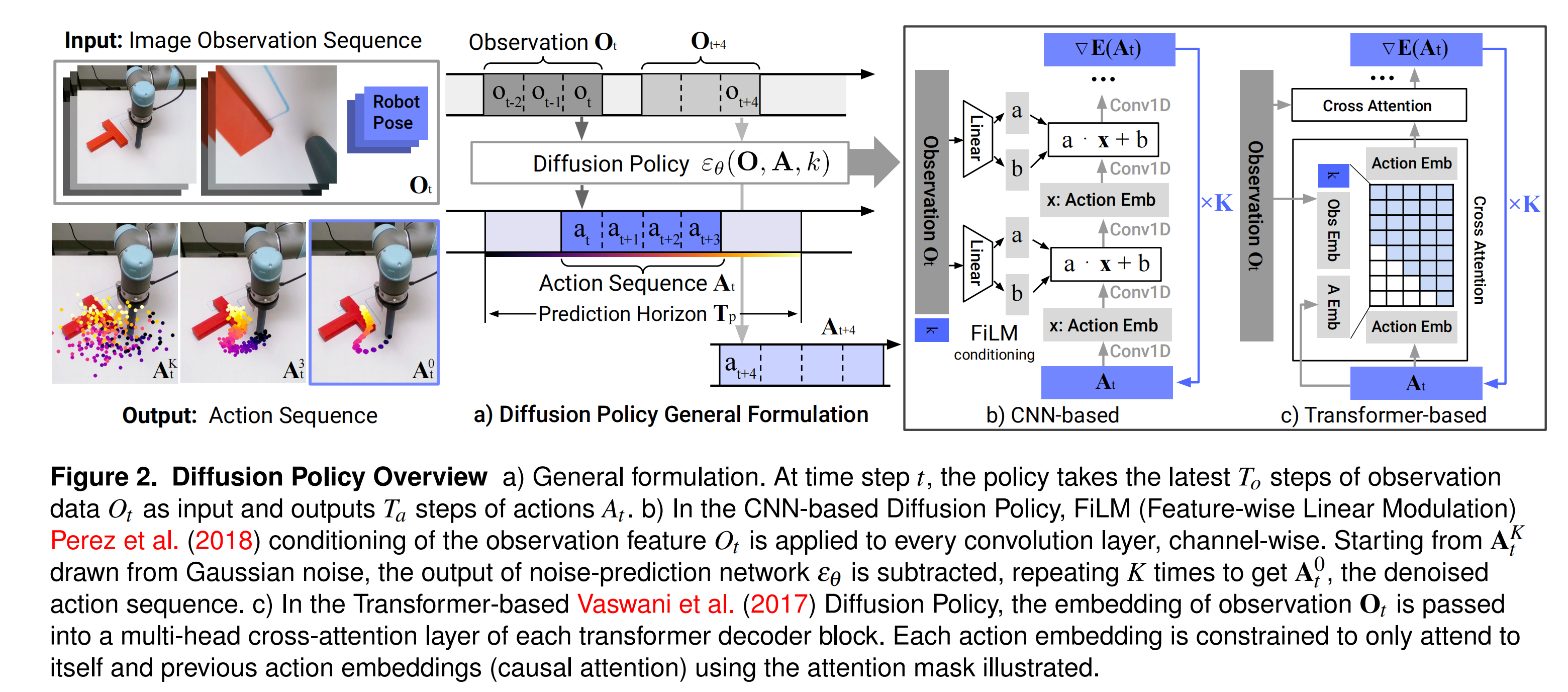
将DDPM应用于视觉运动策略学习，主要修改包括：输出改为机器人动作序列，并引入观察条件化。公式修改为
$A_t^{k-1}=\alpha (A_t^k-\gamma {ϵ}_{\theta }(O_t,A_t^k,k)+N(0,{\sigma }^{2}I))$
目标函数为
$L=MSE({ϵ}^k,{ϵ}_{\theta }(O_t,A_t^0+{ϵ}^k,k))$

3 实现细节

3.1 网络结构

在这里主要讨论了两种去噪网络的结构选用，分别是CNN和Transformer，主要核心在于如何引入观测条件化

3.1.1 CNN-based

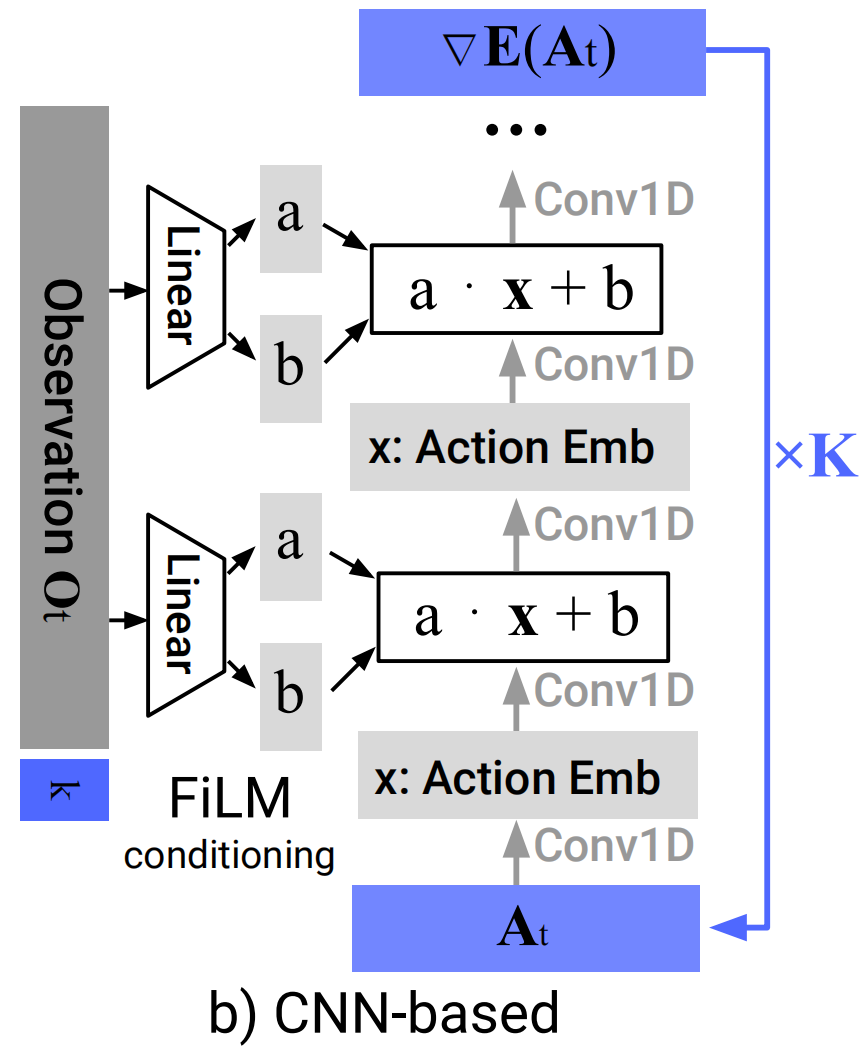
• ​backbone​：使用一个1D时序卷积神经网络。该网络将整个动作序列 $A_t^k$（形状为预测视野×动作维度）视为一个时间序列进行处理。
• ​条件化方式​：采用 ​FiLM（Feature-wise Linear Modulation）​。这是该实现的一个关键设计。FiLM机制在每一个卷积层之后、激活函数之前发生作用。
  • ​过程​：视觉观察 $O_t$（已经通过编码器处理，现在是个紧凑特征向量）通过一个投影网络（如MLP）生成一组FiLM参数（$\gamma$和 $\beta$）。然后，这些参数被应用到CNN的每一个卷积层上，对每个通道的特征图（当前卷积层输出）进行缩放和偏移$(\gamma \cdot F+\beta )$。
  • ​优势​：实现了深度条件化，视觉信息从网络底层到顶层持续引导去噪过程，且计算高效（观察只需编码一次，用于所有去噪迭代）。

3.1.2 Transformer-based

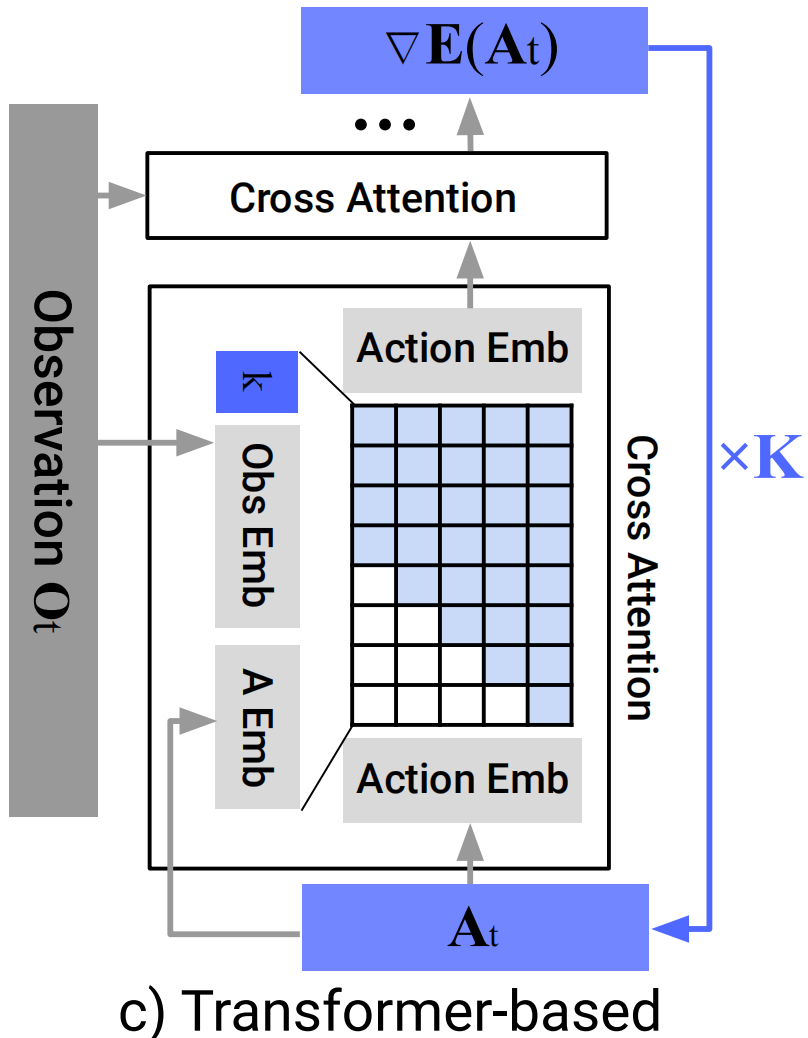
• backbone​：采用Transformer解码器架构​（类似minGPT）。噪声动作序列$A_t^k$​被切分成多个时间步的token，每个token被嵌入后输入Transformer块。
• ​条件化方式​：采用交叉注意力（Cross-Attention）​。
  • ​过程​：视觉观察 $O_t$​被编码为一个序列的嵌入。在Transformer的每一层中，​动作token作为Query，​观察嵌入作为Key和Value，进行多头交叉注意力计算。这使得每个动作token都可以动态地关注观察序列中最相关的部分。
• ​因果注意力掩码​：为确保自回归特性，对注意力矩阵应用因果掩码，使每个动作token只能关注自身及之前的时间步，防止信息泄露。

3.1.3 方式对比

特性	基于CNN的实现	基于Transformer的实现
​核心机制​	1D时序卷积	Transformer解码器 + 因果注意力
​条件化方式​	​FiLM​：深层、逐层特征调制	​交叉注意力​：动态、基于内容的查询
​训练稳定性​	​高，开箱即用，超参数鲁棒	​相对敏感，需要更多调优
​处理高频动作​	较弱，存在过度平滑效应	​强，能捕捉快速变化
​计算效率​	通常更高，推理速度更快	参数更多，计算量可能更大
​推荐场景​	大多数任务的首选起点，尤其是动作变化平滑的任务	任务复杂、动作变化剧烈，且CNN性能不足时

3.2 视觉编码器

视觉编码器的主要作用是将图像编码为高维隐空间特征$O_t$，在这里使用未经过预训练的ResNet-18架构，通过端到端训练提取视觉特征。

3.3 噪声调度

采用Square Cosine Schedule，控制扩散过程的学习率调度，以平衡高低频动作信号。
平方余弦调度能更平滑地过渡不同噪声水平，通常比线性调度表现更好。

3.4 现实中的推理加速

使用DDIM（Denoising Diffusion Implicit Models）减少去噪迭代次数，实现实时控制。

4 扩散策略中的有趣特性

4.1 建立动作的多模态分布

在模仿学习的行为克隆中，对多模态分布的建模一直是个难题。但是扩散策略可以很好的解决。
扩散策略在动作生成中的多模态特性源自两个核心要素：

• 底层随机采样机制与随机初始化过程。具体而言，在随机朗之万动力学框架中，每次采样开始时都会从标准高斯分布中抽取初始样本$A_t^k$，这为最终动作预测$A_t^0$设定了不同的收敛区域。
• 通过大量迭代中的高斯扰动优化，即去噪过程中加入的高斯噪声，使得各个动作样本既能收敛又能自由穿梭于不同多模态的行动空间。
  

4.2 位置控制

文章中对比了几种方法在速度控制和位置控制中表现的异同。传统方法通常在位置控制中表现打折扣，但是扩散策略更适合于位置控制模式。Diffusion Policy恰好能够克服位置控制的传统缺陷（多模态性）​，并充分利用其固有优势（无漂移）​，而其他方法则不能。

4.3 动作序列预测

Diffusion Policy通过其强大的生成能力，能够有效预测未来多个时间步的动作序列。这种“序列到序列”的映射方式，相比传统的“观察到单步动作”的映射，带来了三大关键优势：

• 提升时序动作一致性
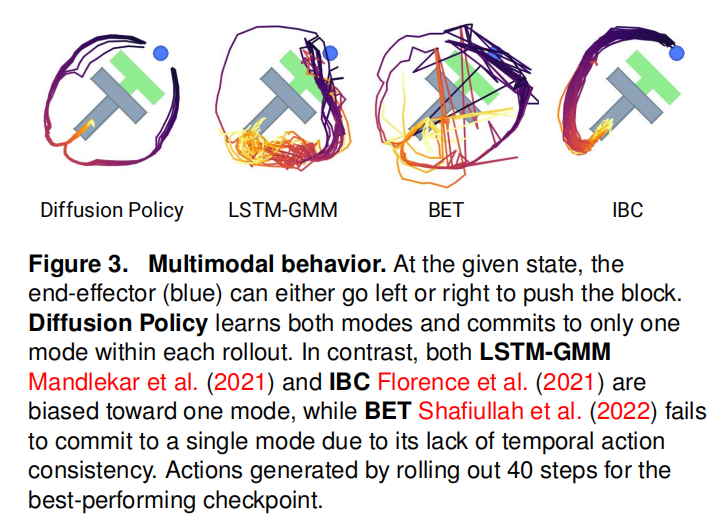
  • ​问题​：在多模态场景中（例如，从左侧或右侧绕过障碍物），如果每一步都独立地从多模态分布中采样， consecutive actions could be drawn from different modes，导致动作抖动、轨迹在两种模式间跳变的不稳定行为。
  • Diffusion Policy的解决方案​：通过一次性预测整个动作序列，Diffusion Policy能够承诺于一个单一的模式。在Push-T任务中，策略在每次 rollout 中都会坚定地选择“从左绕”或“从右绕”的一条轨迹，并执行到底，从而生成平滑、一致、物理上可行的动作。
• 对空闲动作的鲁棒性
  • 问题​：在人类示教数据中，经常存在“空闲动作”（Idle Actions），即操作者暂停时产生的一段位置不变或速度为零的动作序列。单步策略极易过拟合这种暂停行为，导致策略在执行时经常“卡住”。
  • ​Diffusion Policy的解决方案​：通过预测序列，策略能够更好地理解上下文。它能够识别出空闲动作是演示中的一个特殊“段落”，并在生成动作序列时，主动地“跳过”或“填充”上合理的动作，从而避免陷入停滞。
• 减轻累积误差
  • 问题​：在速度控制下，单步预测的微小误差会随时间累积，导致最终位姿严重偏离。
  • ​Diffusion Policy的解决方案​：预测一个绝对位置序列（与位置控制协同）或一个长远的速度序列，能够在规划层面就考虑到整个时间窗口内的动作协调性，从而从根源上减少每一步的决策误差，避免误差累积。

4.4 训练稳定性

Diffusion Policy通过学习梯度函数而非能量函数，规避了估计难以处理的归一化常数这一难题，从而实现了显著优于隐式策略的训练稳定性。这使得它易于调参和部署。

4.5 控制理论的联系

对于一个简单的含有噪声的线性系统：
$s_{t+1}=A{s}_t+B{a}_t+w_t,w_t\sim N(0,{\Sigma }_w)$
假设演示数据是来源于一个LQR控制策略$a_t=-K{s}_t$。

• 收敛性断论：当预测步长为1时，迭代去噪过程，可以看作是在这个简单的凸优化问题（梯度场）上，从随机初始点（噪声）开始，​进行一系列梯度下降步骤。由于问题本身是凸的（线性系统），梯度下降必然会收敛到全局最优点，也就是 $a_t=-K{s}_t$。
• 动力学模型学习：当预测步长大于1时，去噪过程需要产生$a_{t+t^{\prime }}=-K(A-BK{)}^{t^{\prime }}{s}_t$，这展示出为了在未来时刻$t^{\prime }$做出正确的动作 $a_{t+t’}$，策略需要知道到那个时刻的状态会变成什么样子，即隐式的学出了动力学模型。如果模型是非线性并且包含复杂噪声，这将更适合使用扩散策略。

5，6，7为实验分析，待补充