系列第二篇,大致整理一下部分基本概念和引理。
主要是用于笔记和备忘,初稿可能有点乱,后续熟悉后可能会重新整理,如有错误也可评论指出。
目录
一、上溢Overflow
假设“中间结果”定义为:指数范围不限时,经过舍入后的计算结果。当上溢的异常发生时,“中间结果”的绝对值是有限的,但严格大于最大有限规格数;或者说,此时指数严格大于指数最大值
。此时返回的结果取决于舍入方向。
- 对于RN舍入到最近模式(包括roundTiesToEven和roundTiesToAway两种),结果将是
,符号与中间结果一致;
- 对于RZ向零舍入,结果为
,符号与中间结果一致;
- 对于RD向下舍入,若中间结果为正,则返回+
;反之,返回
;
- 对于RU向上舍入,若中间结果为负,则返回-
;反之,返回
;
此外,发生上溢时,不精确计算异常也会触发。
注意!!!!!!!!!!!!!!!:
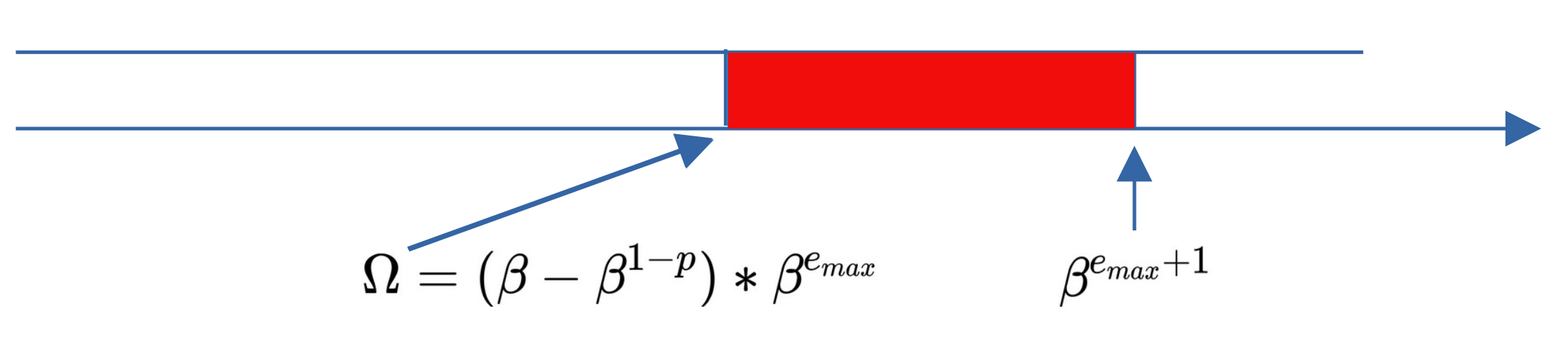
- 对于RN舍入到最近,若某种运算的精确结果绝对值大于等于Ω+1/2 ulp(Ω),即
,超过了最后两个连续有限浮点数的一半,则返回无穷大,这与舍入到最近的字面意思可能不同。
- 上溢不等同于返回无穷大结果。
- 对于RZ,上溢不等同于返回
:若某运算的精确结果的绝对值大于等于Ω、且严格小于
,则返回
,但不发生上溢。
二、下溢Underflow
下溢异常触发时,意味着计算得到了一个非零结果,其绝对值严格小于最小规格数。
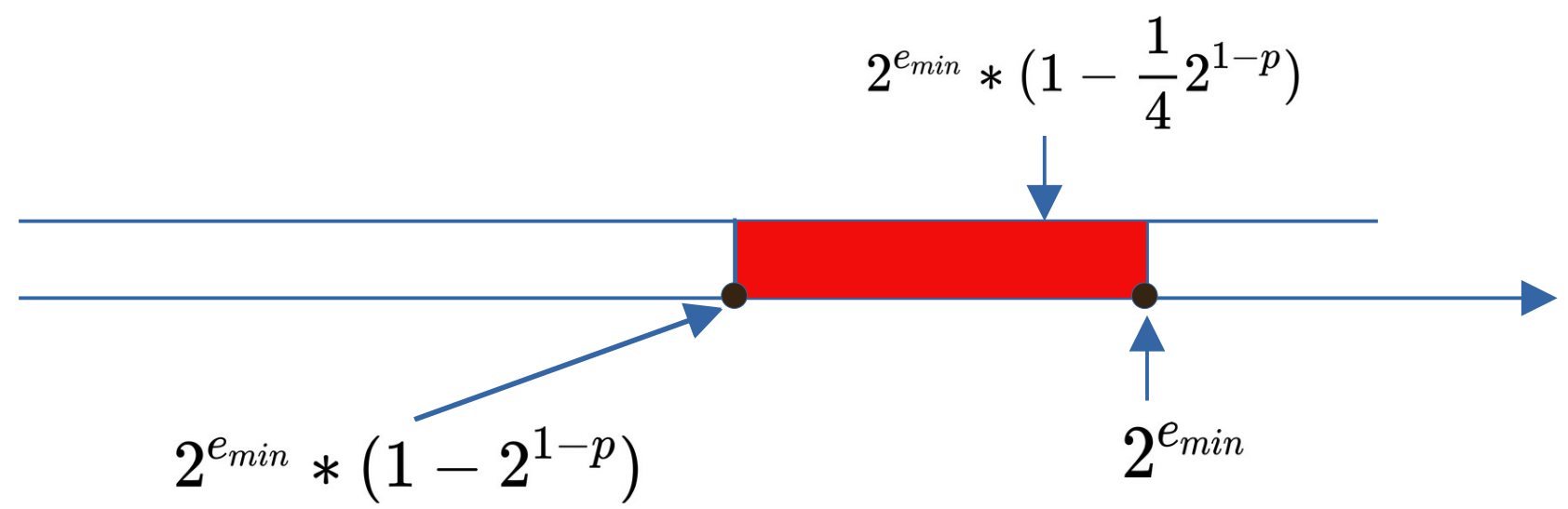
- 对于二进制编码,下溢可能在舍入前发生,即精确结果的绝对值非零且严格小于
。也可能在舍入后发生,即假设指数范围无界时计算得到的非零结果的绝对值严格小于
。在极少情况下会产生影响,如
,使用RN模式,在舍入前检查下溢的话会触发下溢,而在舍入后检查则不会触发下溢。
- 对于十进制编码,下溢结果会在舍入前被检测到并触发。即当下溢的精确结果的绝对值非零且严格小于
时,就会触发下溢异常。
发生下溢时,若结果不精确inexact,置下溢标志的同时会置不精确异常。若结果精确,下溢标志不会被置位。IEEE的解释:下溢标志用于警示某些运算结果的精度可能不高 。因此,当运算精确时置位该标志,就是不必要的警示。后面会提到,根据Hauser定理表明,对于舍入到最近偶数的两种舍入方向属性而言,每当加法或减法发生下溢(即计算结果是subnormal)时,运算结果都是exact精确的。
三、特殊数
1、NaN:Not a Number
signaling NaNs(sNaNs):在默认情况下,不会作为算术结果出现。当 sNaN 参与大多数算术运算时,会触发 无效操作异常(Invalid Operation Exception)。用于调试和显式错误检查,例如检测未初始化的浮点数据。
指数位全为1,尾数最高位为0。
quiet NaNs(qNaNs):静默的 NaN,当出现无效操作时返回,作为操作数时不触发异常,用于传播错误。如qNaN*8、sNaN+5、均返回qNaN。
指数位全为1,尾数最高位为1。
2、零和无穷
零和无穷的算术基本上都符合我们的数学直觉。如,
,
。特殊的
。举个特殊例子:
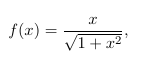
当,这里的
是最大有限浮点数。因此x的平方大于最大有限浮点数,则得到的
将会是
,因此f(x)得到了+0,而实际上x足够大时,可忽略1,f(x)趋近于1。因此对于关键应用,需要提前证明不会发生上溢或下溢,或者通过检查是否发生了溢出。






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










