为什么说kl散度包含ce损失

KL散度（Kullback-Leibler Divergence，简称KL散度）包含交叉熵损失（Cross-Entropy Loss, 简称CE损失）的原因在于它们的数学表达和目标非常相似，且交叉熵损失是KL散度的一部分。我们可以通过它们的公式推导来解释为什么KL散度包含CE损失。

1. 交叉熵损失的定义

交叉熵损失用于度量两个概率分布之间的距离，通常用于分类任务中的目标类别与模型预测概率分布之间的差异。交叉熵损失的公式如下：

其中：

• p(i)p(i)p(i) 是真实标签的概率分布（通常是one-hot编码，正确类别为1，其他类别为0）。
• q(i)q(i)q(i) 是模型的预测概率分布。

交叉熵损失的目标是使模型的预测 q(i)q(i)q(i) 尽可能接近真实分布 p(i)p(i)p(i)。

2. KL散度的定义

KL散度是一种衡量两个概率分布之间差异的度量，通常用于计算一个概率分布相对于另一个分布的"额外"信息。KL散度的公式如下：

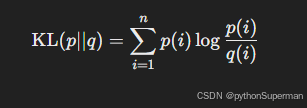
其中：

• p(i)p(i)p(i) 是真实分布（目标分布），
• q(i)q(i)q(i) 是模型的预测分布。

KL散度的目标是衡量模型预测 q(i)相对于真实分布 p(i) 的差异。如果 p(i) 和 q(i) 完全一致，则 KL散度为0。

3. KL散度与交叉熵的关系

KL散度可以拆解为两部分：交叉熵损失和真实分布的熵。我们可以通过公式推导出这种关系：

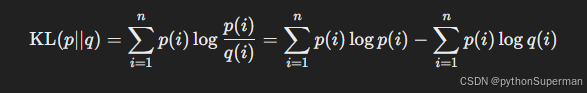
其中：

• 第一项 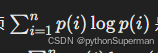是真实分布 ppp 的熵（Entropy）。
• 第二项 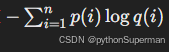是真实分布 p 和预测分布 q之间的交叉熵（Cross-Entropy）。

因此，KL散度可以写成：

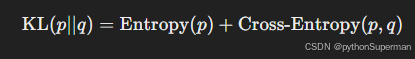
注意，真实分布的熵 Entropy(p)\text{Entropy}(p)Entropy(p) 是一个固定的值，与模型的预测无关。因此，在优化过程中，最小化KL散度实际上等价于最小化交叉熵损失。

4. KL散度包含交叉熵损失的原因

从公式推导可以看出，KL散度实际上是交叉熵损失加上一个常数项（真实分布的熵）。由于真实分布的熵是固定的，因此最小化KL散度与最小化交叉熵损失是等价的。

• 交叉熵损失：度量模型预测与真实分布之间的距离。
• KL散度：在交叉熵损失的基础上，还考虑了真实分布本身的信息量（熵），但这个信息量是固定的。

因此，KL散度包含交叉熵损失，KL散度的最小化过程实际上也在最小化交叉熵损失。

5. 实际应用中的例子

在知识蒸馏中，KL散度常用于将学生模型的预测分布与教师模型的预测分布对齐，因为KL散度能够捕捉到两个概率分布之间的细微差异。而交叉熵损失更多用于将模型的预测与真实标签对齐。

• 知识蒸馏中的KL散度：用于衡量学生模型预测分布和教师模型预测分布之间的差异。
• 分类任务中的交叉熵损失：用于衡量模型预测分布与真实标签之间的差异。

总结

KL散度包含交叉熵损失的原因在于它们的公式结构，KL散度的计算中包含了交叉熵损失部分，加上一个固定的熵项。优化KL散度的过程中，也在优化交叉熵损失。