是否二叉搜索树（注意思路）

题目

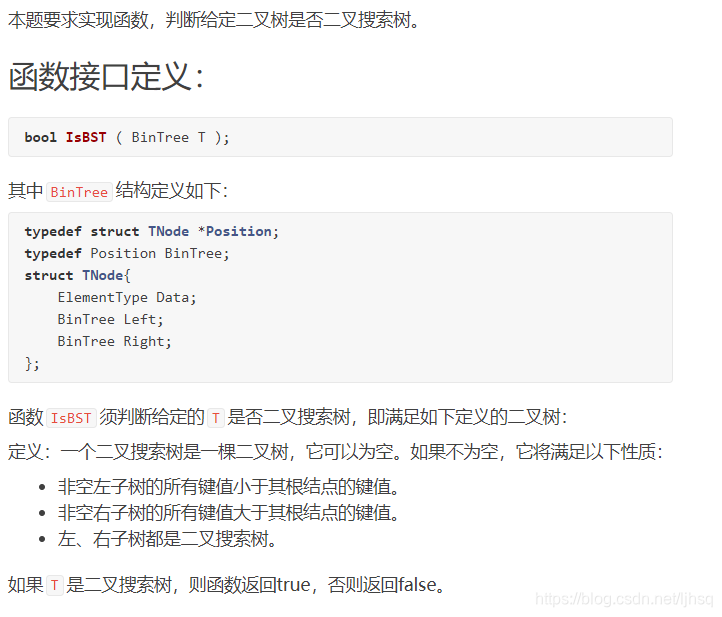
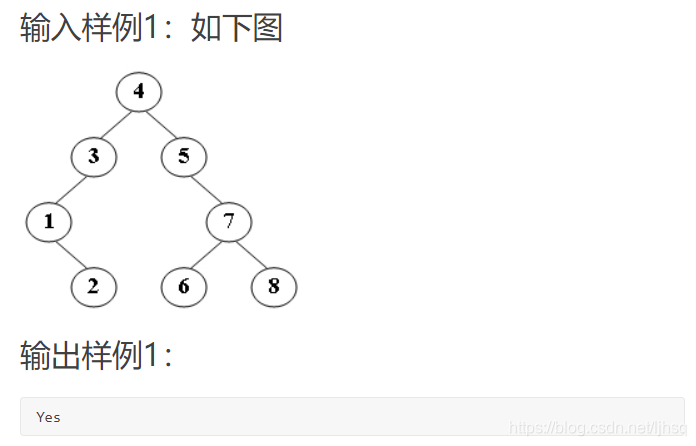
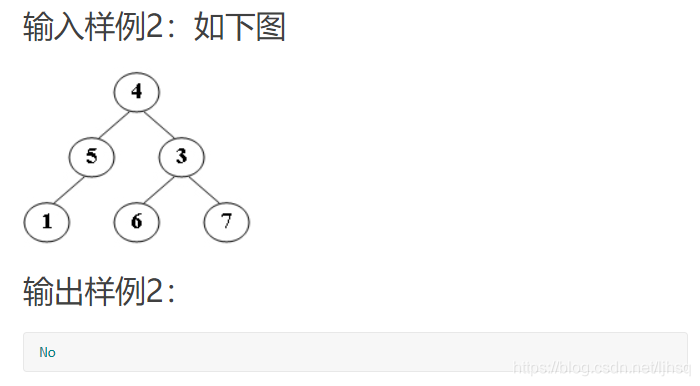
答案

bool IsBST ( BinTree T )
{
	if(!T) return true;
	else if(!T->Left&&!T->Right) return true; 
	BinTree BT1=T->Left,BT2=T->Right;
	if(BT1)
	{
		while(BT1->Right)
		BT1=BT1->Right;
	}
	if(BT2)
	{
		while(BT2->Left)
		BT2=BT2->Left;
	}
	if(BT1->Data<T->Data&&BT2->Data>T->Data) return true;
	else return false;
}

注意

错误思路

刚开始大家很有可能想的是每个节点逐一判断，根据它的左节点，右节点与根节点的关系来判断这个节点是否返回true，但这很明显是错误的。

我举个例子：（画的比较随机，大家见谅哈）

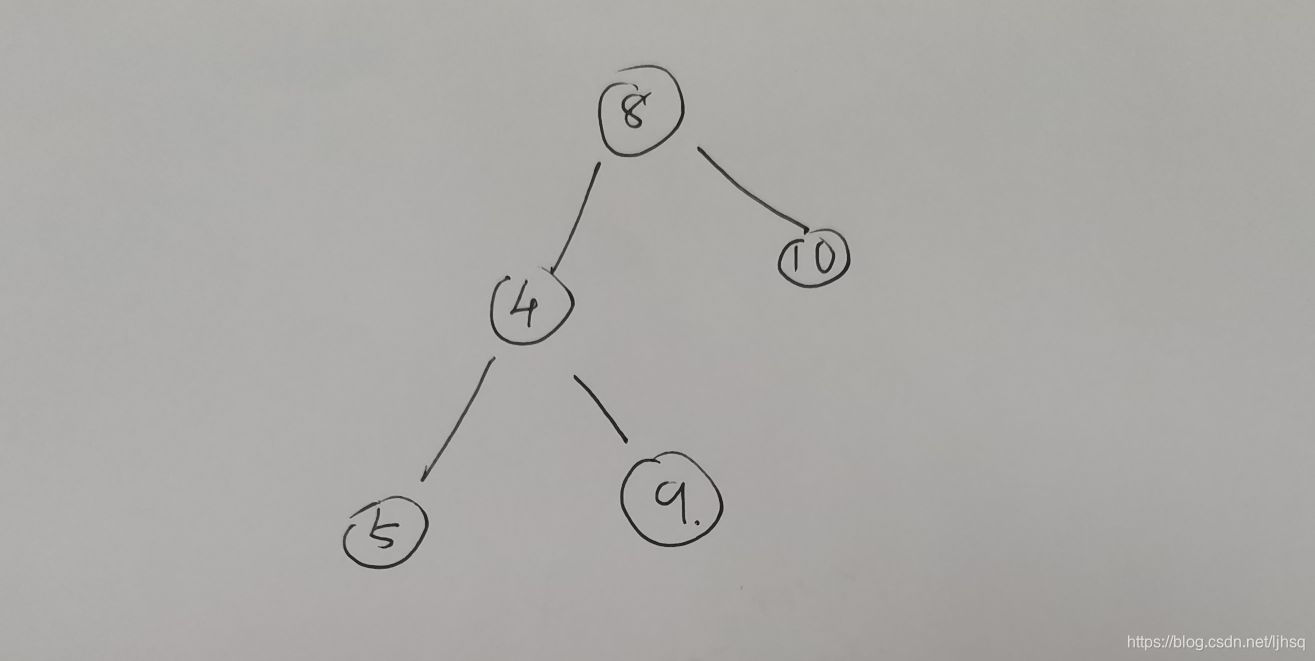
在上图中，根节点（8）的左节点小于8，右节点大于8，但是它的左子树内存在比8大的节点（即9），那么8很明显就不是二叉搜索树

正确思路

因为二叉搜索树要满足“左小右大”的基本原则，所以我们就在根节点的左子树中依次取每一个节点的右子树，直到其为叶节点；同时在根节点的右子树中依次取左子树直至叶节点

这样我们就找到了左侧最大的数以及右侧最小的数，如果左侧最大的数还是比根节点小且右侧最小的数还是比根节点大，那么就一定是二叉搜索树，反之则不是

大家如果觉得这个思路的确有帮助，能不能麻烦大家点上一个免费的赞呢？十分感谢大家！