棋盘覆盖-分治法

在一个 2^k * 2^k 个方格组成的棋盘中，若恰有一个方格与其它方格不同，则称该方格为一特殊方格，称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ，有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。

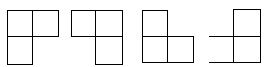
 在棋盘覆盖问题中，要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格，且任何 2 个 L 型骨牌不得重叠覆盖。易知，在任何一个 2^k * 2^k 的棋盘中，用到的 L 型骨牌个数恰为 (4^k-1)/3 。现给出棋盘的大小和特殊方格所在的位置，请找出这种棋盘。

【样例输入】
2

 0 0

【样例输出】
0 1

 1 1

我们在解决此类问题时采用分治方法的将大问题化解成他的子问题。我们可以了解到此方格中每一部分都是2的k次方，都是偶数，而方格往往是奇数，所以我们要将有特殊的区域的方格分隔开例如

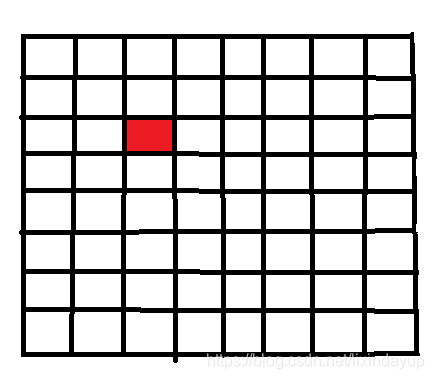
我们将其分割成

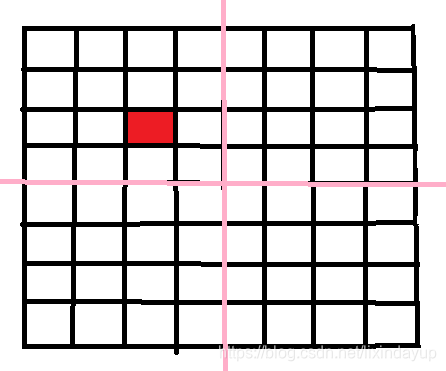
我们需要将其中另外三个转化为奇数个保持稳定

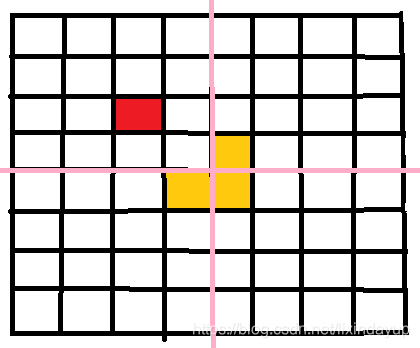
取出四分之一，同样方法


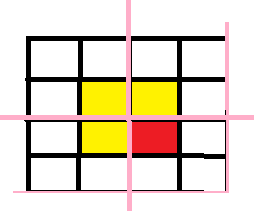
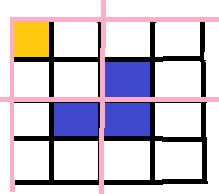
以此类推最终全部变为




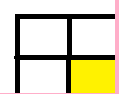
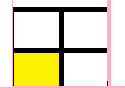
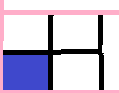
这种类型最终结束调用。
代码如下所示

```cpp
#include<cstdio>
#include<cstring>
int board[17][17]; //初始化棋盘大小 
int tile = 2;	
void show();
void chessBoard(int tr,int tc,int dr,int dc,int size);//初始行列，特殊点行列，棋盘大小 
int main()
{
    memset(board,0,sizeof(board)); //全部填充为零 
    int m,n;
    
    printf("请输入m,n代表该位置初始化为方块\n"); 
	scanf("%d %d",&m,&n);
	board[m][n] = 1;
	
	printf("棋盘覆盖前: \n");
    show();
    chessBoard(1,1,m,n,16);
    printf("\n棋盘覆盖后: \n");
    show();
    return 0;
}
  

 
void show()
{
    for(int i=1;i<=16;i++){
        for(int j=1;j<=16;j++){
            printf("%5d ",board[i][j]);
        }
        printf("\n");
        printf("\n"); 
    }
}
 
void chessBoard(int tr,int tc,int dr,int dc,int size)
{
   if(size==1) return;
 
   int t = tile++;	//L型骨牌号 
   int s = size/2;	//分割棋盘 
 
   		//如果特殊方格在左上角子棋盘，那么覆盖左上角
   if(dr<tr+s && dc<tc+s)
        chessBoard(tr,tc,dr,dc,s);
   else{
        //如果不在，那么填充左上角子棋盘的右下角方格
        board[tr+s-1][tc+s-1] = t;
  		//填充覆盖子棋盘
   		chessBoard(tr,tc,tr+s-1,tc+s-1,s);
   }
 
   		//如果特殊方格在右上角子棋盘，那么覆盖右上角
   if(dr<tr+s && dc>=tc+s)
  		 chessBoard(tr,tc+s,dr,dc,s);
   else{
	   //如果不在，那么填充右上角子棋盘的左下角方格
	   board[tr+s-1][tc+s] = t;
	   //填充覆盖子棋盘
	   chessBoard(tr,tc+s,tr+s-1,tc+s,s);
   }
 
   //如果特殊方格在左下角子棋盘，那么覆盖左下角
   if(dr>=tr+s && dc<tc+s)
   chessBoard(tr+s,tc,dr,dc,s);
   else{
   //如果不在，那么填充左下角子棋盘的右上角方格
   board[tr+s][tc+s-1] = t;
   //填充覆盖子棋盘
   chessBoard(tr+s,tc,tr+s,tc+s-1,s);
   }
 
    //如果特殊方格在右下角子棋盘，那么覆盖左上角
   if(dr>=tr+s && dc>=tc+s)
   chessBoard(tr+s,tc+s,dr,dc,s);
   else{
   //如果不在，那么填充右下角子棋盘的左上角方格
   board[tr+s][tc+s] = t;
   //填充覆盖子棋盘
   chessBoard(tr+s,tc+s,tr+s,tc+s,s);
  }
}