解读分区表的秘密

解读分区表的秘密

2008-07-18 22:50:04

标签： 分区表 MBR CHS LBA

版权声明：原创作品，如需转载，请与作者联系。否则将追究法律责任。

解读分区表的秘密

前几天写了一篇介绍恢复误 Ghost 硬盘的博文，反响出乎意料，很多博友对数据恢复表现出了浓厚的兴趣，希望能对数据恢复作进一步了解。其中大家反映较多的就是希望能看懂分区表的格式，乍一看，由 16 进制数组成的分区表让人望而生畏，如同天书一般。其实，只要理解了分区表参数的含义，天书也就不难读懂了。今天我们就来介绍一下分区表参数，帮助大家掌握分区表。

介绍分区表之前，大家要先准备一些硬盘存储的基础知识，有这么几点：

一 进制转换

分区表中会用到二进制， 16 进制和 10 进制，大家要熟悉它们之间的转换，例如 16 进制的 3F 等于 10 进制的 63 等于二进制的 111111 。好在现在有计算器可以用，心算没把握就用计算器好了，所以进制转换相对不算难。

 

二 常用存储单位

1K ＝ 1024 字节＝ 2¹⁰ 字节

1M ＝ 1024K ＝ 2²⁰ 字节

1G ＝ 1024M ＝ 2³⁰ 字节

1 个扇区＝ 512 字节

介绍这些是因为分区表中表示分区大小是用扇区表示，也就是说分区表中只会说这个分区有多少个扇区，而不会说有多少 G ，多少 M ，因此我们要习惯进行存储单位转换。例如分区表中描述分区大小是 72 A1 A9 03 ，首先你要明白这四个字节是高低位颠倒的，高位在后，低位在前，真正的分区大小是 03 A9 A1 72 。然后我们把 16 进制转为 10 进制，这样就知道了这个分区大小是 61448562 扇区，换算为字节就是 61448562 × 512 ＝ 31461663744 。然后除以 2 的 30 次方，就可以知道分区的大小是 31461663744/ 2³⁰  =29.3 G 。

 

三 扇区定位

硬盘中有数以亿计的扇区，如何才能准确定位到每一个扇区呢？一般用 C/H/S 和 LBA 两种方法。这两种定位方法都很重要，我们来好好看看。

C/H/S 指的是利用柱面 / 磁头 / 扇区这三个参数来定位扇区，有的资料说 C/H/S 指的是磁道，磁头和扇区，这就不准确了。磁道是硬盘盘体上的同心圆，每个磁道上排列了 63 个扇区，盘体最外圈为 0 磁道，从外圈向内圈编号逐步加大。由于一块硬盘有多块盘体，因此硬盘可以看作是一个圆柱体。这时就看出用磁道定位不妥的地方了，磁道显然是只适合在二维空间定位，不适合在三维空间中表示准确的坐标。柱面就没有这个问题了，柱面是所有盘体上磁道的集合，例如 0 柱面指的是所有盘体上的 0 磁道所组成的一个圆柱体。这下您肯定明白了，原来磁道是二维的圆，柱面是三维的圆柱。

一 个柱面包含了若干磁道，如何来准确表示柱面中的具体磁道呢？这时就可以使用磁头参数了。每个磁头负责读取柱面中的处于不同高度的磁道，我们只要给出具体的 磁头数值，就知道对应柱面中的哪个磁道了。这样我们根据柱面和磁头两个参数就可以准确地定位到盘体中的某个磁道，一个磁道上有 63 个扇区，我们只要再知道扇区的编号，就可以完成在三维空间中定位扇区的任务了， C/H/S 三个参数就是这样定位扇区的。

柱面编号从 0 开始，每个柱面有 255 个磁头，编号从 0 到 254 ，每磁道有 63 个扇区，编号从 1 到 63 。有朋友问：难道硬盘中真的有 255 个磁头吗？当然不是，硬盘中的磁头很少会超过 4 个，真正硬盘的每个磁道也不是都有 65 个扇区。每柱面 255 磁头每磁道 63 扇区这种模型只是为了研究问题方便而人为规定出来的，就象我们规定每小时有 60 分钟而每分钟有 60 秒那样。虽然柱面中的磁头数量和实际不符，但由于硬盘中有一个地址翻译器，可以将标准模型中的 CHS 参数转换为硬盘实际的 CHS 参数，因此我们用 C/H/S 定位扇区是没有问题的，这就象可以从阴历的日期转换为阳历的日期。

柱面是研究分区非常重要的一个参数，分区以柱面为粒度。这话怎么理解？操作系统分区时要考虑柱面因素，分区总是结束在柱面的最后一个扇区，也就是说分区总是结束在某个柱面的 254 磁头 63 扇区。这就解释了为什么你要求的分区大小和实际分区大小总是有些小小的误差，例如你要分一个区是 200M ，操作系统在分区时考虑的是这个分区到到哪个柱面结束离你的要求误差最小。 这种以柱面为粒度的分区方式肯定会有误差，误差不会超过半个柱面，一个柱面的大小是 255 磁头× 63 扇区× 512 字节＝ 7.8M

LBA 定位扇区的方式就简单多了， LBA 方法是把硬盘当作一个扇区集合， LBA 给硬盘中的每个扇区都赋予一个唯一的编号，只要你说出扇区编号就可以定位出扇区位置。 LBA 只用了一个参数，而 C/H/S 用了三个参数，两种方式可以相互转换。就象我们习惯用年月日来表示历史上的某一天，但其实也可以直接说今天是公元某某天。 硬盘上的第一个扇区用 C/H/S 表示是 0/0/1 ， 0 柱面 0 磁头 1 扇区，用 LBA 表示就是 0 号扇区。 C/H/S 和 LBA 之间有转换公式，但我很少会手工计算，我一般都利用 Winhex 帮忙，例如我想知道 950/254/63 对应的 LBA 是多少，我就在 Winhex 中选择转到扇区，如下图所示，输入 C/H/S 参数。

 

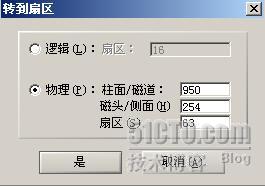
Winhex 转到指定扇区后会同时显示显示 C/H/S 和 LBA 参数，如下图所示， Winhex 告诉我们 950/254/63 对应的 LBA 参数是 15277814 。从 LBA 转换 C/H/S 也可用同样方法。

 

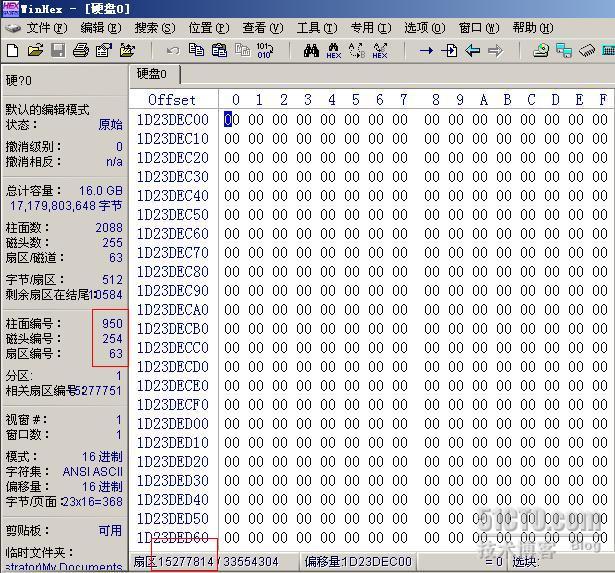
好了，掌握了这些基础知识，我们就可以来分析分区表了。分区表在硬盘的第一个扇区， 0 柱面 0 磁头 1 扇区，这个扇区也被称为 MBR ，主引导记录。 MBR 有 512 个字节，分为三部分内容，第一部分是个引导程序， 446 字节；第二部分是分区表， 64 字节；第三部分是结束标志，内容是 55AA ， 2 字节。如下图所示就是 MBR 的内容，绿色部分为分区表。

 

分区表有 64 个字节，可以表示 4 项分区，每项分区为 16 个字节。我们只要把 16 个字节的内容搞清楚了，分区表就不再神秘了。上图所使用的计算机硬盘分了四个区，如下图所示，是大家常用的分区方法，一个主分区，一个扩展分区，扩展分区内分了三个逻辑分区。

 

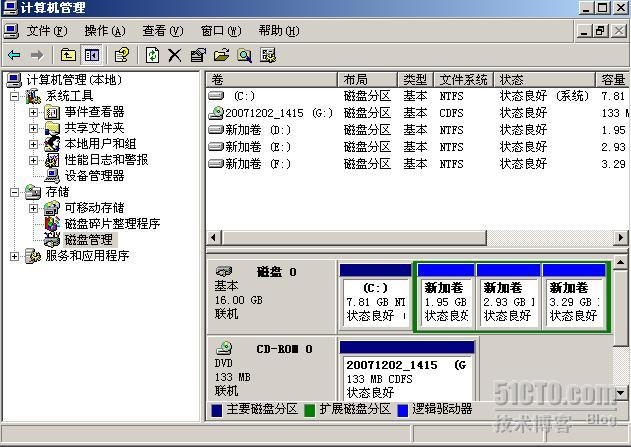
这四个分区在分区表中如何表现呢？我们从图中可以看出分区表中只有两项内容，分别是

80 01 01 00 07 FE FF FB 3F 00 00 00 BD 08 FA 00 ， 00 00 C1 FC 0F FE FF FF FC 08 FA 00 2C CD 05 01 。这意味着 MBR 的分区表中只定义了两个分区，我们一个一个来分析，先分析第一个分区表项， 80 01 01 00 07 FE FF FB 3F 00 00 00 BD 08 FA 00 ，我们先解释一下这 16 个字节的含义。

第一个字节的内容是分区的引导标志 ， 80 表示是引导分区， 00 表示不是引导分区。第二，三， 4 字节表示分区的起始磁头，扇区，柱面 ，本例中三个参数分别是 01 01 00 ，这代表第一个分区从 0 柱面 1 磁头 1 扇区开始。第五个字节表示分区类型 ， 07 表示 NTFS 分区，常用的类型有 0F （扩展分区）， 0B （ FAT32 ）， 06 （ FAT16 ）。第六，七，八字节分别表示分区的结束磁头，扇区，柱面 。注意，这里有些玄机，分区的起始扇区和结束扇区看起来用了一个完整字节，其实不是。由于 C/H/S 中扇区编号从 1 到 63 ，因此用一个字节表示有些浪费，一个字节由八个二进制数组成，扇区编号只用了低六位，高 2 位给柱面用了。因此，表示柱面其实用了 10 个二进制数，其中高 2 位是从扇区参数中借来的 。 结合本例看看，六，七，八参数分别是 FE FF FB ，分析一下， FE 表示分区的结束磁头是 254 ， FF 拆为二进制是 11111111 ，低六位是 111111 ，用来表示分区的结束扇区，也就是说结束扇区是 63 。 FF 拆开后高 2 位 11 给了柱面用，也就是说分区的结束柱面不是 FB ，而是 3FB ， 3FB 等于十进制的 1019 。这下子我们明白了，第一个分区开始在 0/1/1 ，结束在 1019/254/63 。

看到这里有些朋友不禁有些疑问，分区表只用了八个字节就已经表示了起始和结束位置，为什么还需要后八个字节呢？其实后八个字节是用 LBA 方法来表示分区的起始位置和结束位置，这可不是多此一举，主要是因为 CHS 对大容量硬盘已经力不从心了。从刚才的参数分析我们可以看出来， CHS 表示柱面的参数最多也就是 10 个二进制数， 10 个二进制数只能表示 1024 个柱面， 1024 柱面才多大？ 1024 × 7.8M ＝ 8G 。看看， C/H/S 无法定位 8G 以后的硬盘空间，这也是当初设计分区表时目光短浅，如果能用两个字节表示柱面，那现在就完全没问题了。由于 C/H/S 对现在的海量硬盘根本无用武之地，因此表示分区大小的重任就只能落在 LBA 的肩上了。

继续分析分区表项的第九，十，十一，十二字节，这四个字节代表分区之前的扇区数 ，意思是从分区的起始到硬盘的第一个扇区之前有多少扇区，其实是很隐晦地告诉我们分区从哪里起始。本例中这四个字节的内容是 3F 00 00 00 ，首先我们要高低位互换，四个字节的内容是 00 00 00 3F ，转为 10 进制是 63 ，这意味着第一个分区之前的扇区数是 63 ，也意味着第一个分区从 63 扇区开始。为什么？有人这么问，既然第一个分区之前有 63 个扇区，那第一个分区应该从 64 扇区开始才对呀？主要是因为 LBA 表示扇区是从 0 开始编号而不是从 1 开始，分区之前有 63 个扇区意味着分区之前的扇区是从 0 到 62 ，那分区起始自然应该从 63 开始。

分区表的十三，十四，十五，十六字节代表分区的大小 ，这四个字节表示分区的扇区数。本例这四个参数为 BD 08 FA 00 ，高低位互换一下，分区的扇区数为 00 FA 08 BD ，换算为 10 进制为 16386237 。知道了分区起始在 63 ，大小为 16386237 ，结束位置也就知道了 63+ 16386237 － 1 ＝ 16386299 。用 winhex 转到 16386299 看看，如下图所示， 16386299 正是 1019 柱面 254 磁头 63 扇区。

 

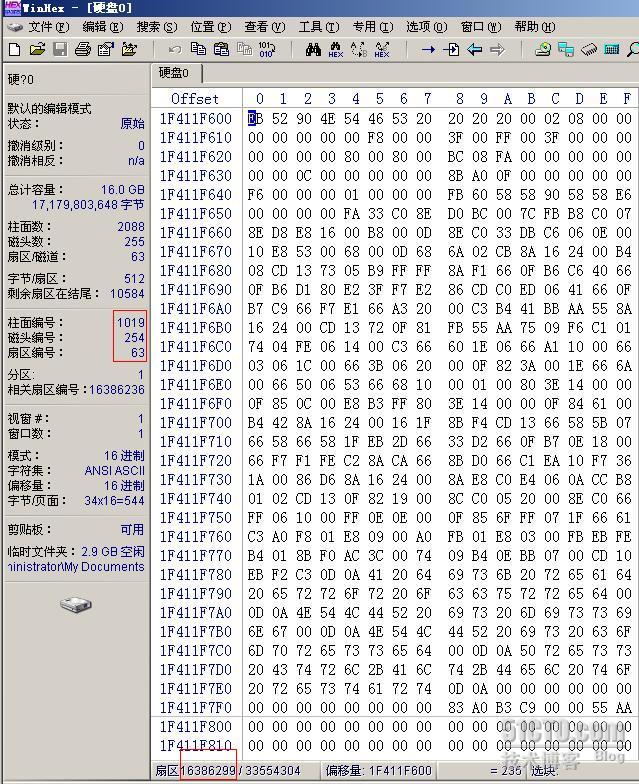
对分区表的第一个项内容总结一下，这 16 个参数告诉我们，第一个分区从 0/1/1 开始，到 1019/254/63 结束，可以引导系统，分区类型为 NTFS ，分区起始的扇区数是 63 ，分区大小是 16386237 扇区。以前有同学提过问题，分区为什么不从第二个扇区开始？主要是因为 MBR 太重要，操作系统不希望对此扇区进行太多访问，因此干脆把 MBR 所在的整个磁道都划到分区之外了， 这就是为什么第一个分区从 0 柱面 1 磁头 1 扇区开始。

分析了分区表的第一项，接下来来分析第二项 00 00 C1 FC 0F FE FF FF FC 08 FA 00 2C CD 05 01 。第二项前八个字节中我们只要看第一个字节和第五个字节，知道第二个分区是扩展分区，不能引导，这就够了。其余 6 个字节用 C/H/S 表示分区的起始和结束就不用再看了，因为 8G 以后 C/H/S 已经失去作用了，第二个扩展分区结束的位置远远超过 8G ， C/H/S 肯定无法表示了，主要看看后八个字节的 LBA 参数就可以了。扩展分区之前的扇区数是 FC 08 FA 00 ，高低位互换后是 00 FA 08 FC ，也就是扩展分区之前的扇区数是 16386300 ，扩展分区的起始是 16386300 扇区。扩展分区的大小是 2C CD 05 01 ，高低位互换后再转为 10 进制是 17157420 扇区，因此可算出分区的结束是在 16386300 ＋ 17157420-1=33543719 扇区。扩展分区的起点和终点都知道了，通过 Winhex 查询 C/H/S 参数，可知分区的起始是 1020/0/1 ，结束在 2087/254/63 。

 

分析了 MBR 的分区表后，我们发现分区表中定义了两个分区，一个是主分区，一个是扩展分区。看到这里，有人要问了，这个硬盘明明有四个分区，怎么在分区表中只定义了两项？到目前为止，只有 C 分区被定义出来， D ， E ， F 分区在哪里定义呢？答案在扩展分区里，在扩展分区的第一个扇区，有一个分区表，分区表中将定义出主分区 D ，然后定义出下一个扩展分区。找到下一个扩展分区的起始扇区，又会看到一个分区表，定义出主分区 E ，然后又定义下一个扩展分区 …… 这种依靠扩展分区的方法被称为链式分区表，其实使用扩展分区也是无奈之举，由于 MBR 的分区表只有 4 项， 我们如果不使用扩展分区就最多只能使用四个分区。有了扩展分区之后，显然分区的数量就不受限制了，而且现在从分区表的角度来看，分区表中只有主分区和扩展 分区，根本没有逻辑分区。我们使用的逻辑分区，不过是在扩展分区的分区表中定义出来的主分区而已。分区拓扑如下图所示。

 

我们转到扩展分区的起始，继续向下分析分区表，扩展分区的起始位置在 1020/0/1 ，分区表内容如下图所示

 

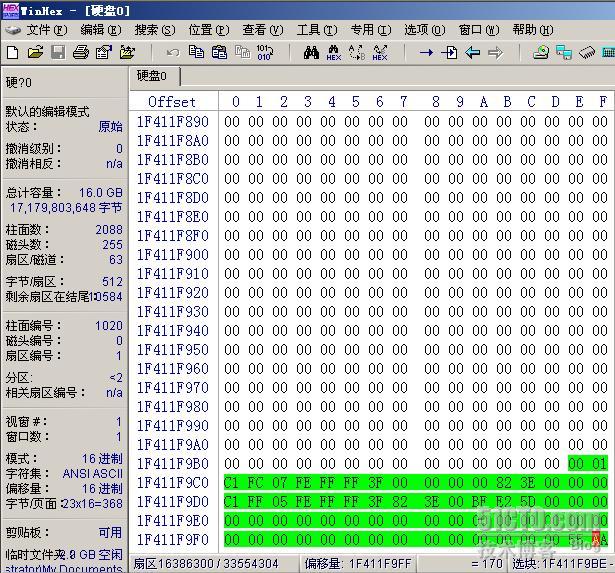
从扩展分区的分区表中可以看出定义了两项分区，分别来分析一下。第一项定义了 D 分区，内容是 00 01 C1 FC 07 FE FF FF 3F 00 00 00 82 3E 00 00 ，根据分区类型参数可以知道 D 分区是一个 NTFS 主分区，由于 D 分区的结束位置超过了 8G ，因此不用看 C/H/S 参数，直接看 LBA 就可以了。 3F 00 00 00 表示 D 分区之前的扇区是 63 ，注意，这可不代表 D 分区的起始位置是 63 。扩展分区表中描述主分区之前的扇区数基本都是 63 ，这个 63 指的是从 D 分区的起始到定义 D 分区的分区表之间的距离是 63 扇区，扩展分区的分区表在 16386300 扇区，因此 D 分区的起始应该是 16386300 ＋ 63 ＝ 16386363 ， C/H/S 参数是 1020/1/1 。 00 82 3E 00 表示分区的大小是 3E 82 00 扇区，经计算可知分区的结束位置在 20482874 ， C/H/S 参数是 1274/254/63 。

接下来分析第二项，这一项定义的是第二个扩展分区，内容是 00 00 C1 FF 05 FE FF FF 3F 82 3E 00 BF E2 5D 00 。分区类型 05 表示定义的是一个扩展分区， 00 3E 82 3F 表 示第二个扩展分区之前的扇区数，注意，之前的扇区数指的是从第二个扩展分区的起点到第一个扩展分区起点的距离，以后向下定义后续扩展分区时，之前的扇区数 指的都是被定义的扩展分区的起点到第一个扩展分区起点的距离。现在我们来计算一下第二个扩展分区的起始位置，第二个扩展分区距离第一个扩展分区的起点有 3E 82 3F 个扇区，第一个扩展等区的起点是 16386300 ，因此第二个扩展分区的起始是 16386300 ＋ 4096575 （ 3E823F ）＝ 20482875 ， C/H/S 参数是 1275/0/1 。第二个扩展分区的大小是 5D E2 BF ，所以我们推算出第二个扩展分区的终点是 26635769 ， C/H/S 是 1657/254/63 。

扩展分区的分区表分析完之后， D 分区被定义出来了，而且又给出了第二个扩展分区的定义，我们现在到第二个扩展分区的起点，继续向下分析分区表。第二个扩展分区的位置在 1275/0/1 ，分区表内容如下图所示。

 

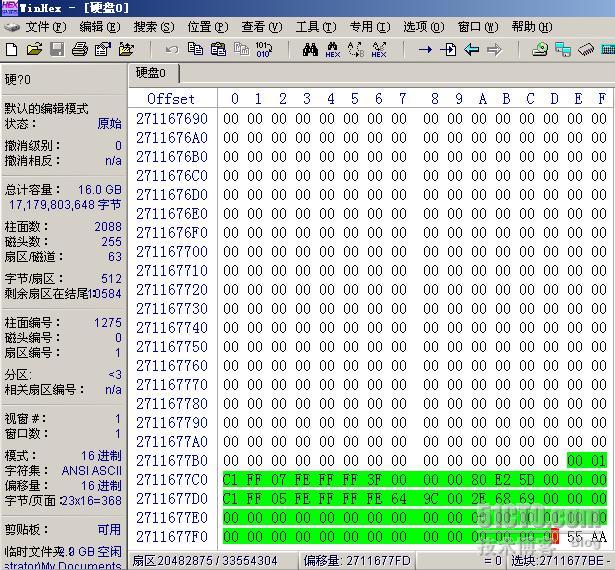
分区表中仍然是两项，这次我们明白了，肯定一项用来定义 E 分区，另一项定义第三个扩展分区。先来看看第一项 00 01 C1 FF 07 FE FF FF 3F 00 00 00 80 E2 5D 00 ，从分区类型 07 可以得知 E 的分区类型是 NTFS ， E 分区之前的扇区数是 00 00 00 3F ，这指的是 E 分区的起点和第二个扩展分区表之间的距离是 63 扇区。第二个扩展分区表在 20482875 ，所以 E 的起点应该是 20482875 ＋ 63 ＝ 20482938 。再根据 E 的大小是 00 5D E2 80 ，可以计算出 E 的终点是 26635769 。 E 从 20482938 － 26635769 ，用 C/H/S 表示是 1275/1/1 － 1657/254/63 。

再来看分区表的第二项，这一项将定义第三个扩展分区， 00 00 C1 FF 05 FE FF FF FE 64 9C 00 2E 68 69 00 。 05 表示定义的是扩展分区， 00 9C 64 FE 表示的是第三个扩展分区之前的扇区数，之前指的是到第一个扩展分区的起点，也就是说第三个扩展分区的起点和第一个扩展分区起点之间的距离是 10249470 （ 00 9C 64 FE ）个扇区。由于第一个扩展分区的起始是 16386300 ，因此第三个扩展分区的起始位置应该是 16386300 ＋ 10249470 ＝ 26635770 。第三个扩展分区的大小是 00 69 68 2E ，因此第三个扩展分区的终点应该是 26635770 ＋ 6907950 （ 00 69 68 2E ）－ 1 ＝ 33543719 。第三个扩展分区起点和终点是 26635770 － 33543719 ，用 C/H/S 表示是 1658/0/1 － 2087/254/63 。

 

第二个扩展分区的分区表分析完后， E 分区被定义出来，第三个扩展分区也被定义出来了。第三个扩展分区的起点在 1658/0/1 ，内容如下图所示。

 

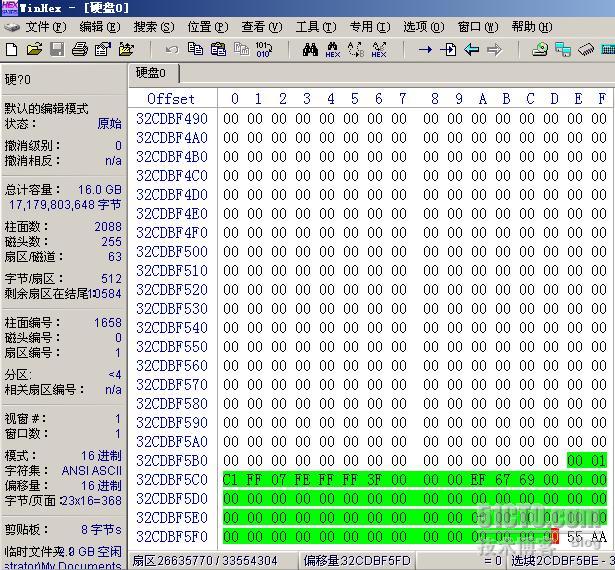
这次我们发现分区表中只有一项，这是因为已经定义到最后一个分区了，因此不需要再向下定义扩展分区了。最后一项分区定义了 F 分区，内容是 00 01 C1 FF 07 FE FF FF 3F 00 00 00 EF 67 69 00 ， 07 表示 F 分区是一个 NTFS 主分区， 00 00 00 3F 表示 F 分区和第三个扩展分区分区表的距离是 63 扇区，第三个扩展分区的起点是 26635770 ，所以 F 分区的起始位置是 26635770 ＋ 63 ＝ 26635833 。 F 分区的大小是 00 69 67 EF ，因此计算出 F 分区的终点是 33543719 。 F 分区的起点和终点是 26635833 － 33543719 ， 1658/1/1 － 2087/254/63 。

 

至 此，分区表分析完毕，一共分析了四处分区表，定义了七个分区，各处分区表定义的分区具体如下表。如果大家能够细细体会，察觉到操作系统分区的规律，将来进 行分区恢复就容易得多了。当我们明白操作系统创建分区和修改分区在分区表中是怎么表现的，将来进行分区恢复只不过是一个简单的逆向操作而已，下次我们可以 举个例子来说明一下。分区恢复并不难，大家只要渡过开始时对操作界面的不适应，仔细研究，辅以实例好好推敲一番，定然能够柳暗花明，豁然开朗。恭祝大家早 日掌握分区原理！

MBR	C ： 0/1/1 － 1019/254/63  63 － 16386299
	第一扩展分区 1020/0/1 － 2087/254/63  16386300 － 33543719
第一个扩展分区的分区表	D: 1020/1/1 － 1274/254/63  16386363 － 20482874
	第二个扩展分区 1275/0/1 － 1657/254/63  20482875 － 26635769
第二个扩展分区的分区表	E: 1275/1/1 － 1657/254/63  20482938 － 26635769
	第三个扩展分区 1658/0/1 － 2087/254/63  26635770 － 33543719
第三个扩展分区的分区表	F: 1658/1/1 － 2087/254/63  1658/1/1 － 2087/254/63

 

本文出自 “岳雷的微软网络课堂 ” 博客，转载请与作者联系！