求这100人一周课外阅读高中数学题

从某校随机抽取100名学生，获得了他们一周课外阅读时间(单位：小时)的数据，整理得到数据分组及频数分布表和频率分布直方图.

组号	分组	频数
1	[0,2)	6
2	[2,4)	8
3	[4,6)	17
4	[6,8)	22
5	[8,10)	25

续表

6	[10,12)	12
7	[12,14)	6
8	[14,16)	2
9	[16,18)	2
合计	100

 

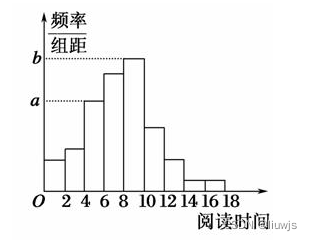
(1)从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；

(2)求频率分布直方图中的a，b的值；

(3)假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组．(只需写出结论)

答案：

解　(1)根据频数分布表，100名学生中课外阅读时间不少于12小时的学生共有6＋2＋2＝10名，所以样本中的学生课外阅读时间少于12小时的频率是1－＝0.9.

从该校随机选取一名学生，估计其课外阅读时间少于12小时的概率为0.9.

(2)课外阅读时间落在组[4,6)的有17人，频率为0.17, 所以a＝＝＝0.085.

课外阅读时间落在组[8,10)的有25人，频率为0.25，所以b＝＝＝0.125.

 

(3)样本中的100名学生课外阅读时间的平均数在第4组．