Online Learning算法理论与实践

背景

Online Learning是工业界比较常用的机器学习算法，在很多场景下都能有很好的效果。本文主要介绍Online Learning的基本原理和两种常用的Online Learning算法：FTRL（Follow The Regularized Leader）[1]和BPR（Bayesian Probit Regression）[2]，以及Online Learning在美团移动端推荐重排序的应用。

什么是Online Learning

准确地说，Online Learning并不是一种模型，而是一种模型的训练方法，Online Learning能够根据线上反馈数据，实时快速地进行模型调整，使得模型及时反映线上的变化，提高线上预测的准确率。Online Learning的流程包括：将模型的预测结果展现给用户，然后收集用户的反馈数据，再用来训练模型，形成闭环的系统。如下图所示：

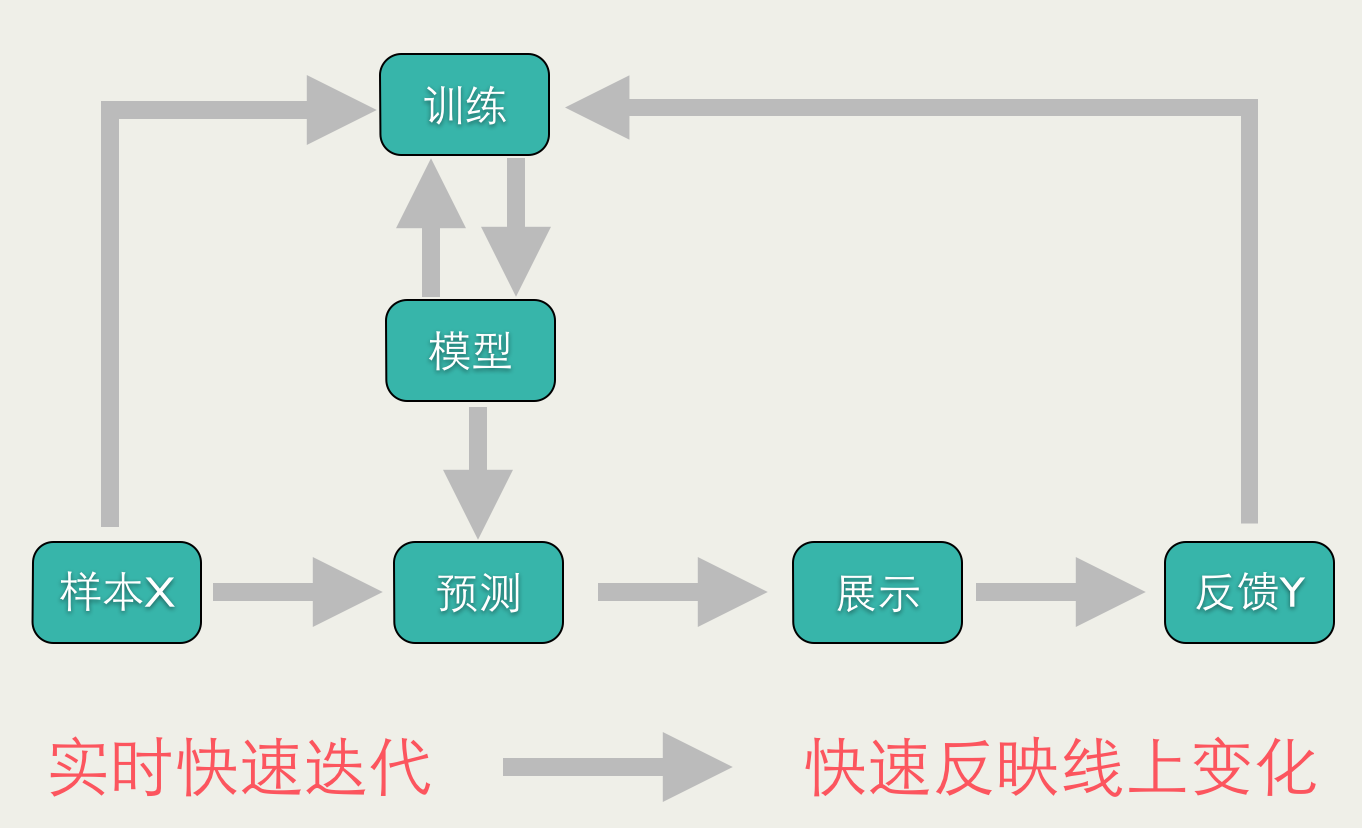
Online Learning有点像自动控制系统，但又不尽相同，二者的区别是：Online Learning的优化目标是整体的损失函数最小化，而自动控制系统要求最终结果与期望值的偏差最小。

传统的训练方法，模型上线后，更新的周期会比较长（一般是一天，效率高的时候为一小时），这种模型上线后，一般是静态的（一段时间内不会改变），不会与线上的状况有任何互动，假设预测错了，只能在下一次更新的时候完成更正。Online Learning训练方法不同，会根据线上预测的结果动态调整模型。如果模型预测错误，会及时做出修正。因此，Online Learning能够更加及时地反映线上变化。

Online Learning的优化目标

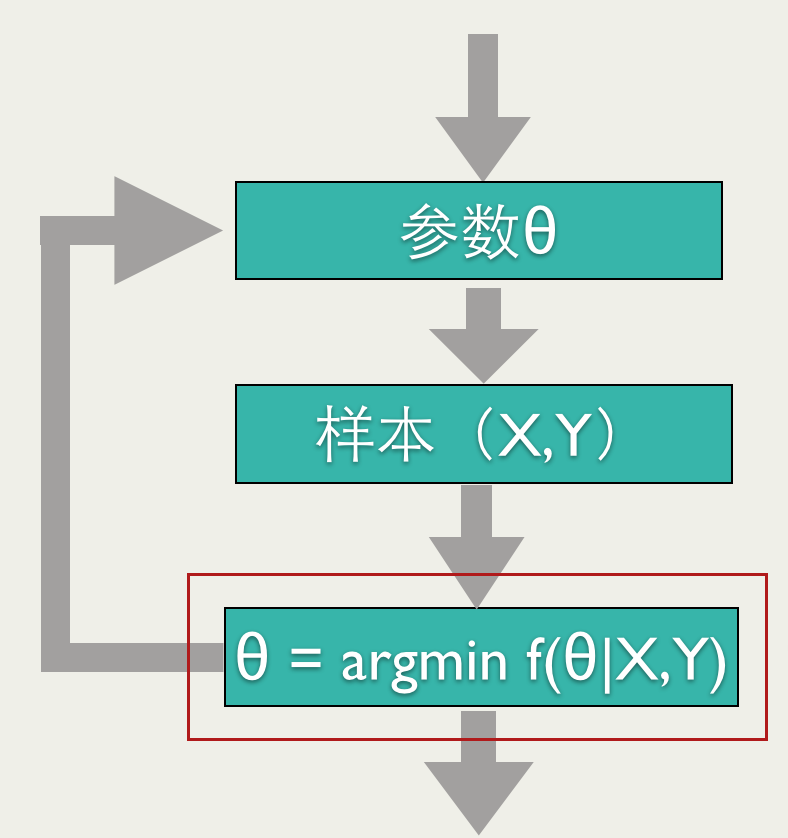
如上图所示，Online Learning训练过程也需要优化一个目标函数（红框标注的），但是和其他的训练方法不同，Online Learning要求快速求出目标函数的最优解，最好是能有解析解。

怎样实现Online Learning

前面说到Online Learning要求快速求出目标函数的最优解。要满足这个要求，一般的做法有两种：Bayesian Online Learning和Follow The Regularized Leader。下面就详细介绍这两种做法的思路。

Bayesian Online Learning

贝叶斯方法能够比较自然地导出Online Learning的训练方法：给定参数先验，根据反馈计算后验，将其作为下一次预测的先验，然后再根据反馈计算后验，如此进行下去，就是一个Online Learning的过程，如下图所示。

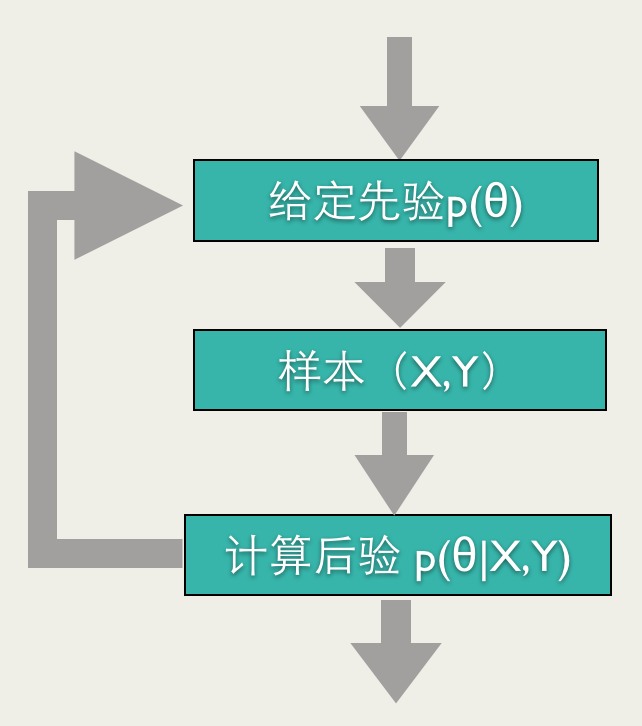
举个例子， 我们做一个抛硬币实验，估算硬币正面的概率\( \mu \)。我们假设\( \mu \)的先验满足 $$ p\left(\mu \right) = \operatorname{Beta}(\alpha, \beta)$$ 对于观测值\( Y＝1 \)，代表是正面，我们可以算的后验： $$p\left( \mu | Y=1 \right) = \operatorname{Beta}(\alpha+1, \beta)$$ 对于观测值\( Y＝0 \)，代表是反面，我们可以算的后验： $$ p\left(\mu \right | Y=0) = \operatorname{Beta}(\alpha, \beta+1)$$ 按照上面的Bayesian Online Learning流程，我们可以得到估算\( \mu \)的Online Learning算法： >初始化 \( \alpha \),\( \beta \) >for i = 0 … n >>如果 \( Y_i \)是正面 >> \( \alpha = \alpha + 1 \) >>如果 \(Y_i\)是反面 >>\( \beta = \beta + 1 \)   最终: \( \mu \sim \operatorname{Beta}(\alpha, \beta) \)，可以取\( \mu \)的期望，\( \mu = \frac{\alpha}{\alpha+\beta}\) 假设抛了\(N\)次硬币，正面出现\(H\)次，反面出现\(T\)次，按照上面的算法，可以算得： $$ \mu = \frac{ \alpha + H}{\alpha + \beta + N} $$ 和最大化似然函数： $$ \mathrm{log}\left[ p\left(\mu \mid \alpha,\beta \right) \cdot p \left( Y = 1 \mid \mu \right)^{H} \cdot p \left( Y = 0 \mid \mu \right)^{T} \right] $$ 得到的解是一样的。

上面的例子是针对离散分布的，我们可以再看一个连续分布的例子。

有一种测量仪器，测量的方差\( \sigma^2\)是已知的， 测量结果为：\( Y_1 ,