深度强化学习实践 Maxim Lapan 章节8：DQN的扩展

最新推荐文章于 2025-12-22 20:07:09 发布

原创最新推荐文章于 2025-12-22 20:07:09 发布 · 662 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #人工智能 #回归 #强化学习

深度强化学习专栏收录该内容

22 篇文章

订阅专栏

我个人觉得这一章节是重中之重的，所以这里我要自己写个Notice,这一章节，我们将会学习到绝大部分DQN上的优化的内容，我觉得这一章学完就算是真正的入门了DQN了，可以开始做自己想学习的事情.

对了，我要在这里说明一下，我这边完全只是读了书分享一下，有些书里面的我觉得最重要的部分和一些我遇到的坑，大家想学真东西的还是要自己去看书，书也不贵，也就100不到。这只是一个讨论Blog哈，更多的只是为了自己的有个记录，确定的输出这样子。

重要ing

基础DQN

就是我们之前的DQN，但是这里做了PTAN的封装，这里使用了一种新的方式，所所以这里是封装了基本上所有的超参的内容，然后把剩下的部分直接放到了

    'pong': SimpleNamespace(**{
        'env_name':         "PongNoFrameskip-v4",
        'stop_reward':      18.0,
        'run_name':         'pong',
        'replay_size':      100000,
        'replay_initial':   10000,
        'target_net_sync':  1000,
        'epsilon_frames':   10**5,
        'epsilon_start':    1.0,
        'epsilon_final':    0.02,
        'learning_rate':    0.0001,
        'gamma':            0.99,
        'batch_size':       64
    }),

坑

每章必坑，这个已经升级到了gymnasium，但是貌似之前的ptan只是支持到了gym，stable_baselines的AtariWrapper的WarpFrame需要检查我们的assert isinstance(env.observation_space, spaces.Box), f"Expected Box space, got {env.observation_space}"，但是传入的是gym的obs也就是BOX(210,160,3),这个是不满足条件的，所以我这边想了一些其他的方法，但是支持的程度不好，所以直接注释了，我看了实现是可以转成需要的84841的input的

unpack_batch

这个函数最主要的输出就是几点，第一个是一个@no_grad的函数，表示这里面的所有的操作不会记录到计算图里面，通过last_state来判断是不是done了，如果done，则last_state使用state来代替），使用了done_mask来选择对应的

dqn_basic

注意用到了，gamma的参数，使用了firstlast的buffer经验回放池

#!/usr/bin/env python3
import gym
import ptan
import argparse
import random

import torch
import torch.optim as optim

from ignite.engine import Engine

from lib import dqn_model, common

NAME = "01_baseline"


if __name__ == "__main__":

	# 初始化内容,最终创建一个replaybuffer和一个optimizer
    random.seed(common.SEED)
    torch.manual_seed(common.SEED)
    params = common.HYPERPARAMS['pong']
    parser = argparse.ArgumentParser()
    parser.add_argument("--cuda", default=False, action="store_true", help="Enable cuda")
    args = parser.parse_args()
    device = torch.device("cuda" if args.cuda else "cpu")

    env = gym.make(params.env_name)
    env = ptan.common.wrappers.wrap_dqn(env)
    env.seed(common.SEED)

    net = dqn_model.DQN(env.observation_space.shape,
                        env.action_space.n).to(device)

    tgt_net = ptan.agent.TargetNet(net)
    selector = ptan.actions.EpsilonGreedyActionSelector(
        epsilon=params.epsilon_start)
    epsilon_tracker = common.EpsilonTracker(selector, params)
    agent = ptan.agent.DQNAgent(net, selector, device=device)

    exp_source = ptan.experience.ExperienceSourceFirstLast(
        env, agent, gamma=params.gamma)
    buffer = ptan.experience.ExperienceReplayBuffer(
        exp_source, buffer_size=params.replay_size)
    optimizer = optim.Adam(net.parameters(),
                           lr=params.learning_rate)
	# 定义我们的批处理操作，
    def process_batch(engine, batch):
        optimizer.zero_grad()
        loss_v = common.calc_loss_dqn(
            batch, net, tgt_net.target_model,
            gamma=params.gamma, device=device)
        loss_v.backward()
        optimizer.step()
        epsilon_tracker.frame(engine.state.iteration)
        if engine.state.iteration % params.target_net_sync == 0:
            tgt_net.sync()
        return {
            "loss": loss_v.item(),
            "epsilon": selector.epsilon,
        }

    engine = Engine(process_batch)
    common.setup_ignite(engine, params, exp_source, NAME)
    engine.run(common.batch_generator(buffer, params.replay_initial,
                                      params.batch_size))

跑起来的训练的结果可以看到，大概一个小时的时间可以从-21训练到16左右的水平，虽然不是很稳定，但是还是可以看到明显在训练，这个比我同样的环境，之前使用训练的结果要快很多，看来是对封装了很多内容。而且他可以把CPU和GPU跑满，我之前的GPU的利用率一直不太高，所以还是有效果的，可以尝试用用。

no_grad可以大大的加速训练，主要看你的
在这里插入图片描述
损失函数的需要注意，这里获取了新的批量设备，放到device(gpu),通过action和q_v获取到了对应的action的Q值，然后计算了bellman的目标网络值，注意中间使用到的no_grad的操作
next_state_vals[done_mask] = 0.0 是为了done的序列，直接配置next的价值为0


def calc_loss_dqn(batch, net, tgt_net, gamma, device="cpu"):
    states, actions, rewards, dones, next_states = \
        unpack_batch(batch)

    states_v = torch.tensor(states).to(device)
    next_states_v = torch.tensor(next_states).to(device)
    actions_v = torch.tensor(actions).to(device)
    rewards_v = torch.tensor(rewards).to(device)
    done_mask = torch.BoolTensor(dones).to(device)

    actions_v = actions_v.unsqueeze(-1)
    state_action_vals = net(states_v).gather(1, actions_v)
    state_action_vals = state_action_vals.squeeze(-1)
    with torch.no_grad():
        next_state_vals = tgt_net(next_states_v).max(1)[0]
        next_state_vals[done_mask] = 0.0

    bellman_vals = next_state_vals.detach() * gamma + rewards_v
    return nn.MSELoss()(state_action_vals, bellman_vals)

epsilon的decay的函数,通过我们的frame来计算当前合适的epsilon的值，batch_generate也很简单，直接使用了populate的函数，然后直接采样batch_size并且直接返回了


class EpsilonTracker:
    def __init__(self, selector: ptan.actions.EpsilonGreedyActionSelector,
                 params: SimpleNamespace):
        self.selector = selector
        self.params = params
        self.frame(0)

    def frame(self, frame_idx: int):
        eps = self.params.epsilon_start - \
              frame_idx / self.params.epsilon_frames
        self.selector.epsilon = max(self.params.epsilon_final, eps)




def batch_generator(buffer: ptan.experience.ExperienceReplayBuffer,
                    initial: int, batch_size: int):
    buffer.populate(initial)
    while True:
        buffer.populate(1)
        yield buffer.sample(batch_size)

setup_ignite

为什么这个函数单独开了一个小节，因为我之前用的也很少，这里可以详细的一起介绍一下加深一下印象，干脆单独开一个blog吧，后续写完了贴链接到这里

n步DQN

看过我们前面的blog的同学们应该已经非常的熟悉了，基于蒙特卡洛和TD(0)之间的n步DQN和之前的n步sarsa应该没有区别，具体的奖励函数这里我也不会放了，想看公式的可以参考专栏前面的文章。
考虑到具体的实现来说，

创建经验区的实际，需要指定gamma和step_count，这些都存放在了command的arg里面，原文中的最好的步骤大概是2-3步


    exp_source = ptan.experience.ExperienceSourceFirstLast(
        env, agent, gamma=params.gamma, steps_count=args.n)
        
    #以及计算损失函数的方式需要传入gamma
   loss_v = common.calc_loss_dqn(
            batch, net, tgt_net.target_model,
            gamma=params.gamma**args.n, device=device)
        loss_v.backward()

结果

兄弟们，怎么说呢，效果立竿见影。。。。。直接减少了1/2的时间。好用，爱用，以后常用

Episode 121: reward=18, steps=1850, speed=123.2 f/s, elapsed=0:30:47
Episode 122: reward=18, steps=1973, speed=123.2 f/s, elapsed=0:31:03
Episode 123: reward=18, steps=1957, speed=123.2 f/s, elapsed=0:31:19
Episode 124: reward=17, steps=2081, speed=123.2 f/s, elapsed=0:31:36
Episode 125: reward=14, steps=2101, speed=123.1 f/s, elapsed=0:31:54
Episode 126: reward=19, steps=1847, speed=123.1 f/s, elapsed=0:32:09

Double DQN

双Q网络，之前的Q值存在的高估的问题会导致陷入局部最优解，导致一直在选择一些前期收到了正反馈的动作的持续。
DDQN的想法就是随机使用一个Q值网络来进行动作选择，另一个Q值网络来进行Q值的计算，那么就可以解决高估的问题。但是我们现在已经有了一个目标网络了，所以这里的实现很简单，直接使用训练网络选择动作，但是目标网络来计算Q值，所以一开始计算损失函数的地方的Q值，可以很清晰的看到，对比直接使用tgt_net来计算Q值，我们这里重新使用了一个net来进行动作的推理以后的动作的Q值
损失函数对比
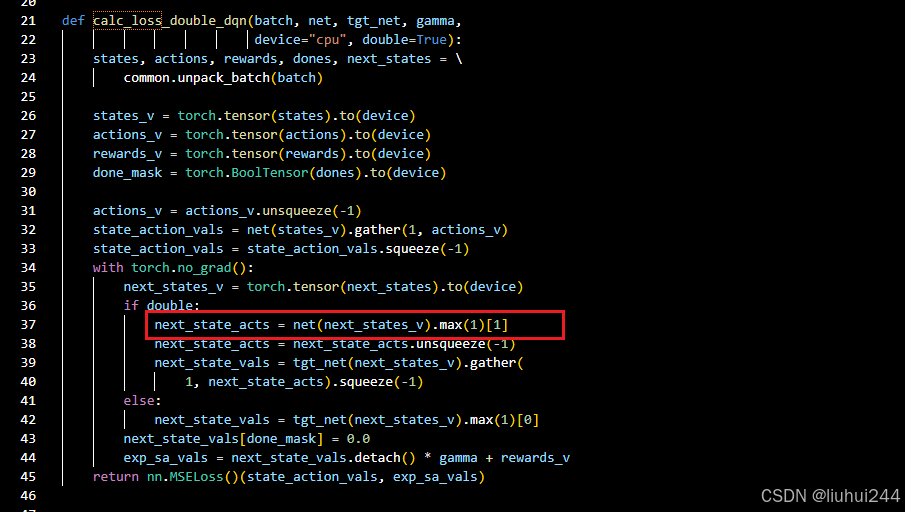
在这里插入图片描述

结果

实际的结果很一般哈，就是提升不明显，我这里就不详细的测试了，感兴趣的同学可以自己跑一下代码什么的，帮大家验证过了，效果一般。。。

噪声网络

这个是之前没有了解过的方法，先等等

优先级缓冲网络

之前已经讲解过了优先级缓冲网络的实现的方法，通过配置一些优先级来优先回放那些居然具有更高的优先级的经验回放案例，比如真的能得分的那些时刻，而不是平常的那些简单的时刻，我们之前的优先级的方法是通过delta来实现的，当和我们的期望的预期差异越大，则越应该快速更新

优先级网络的重要参数，一个是alpha，表示对于优先级的重视的程度，

每一个概率等于使用优先级的alpha次方来看待，probs = prios ** self.prob_alpha，接下来所有的概率都按照sum来相除得到一个归一化的概率分布，接下来就通过choice采样，同时返回的还有本次采样的权重，如果之前大家有印象的话，这里叫做重要度采样,是用来保证学习的正确性的，这里 $β\beta$ 也会慢慢的补偿到1，做到完全补偿
weights = (total * probs[indices]) ** (-self.beta)


    def sample(self, batch_size):
        if len(self.buffer) == self.capacity:
            prios = self.priorities
        else:
            prios = self.priorities[:self.pos]
        probs = prios ** self.prob_alpha

        probs /= probs.sum()
        indices = np.random.choice(len(self.buffer),
                                   batch_size, p=probs)
        samples = [self.buffer[idx] for idx in indices]
        total = len(self.buffer)
        weights = (total * probs[indices]) ** (-self.beta)
        weights /= weights.max()
        return samples, indices, \
               np.array(weights, dtype=np.float32)

新加入的样本会直接配置为max_prio，从而使得尽可能的优先采样我们的最新的样本（类似于在线）

优先级

看完了采样的时候是如何使用优先级的，这里看看如何进行初始化和popultae，主要修改的是新populate的时候优先级是当前的最大
self.priorities[self.pos] = max_prio


class PrioReplayBuffer:
    def __init__(self, exp_source, buf_size, prob_alpha=0.6):
        self.exp_source_iter = iter(exp_source)
        self.prob_alpha = prob_alpha
        self.capacity = buf_size
        self.pos = 0
        self.buffer = []
        self.priorities = np.zeros(
            (buf_size, ), dtype=np.float32)
        self.beta = BETA_START

    def update_beta(self, idx):
        v = BETA_START + idx * (1.0 - BETA_START) / \
            BETA_FRAMES
        self.beta = min(1.0, v)
        return self.beta

    def __len__(self):
        return len(self.buffer)

    def populate(self, count):
        max_prio = self.priorities.max() if \
            self.buffer else 1.0
        for _ in range(count):
            sample = next(self.exp_source_iter)
            if len(self.buffer) < self.capacity:
                self.buffer.append(sample)
            else:
                self.buffer[self.pos] = sample
            self.priorities[self.pos] = max_prio
            self.pos = (self.pos + 1) % self.capacity

更新优先级，如同我们前面所说，我们需要知道一个样本的delta值，知道我们的损失的具体的值，从而来配置不同的优先级的等级

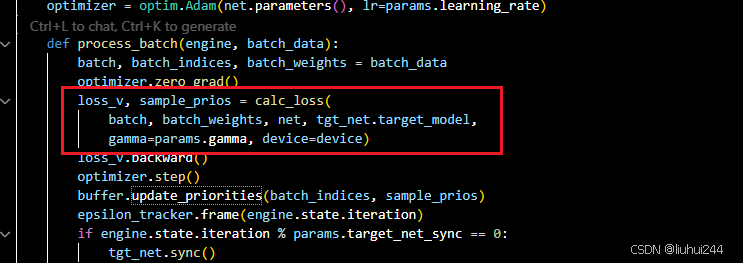
在这里插入图片描述

损失函数

手动实现了MSE的实现，保留了每一个sample的优先级，优先级直接等于losses_v，将会用于更新当前的sample的优先级的权重，注意会调用update函数用于更新beta值


def calc_loss(batch, batch_weights, net, tgt_net,
              gamma, device="cpu"):
    states, actions, rewards, dones, next_states = \
        common.unpack_batch(batch)

    states_v = torch.tensor(states).to(device)
    actions_v = torch.tensor(actions).to(device)
    rewards_v = torch.tensor(rewards).to(device)
    done_mask = torch.BoolTensor(dones).to(device)
    batch_weights_v = torch.tensor(batch_weights).to(device)

    actions_v = actions_v.unsqueeze(-1)
    state_action_vals = net(states_v).gather(1, actions_v)
    state_action_vals = state_action_vals.squeeze(-1)
    with torch.no_grad():
        next_states_v = torch.tensor(next_states).to(device)
        next_s_vals = tgt_net(next_states_v).max(1)[0]
        next_s_vals[done_mask] = 0.0
        exp_sa_vals = next_s_vals.detach() * gamma + rewards_v
    l = (state_action_vals - exp_sa_vals) ** 2
    losses_v = batch_weights_v * l
    return losses_v.mean(), \
           (losses_v + 1e-5).data.cpu().numpy()

结果

我这边还是跑了接近一个小时的时间才能收敛到19

Episode 159: reward=19, steps=1849, speed=96.5 f/s, elapsed=0:58:46
Episode 160: reward=17, steps=2371, speed=96.5 f/s, elapsed=0:59:11
Episode 161: reward=20, steps=2025, speed=96.5 f/s, elapsed=0:59:31
Episode 162: reward=18, steps=1829, speed=96.5 f/s, elapsed=0:59:50
Episode 163: reward=18, steps=2150, speed=96.5 f/s, elapsed=1:00:12
Episode 164: reward=19, steps=1861, speed=96.6 f/s, elapsed=1:00:31
Episode 165: reward=17, steps=2186, speed=96.6 f/s, elapsed=1:00:53
Episode 166: reward=18, steps=1950, speed=96.6 f/s, elapsed=1:01:13
Episode 167: reward=20, steps=1797, speed=96.7 f/s, elapsed=1:01:32
Episode 168: reward=19, steps=1798, speed=96.7 f/s, elapsed=1:01:50
Episode 169: reward=16, steps=2367, speed=96.7 f/s, elapsed=1:02:15
Episode 170: reward=17, steps=2236, speed=96.6 f/s, elapsed=1:02:38
Episode 171: reward=19, steps=2000, speed=96.7 f/s, elapsed=1:02:58
Episode 172: reward=18, steps=1756, speed=96.7 f/s, elapsed=1:03:17

原文中的线段最大的改变是损失值函数的下降，特别快的超越原本的basic的函数。

优化

现在的缓冲区的采样过于随意了，我觉得还是利用一些堆或者其他的一些数据结构什么的来加快回放缓冲区的优先级，也可以通过多次访问逐渐降低优先级的方式来实现，这样可以减少计算优先级的时间和复杂度，目前是O（N) ,如果是10000000的规模，我很难想象这个会对程序的速度的影响

原文的优化可以变成线段树，可能变成logN

dueling DQN

我们将Q值拆分成了V(s)和A(S,a)，表示的是状态S的价值和某个动作的动作优势的价值，显示的分开可以获得更好的稳定性和更快的收敛速度（减少互相反向干扰），但是其实我好奇如何在学习的过程中展现出这个差异性的，所以这里的将会生成两个网络的值（可能会共享一部分网络参数），
注意：任何状态的优势值之和是0 ：巧妙地的方法就是减去动作的平均值，这个显然可以保证优势网络的之和为0，显然我们这里需要做的最大的改动就是修改网络的结构

代码实现

核心差异就在于dqn的网络的差异，通过分离了两个网络出来，从而学习到了不同的v和a值的函数
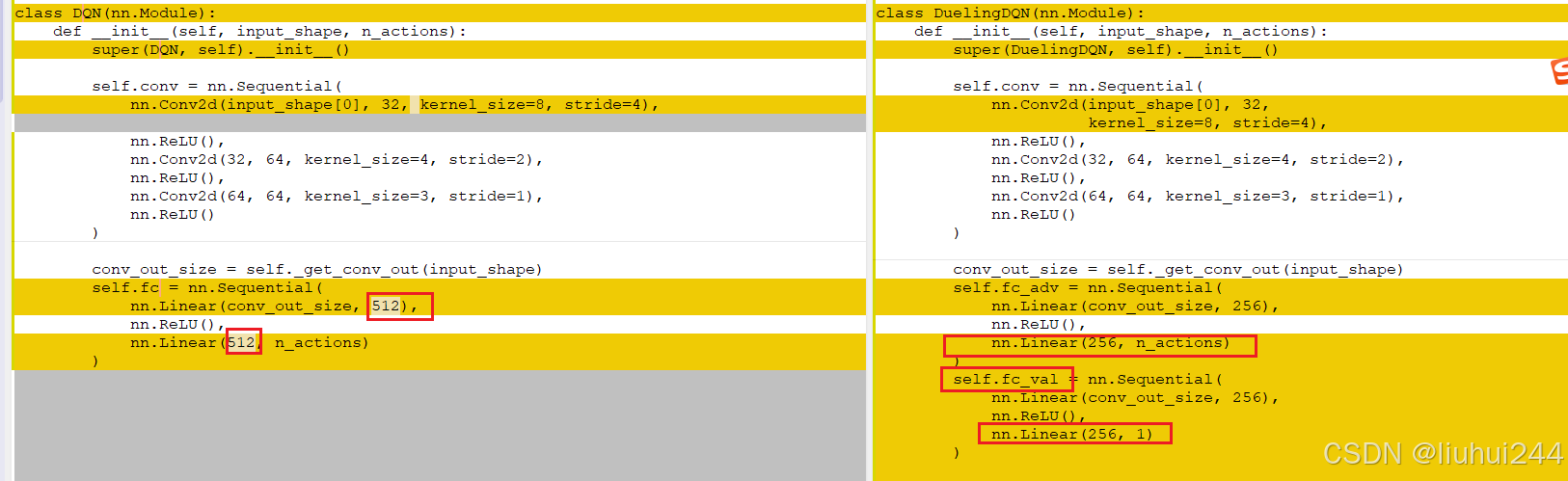
在这里插入图片描述
前向传播的在于这个点，注意val是一个(batch,1)的值 -mean就是我们需要的差值函数的均值

    def forward(self, x):
        adv, val = self.adv_val(x)
        return val + (adv - adv.mean(dim=1, keepdim=True))

    def adv_val(self, x):
        fx = x.float() / 256
        conv_out = self.conv(fx).view(fx.size()[0], -1)
        return self.fc_adv(conv_out), self.fc_val(conv_out)

结果

收敛时间1小时左右


Episode 152: reward=19, steps=1785, speed=103.1 f/s, elapsed=0:50:16
Episode 153: reward=17, steps=1925, speed=102.9 f/s, elapsed=0:50:37
Episode 154: reward=17, steps=2154, speed=102.6 f/s, elapsed=0:51:01
Episode 155: reward=17, steps=1935, speed=102.4 f/s, elapsed=0:51:22
Episode 156: reward=19, steps=1893, speed=102.2 f/s, elapsed=0:51:43
Episode 157: reward=16, steps=2118, speed=102.0 f/s, elapsed=0:52:06
Episode 158: reward=12, steps=2464, speed=101.8 f/s, elapsed=0:52:33
Episode 159: reward=20, steps=1794, speed=101.6 f/s, elapsed=0:52:53

RainBow

使用了n步的带优先级的带有高斯噪声的dueling网络的方法，就是我们的彩虹方法，一次性将所有不冲突的优化全部加入，高斯噪声的网络的论文会读一遍，到时候再来详细的介绍一下这里面的东西

结果

不得不说，真的好用，，但是16分钟搞定优化，而且直接学习到了21分的稳定状态，我觉得是相当的牛皮的。

Episode 51: reward=19, steps=1781, speed=91.0 f/s, elapsed=0:11:52
Episode 52: reward=21, steps=1530, speed=90.6 f/s, elapsed=0:12:13
Episode 53: reward=21, steps=1530, speed=90.1 f/s, elapsed=0:12:35
Episode 54: reward=14, steps=2470, speed=89.7 f/s, elapsed=0:13:11
Episode 55: reward=21, steps=1530, speed=89.5 f/s, elapsed=0:13:30
Episode 56: reward=21, steps=1530, speed=89.2 f/s, elapsed=0:13:51
Episode 57: reward=21, steps=1530, speed=88.8 f/s, elapsed=0:14:13
Episode 58: reward=21, steps=1530, speed=88.4 f/s, elapsed=0:14:36
Episode 59: reward=21, steps=1530, speed=88.0 f/s, elapsed=0:14:58
Episode 60: reward=21, steps=1530, speed=87.6 f/s, elapsed=0:15:20
Episode 61: reward=21, steps=1530, speed=87.2 f/s, elapsed=0:15:43
Episode 62: reward=21, steps=1530, speed=86.8 f/s, elapsed=0:16:05
Episode 63: reward=21, steps=1530, speed=86.4 f/s, elapsed=0:16:28
Episode 64: reward=21, steps=1530, speed=86.1 f/s, elapsed=0:16:51