Pytorch深度学习指南卷I --编程基础（A Beginner‘s Guide）第3章：一个简单的分类-优快云博客

本文链接：https://blog.youkuaiyun.com/liuhui244/article/details/145492785

过年回家浪了半个月，继续写我们的blog文件，完成我们的第三章的一个正式的分类的问题的代码的编写，原文中用了很多前面两张没有好好用过的方法，所以这里我们也会尽可能的将其介绍一下，便于后续的我们的很多的写法

数据准备

make_moon我们就会用来生成我们的测试数据

import numpy as np

#用于生成模型，优化器，函数，数据加载器
import torch
import torch.optim as optim
import torch.nn as nn
import torch.functional as F
from torch.utils.data import DataLoader, TensorDataset

from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, roc_curve, precision_recall_curve, auc

from stepbystep.v0 import StepByStep

分类问题

分类问题最简单的就是2元分类，

X, y = make_moons(n_samples=100, noise=0.3, random_state=0)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=.2, random_state=13)

#标准化数据
sc = StandardScaler()
sc.fit(X_train)

X_train = sc.transform(X_train)
X_val = sc.transform(X_val)

make_moon，train_test_split详解

用于生成半月形的数据，其中参数的含义如下

from sklearn.datasets import make_moons
make_moons(
    n_samples=100,      # 样本数量
    noise=0.0,         # 噪声水平
    random_state=None, # 随机种子
    shuffle=True      # 是否打乱数据
)

from sklearn.model_selection import train_test_split
# 基本语法
X_train, X_test, y_train, y_test = train_test_split(
    X,                  # 特征数据
    y,                  # 标签数据
    test_size=0.25,     # 测试集比例
    random_state=None,  # 随机种子
    shuffle=True,       # 是否打乱
    stratify=None       # 是否分层采样
)

可视化结果

这个是我这边的结果
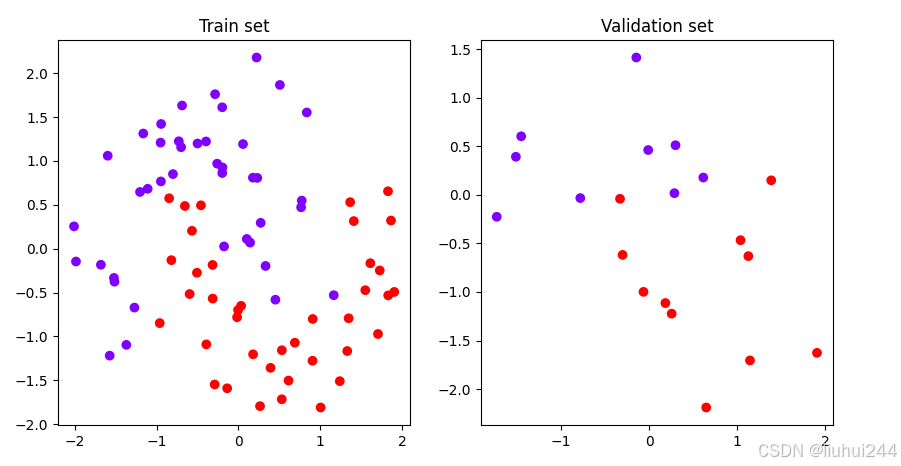
在这里插入图片描述

数据准备

#常见的数据准备，生成tensor的向量，发送到设备(使用时发送），生成dateset，生成dataloader
# Builds tensors from numpy arrays
x_train_tensor = torch.as_tensor(X_train).float()
y_train_tensor = torch.as_tensor(y_train.reshape(-1, 1)).float()

x_val_tensor = torch.as_tensor(X_val).float()
y_val_tensor = torch.as_tensor(y_val.reshape(-1, 1)).float()

# Builds dataset containing ALL data points
train_dataset = TensorDataset(x_train_tensor, y_train_tensor)
val_dataset = TensorDataset(x_val_tensor, y_val_tensor)

# Builds a loader of each set
train_loader = DataLoader(dataset=train_dataset, batch_size=16, shuffle=True)
val_loader = DataLoader(dataset=val_dataset, batch_size=16)

分类模型

logit回归

$logit(z) = b + w_1 x_1 + w_2x_2$ ，注意这里没有误差项（对比线性回归），因为我们将会将其发送到概率函数，我们最终会将其转变成一个是否为1的概率的值，值越大表示越可能为1.

比值比的概念：可以简单的理解为赔率，不同的事情发生和不发生的概率不一样，那么显然他们的权重也是不同的

def odds_ratio(prob):
    return prob / (1 - prob)

注意到我们想要的是大于0的时候，我们认为是正的概率更大，负的时候表示负的概念更大（也就是分类成另一种结果），所以我们使用了对数函数来实现了我们的值的转换，这就是我们之前说的核心的区别，当然我们需要的是一个对称的模型（不然如果不是对称的，例如正的范围更大，那么自然哪个是正标签哪个就更有可能被选中，这不是我们需要的结果）

def log_odds_ratio(prob):
    return np.log(odds_ratio(prob))

这里增加了了一个log，直观的图上的差异是，如下是odds的图像和经过了log转换后的图像

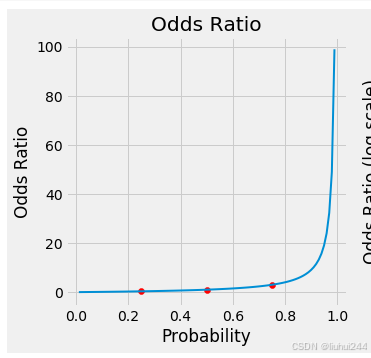
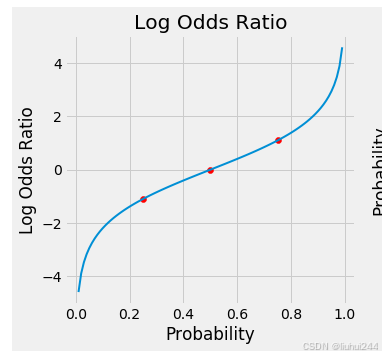
在这里插入图片描述

反转了log odds ratio和probability 就得到了我们的概率的函数，

$logoddsratio=log(p/(1−p))可得p=11+e−zlog_odds_ratio = log(p/(1-p)) 可得 p = \frac{1}{1+ e^{-z}}$ ，也就是我们的sigmoid函数，z是我们前面定义的logit函数（也就是线性函数的结果）

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

根据这个转换关系，p = sigmoid(z) 那么logit_odds = log_odd_ratio§ = p /(1-p)

非线性，激活函数

这里就不过多介绍了，因为我们之前的模拟都是线性的，显然无法满足很多不是非线性的情况，我们通过一些激活函数和中间的非线性层来经过一层非线性的转换。
在torch里面的表示就是

model1 = nn.Sequential()
model1.add_module('linear',nn.Linear(2,1))
model1.add_module('sigmoid',nn.Sigmoid())

注意Sigmoid函数没有需要学习的参数

损失函数

二元分类的损失函数是BCE（二元交叉熵）,BCE 损失函数需要由sigmoid函数返回的预测概率和真实标签y来计算，注意使用的是概率和真实标签（0 or 1）的差值来结算，，如果y是1的时候，就是偏离了1的的距离，如果是0的时候，那么就是偏离了0的距离，得到我们的公式如下
$BCE = - [y * l o g (p) + (1 - y) * l o g (1 - p)]$ ，注意如果1的标签的被认为是概率为0是1，那么损失函数将会无穷大，如果是有很多点，那么我们的损失误差就是误差值的平均值

#当然你可以直接使用nn自带的BCE损失函数
loss_fn = nn.BCELoss(reduction='mean')
dummy_labels = torch.tensor([1.0, 0.0])
dummy_predictions = torch.tensor([.9, .2])

# RIGHT
right_loss = loss_fn(dummy_predictions, dummy_labels)
# WRONG
wrong_loss = loss_fn(dummy_labels, dummy_predictions)

print(right_loss, wrong_loss)

尤其注意，这里的顺序很重要，因为通常使用的是预测在左，标签在右

BCEWithLogitsLoss

显然，我们刚刚使用的是概率标签，也就是经过了sigmoid函数处理后的结果的损失函数，如果我们使用这个损失函数，那么我们就只需要输出一个z的结果即可，换句话说，你不需要再来一层sigmoid层,我们之前使用的应该是mean模式

criterion = nn.BCEWithLogitsLoss(
    weight=None,              # 各样本权重
    reduction='mean',         # 降维方式：'none', 'mean', 'sum'
    pos_weight=None          # 正样本权重
)

所以这里我们就不再使用sigmoid函数，而是直接使用log_odds_ratio

logit1 = log_odds_ratio(.9)
logit2 = log_odds_ratio(.2)

dummy_labels = torch.tensor([1.0, 0.0])
dummy_logits = torch.tensor([logit1, logit2])

print(dummy_logits)


## 考虑到我们之前学习过的采样比，如果我们的数据不均衡可以增加一个positive的权重值，这样可以
# 但是需要注意的是，这里会导致我们的采样统计也会加权，这不是我们想要的，我们可以使用sum模式，然后手动的计算N，然后相除

开工，开工

准备好了这些东西，我们开始编写我们的模型

# Sets learning rate - this is "eta" ~ the "n" like Greek letter
lr = 0.1

#torch.manual_seed(42)
model = nn.Sequential()
model.add_module('linear', nn.Linear(2, 1))

# Defines a SGD optimizer to update the parameters
optimizer = optim.SGD(model.parameters(), lr=lr)

# Defines a BCE loss function
loss_fn = nn.BCEWithLogitsLoss()

不说了，使用前面的stepbystep的函数，可以直接

n_epochs = 100
sbs = StepByStep(model, loss_fn, optimizer)
sbs.set_loaders(train_loader, val_loader)
sbs.train(n_epochs)

需要注意的是，sigmoid函数的输入参数是(z)也就是线性的输出的结果，

结果分析

我们最后可以直接使用得到的z值来估计，如果z>0就可以认为输出为1，如果<0可以认为是0，同时我们也可以将sigmoid函数用于z，得到我们的概率输出，如果概率大于0.5则认为是1，否则为0。

混淆矩阵

决策边界，我们使用了Z=0作为边界，根据我们计算得到的w和b的权重


print(model.state_dict()))
OrderedDict([('linear.weight', tensor([[ 1.1815, -1.8690]])), ('linear.bias', tensor([-0.0581]))])

我们可以得到一个z=0的时候的的关于x2,和x1之间的关系，可以得到我们的的输出的结果，中间的白色的部分就是我们的决策边界，也可以看到最后的那个图的灰色的线，就是我们的决策线，注意这里使用的是等高线里面的0.5的时候的决策线，
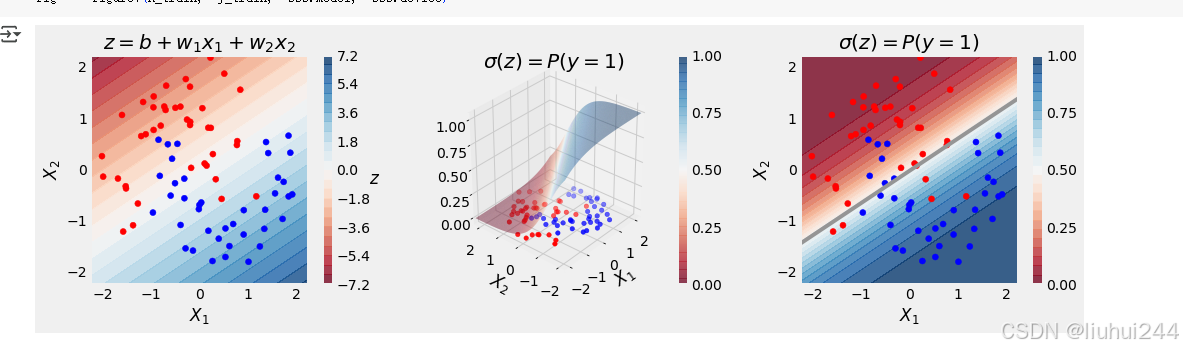
在这里插入图片描述

当然，维度越多，我们的函数的图像就可越复杂，得到我们的不同的分类的图像，例如使用的SVM支持向量机的模型，但是依然要注意我们的过渡拟合的问题，这个问题后续再说

混淆矩阵

对于概念不明白的人，大家可以看书，我这里直接使用最重要的东西，下图中的，下图中的第一和第三象限的就是我们误判的部分FP和FN，第一象限篮圈红内的点被叫做FP，因为实际是F，但是被认定为了P。所以是FP，第三现象的是FN，显然对于不同的问题我们关注的内容不同。

举个例子，我们做核酸验证，如果假阳的问题并不可怕，因为我们可以马上做第二次验证，但是如果我们的假阴性，那么就会导致传染源被遗漏，那么造成的问题就会很大。

那什么时候假阳性很可怕，原文给的是投资盈利的交易，如果假阳性，就会导致你的资金的大量的流失，导致赔钱。
在这里插入图片描述

混淆矩阵的应用应该和你具体的模型的有关系，这里使用了精确率，召回率，什么TPR，FPR的数学的内容，我觉得这个大家有需求的可以自己去学习，不是我要关注点的重点

结论

我们学习了使用BCE的损失函数和sigmoid函数来实现输出结果到概率的转换，从而实现分类的操作的行为，使用了一个新的模型的，作为了分类的实现，我们已经大概的学习了在pytorch上使用的各种的函数的实现的步骤。以及pytorch的函数的实现。这本书的卷I已经完成了，代码可以直接去看我的第0章给出的链接。