-
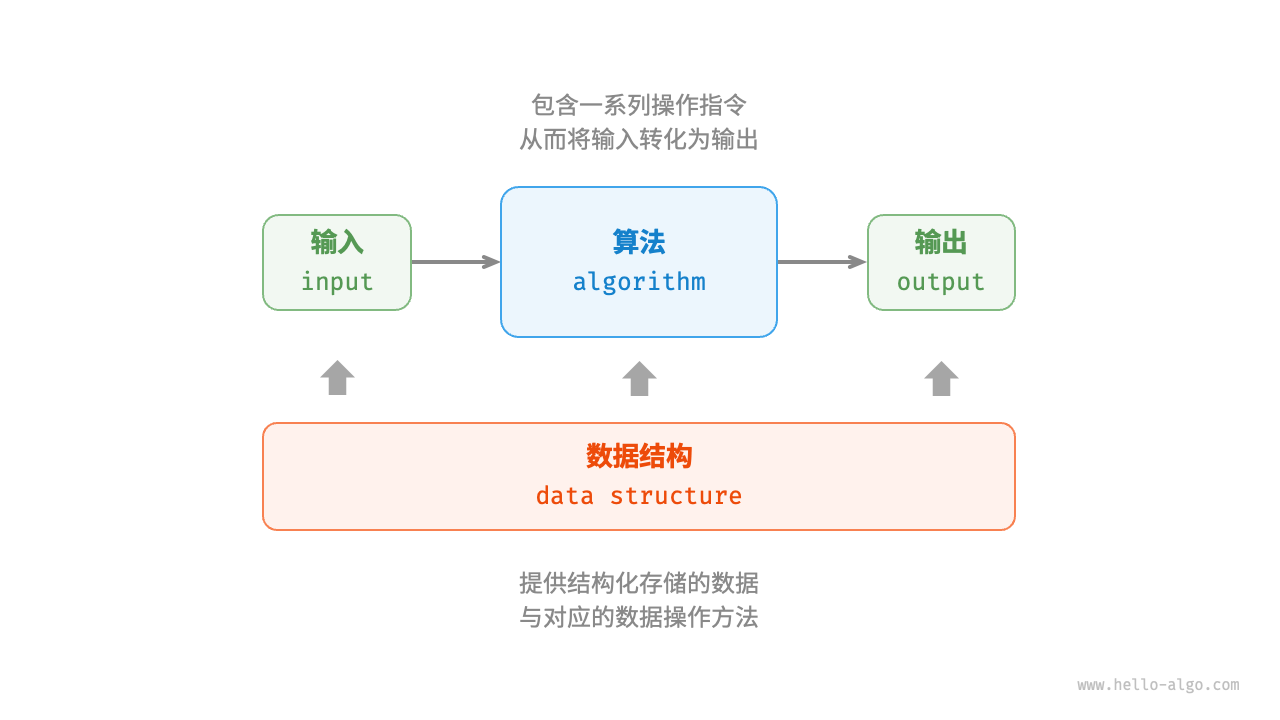
数据结构是算法的基石。数据结构为算法提供了结构化存储的数据,以及操作数据的方法。
-
算法是数据结构发挥作用的舞台。数据结构本身仅存储数据信息,结合算法才能解决特定问题。
-
算法通常可以基于不同的数据结构实现,但执行效率可能相差很大,选择合适的数据结构是关键。
>>和>>> 的区别在于是否保留符号位:
-
>>表示有符号右移。符号位会保留。
-
表示无符号右移。符号位会丢弃,用0填充。
二分法

平衡版: 向左查找和向右查找次数一致

相关算法题
1

重点:左右区间的界限
思路:确定左闭右闭1 / 左闭右开2
左闭右闭 left=0,right=mid-1 while (left <= right)左区间更新right=mid-1,右区间更新left=mid+1
左闭右开 left=0,right=mid while (left < right)左区间更新right=mid,右区间更新left=mid+1
2

int mid = low + (high - low) / 2;
优点:
-
防止溢出。如前文解释,通过减法来缩小每次计算的范围,避免产生超出整数类型最大值的情况。
-
可读性好,表达意思更清楚。
缺点:
-
需要进行除法运算,性能略差。
int mid = (low+high)>>>1;
优点:
-
性能更好,只需要加法和位运算,不需要除法。
-
Java8后,加法和位运算内部已经优化,性能比除法更好。
缺点:
-
不像减法那样有效避免溢出。当low和high较大时,有可能会溢出。
-
表达意思相对隐晦一些。
int middle = left + ((right - left) >> 1);
利用了位运算的高性能,同时通过减法来避免可能的溢出问题。表达意思也比较直白。
将middle计算放在循环内部可以保证:
-
middle始终依赖于left和right的实时值
-
每次循环都能根据middle值有效缩小左右区间进行搜索
-
避免重复计算middle,提高效率
如果将middle计算放在外面,就失去了实时反馈和依赖关系,导致搜索无法有效进行,从而出现超时。
再次强调二分搜索的核心就是根据middle不断缩小左右区间范围逼近目标值。
3

寻找target在数组里的左右边界,有如下三种情况:
-
情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
-
情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
-
情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
另一种解法及细节

在解释left - 1 >= 0 && nums[left - 1] == nums[index]这个条件判断中的一个细节。
具体来说:
-
left - 1 >= 0 是为了防止left索引减1后越界,也就是left不能为0。
-
nums[left - 1] == nums[index] 是要判断当前元素是否等于目标元素。
这里重点是两个条件的顺序不能换。
因为&&运算符是短路运算,它的计算顺序是从左到右。
如果把两个条件换个顺序写成:
nums[left - 1] == nums[index] && left - 1 >= 0
那么当left为0时,会直接因为left - 1 < 0导致条件失败,后面的nums[left - 1] == nums[index]这部分就不会执行了。
但是我们需要先检查left - 1是否越界,才能决定是否执行后面的元素比较。
4

-
设置左右边界 left=1, right=x
-
使用二分查找,每次取中间值 mid
-
判断 mid^2 是否<=x,如果是则 mid可能是结果,将 left 移到 mid+1
-
否则 mid 太大了,将 right 移到 mid-1
-
循环直到 left > right,right就是结果
-
返回结果 right
-
使用 long 来避免 int 乘法导致的溢出
5

-
设置左右边界分别为1和num
-
使用二分查找,每次取中间值mid
-
计算mid的平方square
-
如果square等于num,返回true
-
如果square小于num,则可能结果在mid右边,left移到mid+1
-
否则square大于num,结果在mid左边,right移到mid-1
-
循环直到left>right,说明没有找到,返回false
算法效率评估
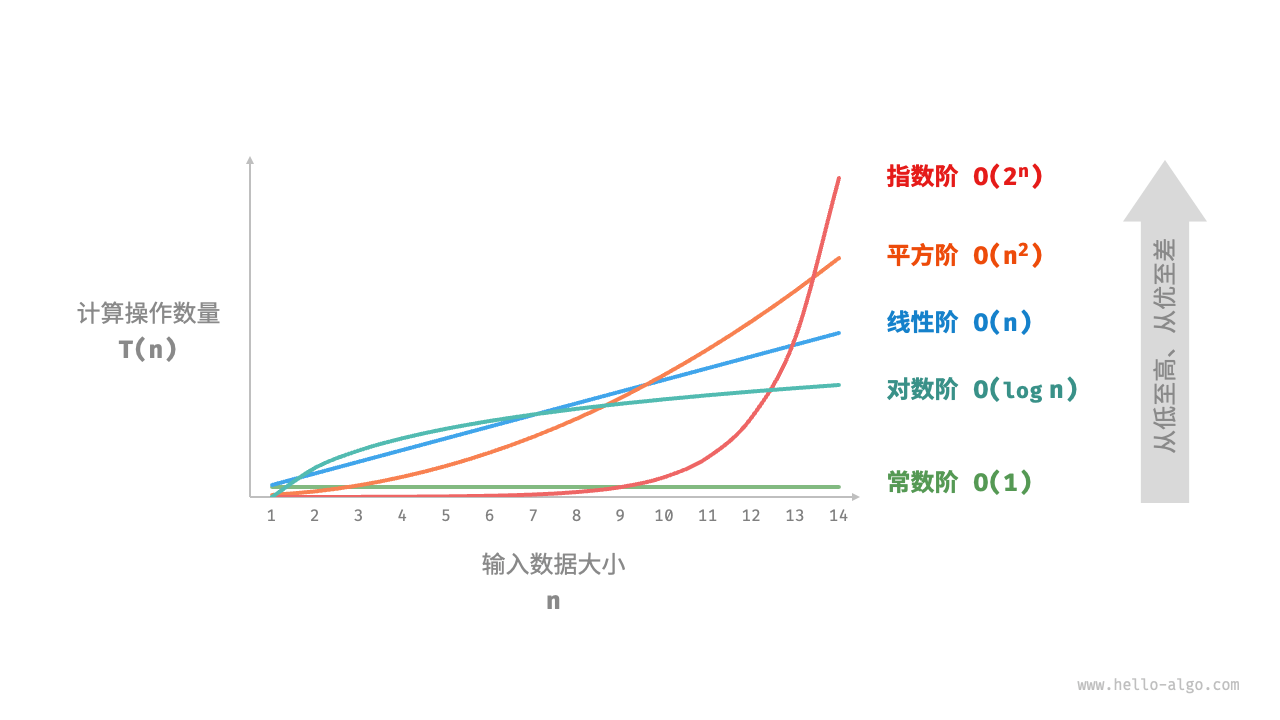
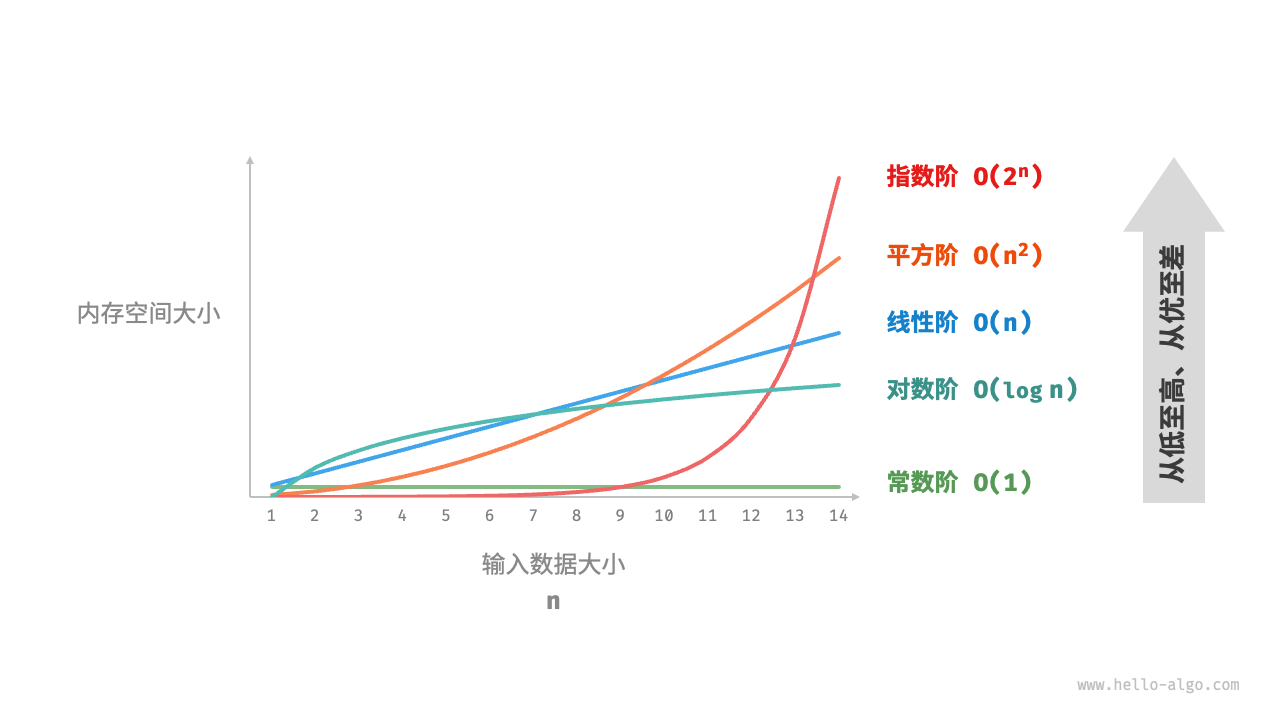
大O表示法(Big O notation)是计算复杂度理论中的一种表示法,用于描述算法运行时间或空间需求随输入规模的变化趋势。
它以最差情况下的运行时间或空间需求来估算算法的效率。具体来说:
-
O(1)表示算法的运行时间不随输入规模的增加而增加。
-
O(n)表示算法的运行时间是线性增加的,随输入规模n的增加而成正比增加。
-
O(n^2)表示算法的运行时间是平方增长的,随输入规模n的平方增加而成正比增加。
-
O(2^n)表示算法的运行时间是指数增长的。
-
O(n!)表示算法的运行时间随输入规模的阶乘而增加。
大O表示法主要考察算法随问题规模变化时的性能增长程度。它忽略了算法的细节,只关注输入规模与时间或空间需求之间的增长率。通过大O表示法可以对算法进行快速评估,并比较不同算法的效率。但它不能精确反映算法的实际运行时间。
所以,大O表示法是一种高层次的、定性的算法效率分析方法。它可以很好地描述算法效率随问题规模变化的趋势。
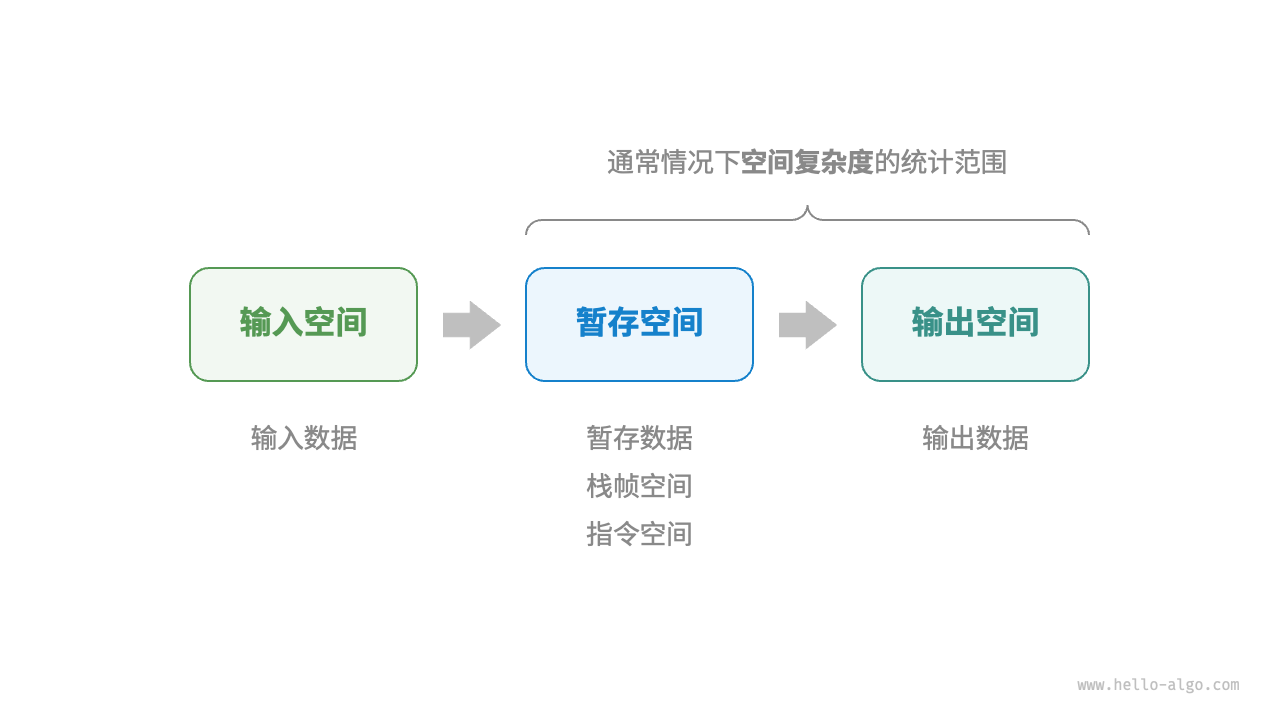
算法相关空间
-
输入空间:用于存储算法的输入数据。
-
暂存空间:用于存储算法在运行过程中的变量、对象、函数上下文等数据。
-
输出空间:用于存储算法的输出数据。
暂存空间可以进一步划分为三个部分。
-
暂存数据:用于保存算法运行过程中的各种常量、变量、对象等。
-
栈帧空间:用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧,函数返回后,栈帧空间会被释放。
-
指令空间:用于保存编译后的程序指令,在实际统计中通常忽略不计。
-
最差空间复杂度中的“最差”有两层含义。
-
以最差输入数据为准:当 n<10 时,空间复杂度为 O(1) ;但当 n>10 时,初始化的数组
nums占用 O(n) 空间,因此最差空间复杂度为 O(n) 。 -
以算法运行中的峰值内存为准:例如,程序在执行最后一行之前,占用 O(1) 空间;当初始化数组
nums时,程序占用 O(n) 空间,因此最差空间复杂度为 O(n) 。
迭代与递归
迭代
在满足一定的条件下重复执行某段代码,直到这个条件不再满足。
1.线性
-
for循环:适合在预先知道迭代次数时使用。(紧凑
-
while 循环:
while循环比for循环的自由度更高(灵活
2.n次方
-
嵌套循环
递归
通过函数调用自身来解决问题
-
递:程序不断深入地调用自身,通常传入更小或更简化的参数,直到达到“终止条件”。
-
归:触发“终止条件”后,程序从最深层的递归函数开始逐层返回,汇聚每一层的结果。
调用栈
递归函数每次调用自身时,系统都会为新开启的函数分配内存,以存储局部变量、调用地址和其他信息等。这将导致两方面的结果。
-
函数的上下文数据都存储在称为“栈帧空间”的内存区域中,直至函数返回后才会被释放。因此,递归通常比迭代更加耗费内存空间!。
-
递归调用函数会产生额外的开销。因此递归通常比循环的时间效率更低。
尾递归
-
普通递归:求和操作是在“归”的过程中执行的,每层返回后都要再执行一次求和操作。
-
尾递归:求和操作是在“递”的过程中执行的,“归”的过程只需层层返回。
递归树
区别
| 迭代 | 递归 | |
|---|---|---|
| 实现方式 | 循环结构 | 函数调用自身 |
| 时间效率 | 效率通常较高,无函数调用开销 | 每次函数调用都会产生开销 |
| 内存使用 | 通常使用固定大小的内存空间 | 累积函数调用可能使用大量的栈帧空间 |
| 适用问题 | 适用于简单循环任务,代码直观、可读性好 | 适用于子问题分解,如树、图、分治、回溯等,代码结构简洁、清晰 |
----------
数据结构
分类
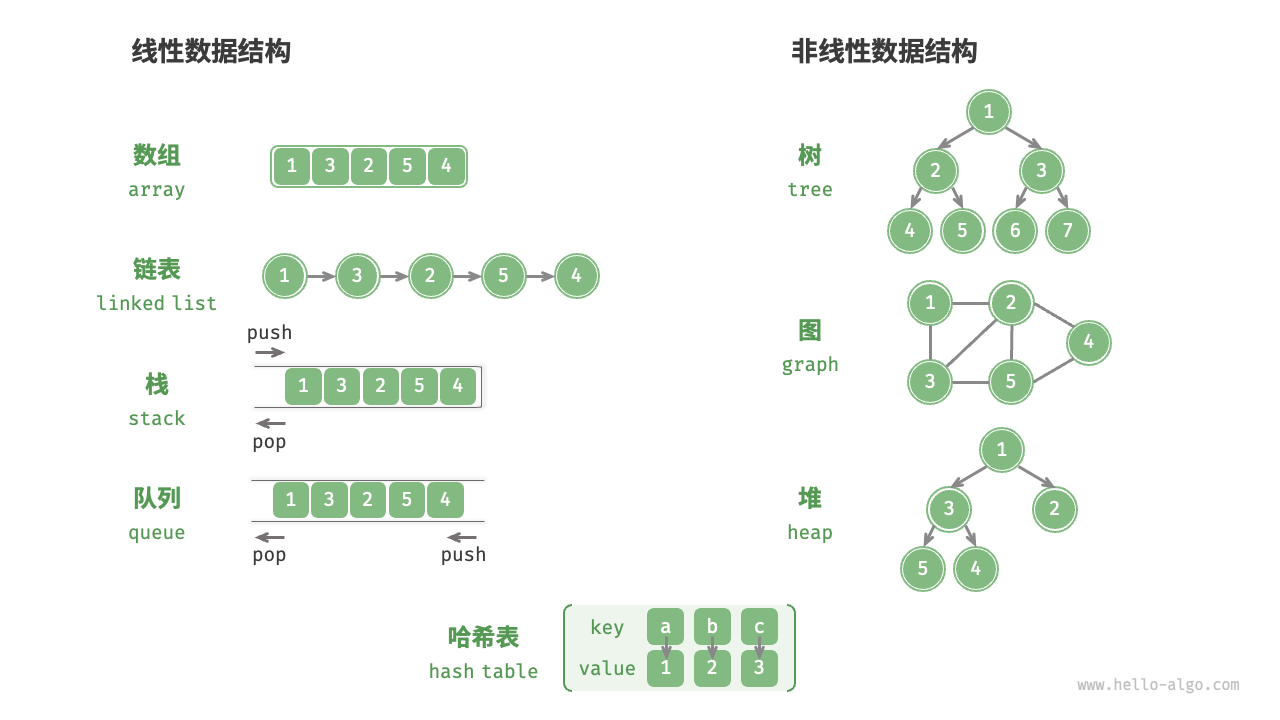
数组、链表、栈、队列、哈希表、树、堆、图,它们可以从“逻辑结构”和“物理结构”两个维度进行分类。
逻辑结构:线性与非线性
-
线性数据结构:数组、链表、栈、队列、哈希表,元素之间是一对一的顺序关系。
-
非线性数据结构:树、堆、图、哈希表。
非线性数据结构可以进一步划分为树形结构和网状结构。
-
树形结构:树、堆、哈希表,元素之间是一对多的关系。
-
网状结构:图,元素之间是多对多的关系。
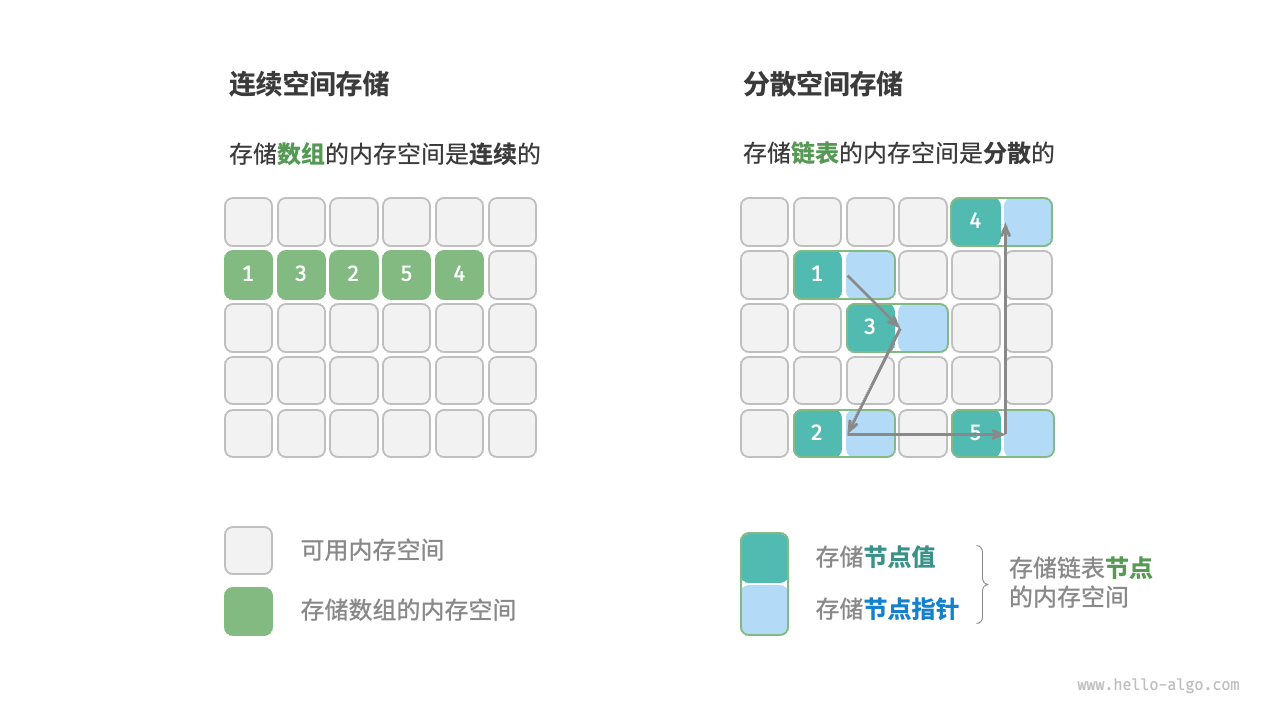
物理结构:连续与分散
内存
-
基于数组可实现:栈、队列、哈希表、树、堆、图、矩阵、张量等(“静态数据结构”)
-
基于链表可实现:栈、队列、哈希表、树、堆、图等。(“动态数据结构”)
基本数据类型
基本数据类型是 CPU 可以直接进行运算的类型。
-
整数类型
byte、short、int、long。 -
浮点数类型
float、double, -
字符类型
char,用于表示各种语言的字母、标点符号甚至表情符号等。 -
布尔类型
bool
基本数据类型以二进制的形式存储在计算机中
java情况

基本数据类型提供了数据的“内容类型”,而数据结构提供了数据的“组织方式”
-
原码、反码和补码是在计算机中编码数字的三种方法,它们之间可以相互转换。整数的原码的最高位是符号位,其余位是数字的值。
-
整数在计算机中是以补码的形式存储的。在补码表示下,计算机可以对正数和负数的加法一视同仁,不需要为减法操作单独设计特殊的硬件电路,并且不存在正负零歧义的问题。
-
浮点数的编码由 1 位符号位、8 位指数位和 23 位分数位构成。由于存在指数位,因此浮点数的取值范围远大于整数,代价是牺牲了精度。
-
ASCII 码是最早出现的英文字符集,长度为 1 字节,共收录 127 个字符。
-
GBK 字符集是常用的中文字符集,共收录两万多个汉字。
-
Unicode 致力于提供一个完整的字符集标准,收录世界上各种语言的字符,从而解决由于字符编码方法不一致而导致的乱码问题。
-
UTF-8 是最受欢迎的 Unicode 编码方法,通用性非常好。它是一种变长的编码方法,具有很好的扩展性,有效提升了存储空间的使用效率。UTF-16 和 UTF-32 是等长的编码方法。在编码中文时,UTF-16 占用的空间比 UTF-8 更小。Java 和 C# 等编程语言默认使用 UTF-16 编码。
提问
Q:为什么哈希表同时包含线性数据结构和非线性数据结构?
哈希表底层是数组,而为了解决哈希冲突,我们可能会使用“链式地址” 数组中每个桶指向一个链表,当链表长度超过一定阈值时,又可能被转化为树(通常为红黑树)。
从存储的角度来看,哈希表的底层是数组,其中每一个桶槽位可能包含一个值,也可能包含一个链表或一棵树。因此,哈希表可能同时包含线性数据结构(数组、链表)和非线性数据结构(树)。
Q:char 类型的长度是 1 字节吗?
char 类型的长度由编程语言采用的编码方法决定。例如,Java、JavaScript、TypeScript、C# 都采用 UTF-16 编码(保存 Unicode 码点),因此 char 类型的长度为 2 字节。
Q:基于数组实现的数据结构也称“静态数据结构” 是否有歧义?栈也可以进行出栈和入栈等操作,这些操作都是“动态”的。
栈确实可以实现动态的数据操作,但数据结构仍然是“静态”(长度不可变)的。尽管基于数组的数据结构可以动态地添加或删除元素,但它们的容量是固定的。如果数据量超出了预分配的大小,就需要创建一个新的更大的数组,并将旧数组的内容复制到新数组中。
Q:在构建栈(队列)的时候,未指定它的大小,为什么它们是“静态数据结构”呢?
在高级编程语言中,我们无须人工指定栈(队列)的初始容量,这个工作由类内部自动完成。例如,Java 的 ArrayList 的初始容量通常为 10。另外,扩容操作也是自动实现的。
数组
线性数据结构
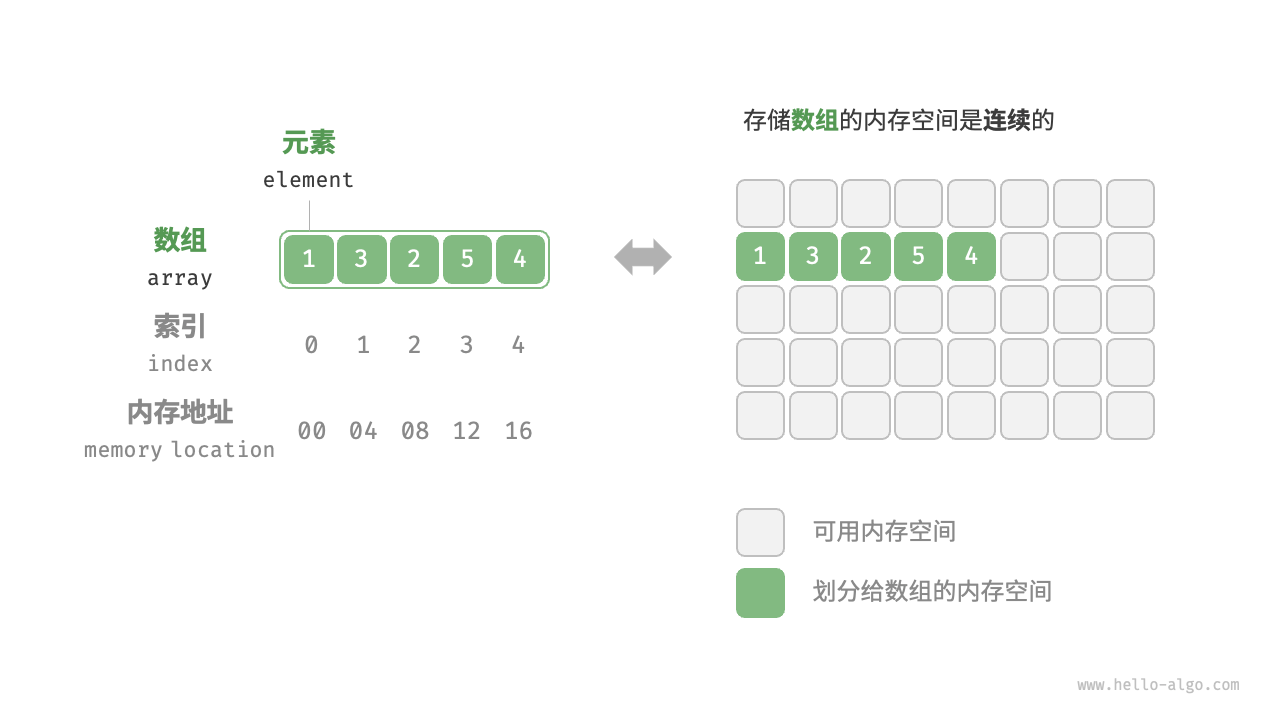
两种初始化方式:无初始值、给定初始值
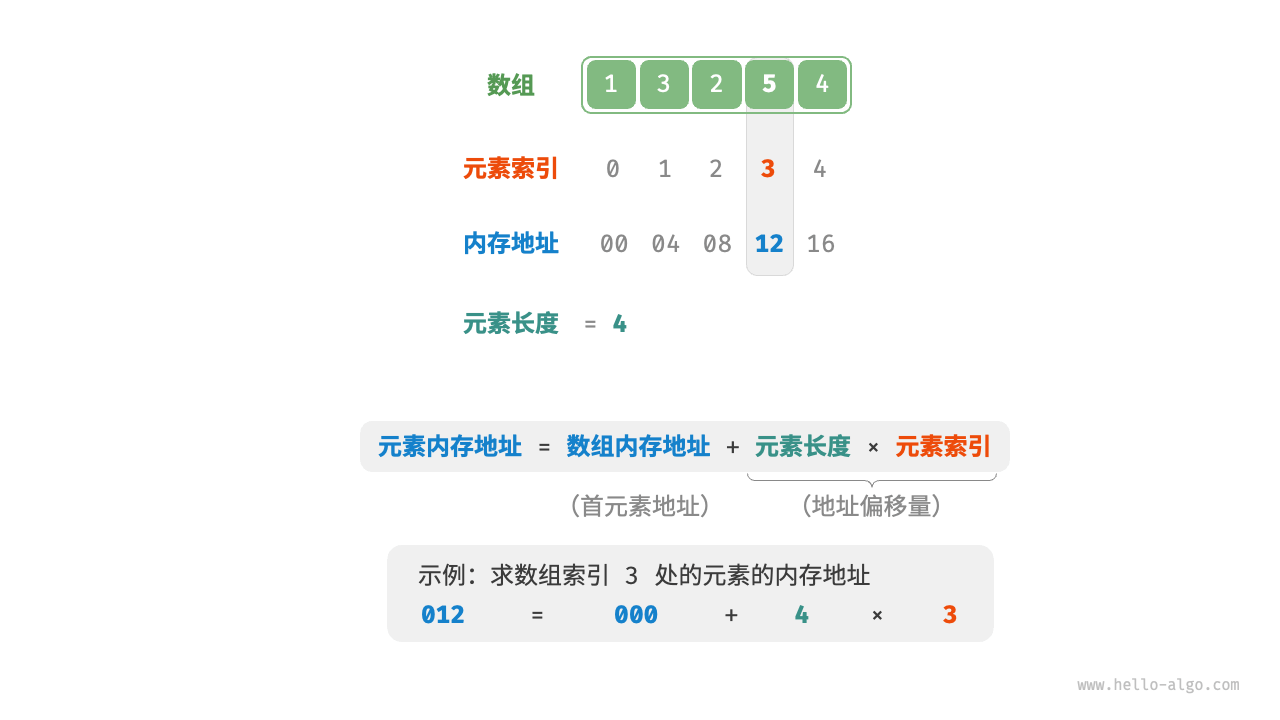
索引本质上是内存地址的偏移量因此首个元素索引为 0 是合理的
数组的插入与删除操作有以下缺点。
-
时间复杂度高:数组的插入和删除的平均时间复杂度均为 O(n) ,其中n 为数组长度。
-
丢失元素:由于数组的长度不可变,因此在插入元素后,超出数组长度范围的元素会丢失。
-
内存浪费:我们可以初始化一个比较长的数组,只用前面一部分,这样在插入数据时,丢失的末尾元素都是“无意义”的,但这样做会造成部分内存空间浪费。
二分法
重点:左右区间的界限

平衡版: 向左查找和向右查找次数一致

1

思路:确定左闭右闭1 / 左闭右开2
左闭右闭 left=0,right=mid-1 while (left <= right)左区间更新right=mid-1,右区间更新left=mid+1
左闭右开 left=0,right=mid while (left < right)左区间更新right=mid,右区间更新left=mid+1
2

int mid = low + (high - low) / 2;
优点:
-
防止溢出。如前文解释,通过减法来缩小每次计算的范围,避免产生超出整数类型最大值的情况。
-
可读性好,表达意思更清楚。
缺点:
-
需要进行除法运算,性能略差。
int mid = (low+high)>>>1;
优点:
-
性能更好,只需要加法和位运算,不需要除法。
-
Java8后,加法和位运算内部已经优化,性能比除法更好。
缺点:
-
不像减法那样有效避免溢出。当low和high较大时,有可能会溢出。
-
表达意思相对隐晦一些。
int middle = left + ((right - left) >> 1);
利用了位运算的高性能,同时通过减法来避免可能的溢出问题。表达意思也比较直白。
将middle计算放在循环内部可以保证:
-
middle始终依赖于left和right的实时值
-
每次循环都能根据middle值有效缩小左右区间进行搜索
-
避免重复计算middle,提高效率
如果将middle计算放在外面,就失去了实时反馈和依赖关系,导致搜索无法有效进行,从而出现超时。
再次强调二分搜索的核心就是根据middle不断缩小左右区间范围逼近目标值。
3

寻找target在数组里的左右边界,有如下三种情况:
-
情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
-
情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
-
情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
另一种解法及细节

在解释left - 1 >= 0 && nums[left - 1] == nums[index]这个条件判断中的一个细节。
具体来说:
-
left - 1 >= 0 是为了防止left索引减1后越界,也就是left不能为0。
-
nums[left - 1] == nums[index] 是要判断当前元素是否等于目标元素。
这里重点是两个条件的顺序不能换。
因为&&运算符是短路运算,它的计算顺序是从左到右。
如果把两个条件换个顺序写成:
nums[left - 1] == nums[index] && left - 1 >= 0
那么当left为0时,会直接因为left - 1 < 0导致条件失败,后面的nums[left - 1] == nums[index]这部分就不会执行了。
但是我们需要先检查left - 1是否越界,才能决定是否执行后面的元素比较。
4

-
设置左右边界 left=1, right=x
-
使用二分查找,每次取中间值 mid
-
判断 mid^2 是否<=x,如果是则 mid可能是结果,将 left 移到 mid+1
-
否则 mid 太大了,将 right 移到 mid-1
-
循环直到 left > right,right就是结果
-
返回结果 right
-
使用 long 来避免 int 乘法导致的溢出
5

-
设置左右边界分别为1和num
-
使用二分查找,每次取中间值mid
-
计算mid的平方square
-
如果square等于num,返回true
-
如果square小于num,则可能结果在mid右边,left移到mid+1
-
否则square大于num,结果在mid左边,right移到mid-1
-
循环直到left>right,说明没有找到,返回false
移除元素
双指针法
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
重点:理解快慢指针
-
快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
-
慢指针:指向更新 新数组下标的位置

1

2

-
使用两个指针 i 和 j
-
i 用于遍历整个数组
-
如果nums[i] != 0,就将nums[i]的值赋给nums[j],然后同时将i和j向后移一位
-
这样可以保证从索引0到j-1位置的元素都是非零元素
-
当i遍历完整个数组后,j指向的位置就是第一个零元素应该出现的位置
-
将剩余位置从j到n-1全部置为0
3

4
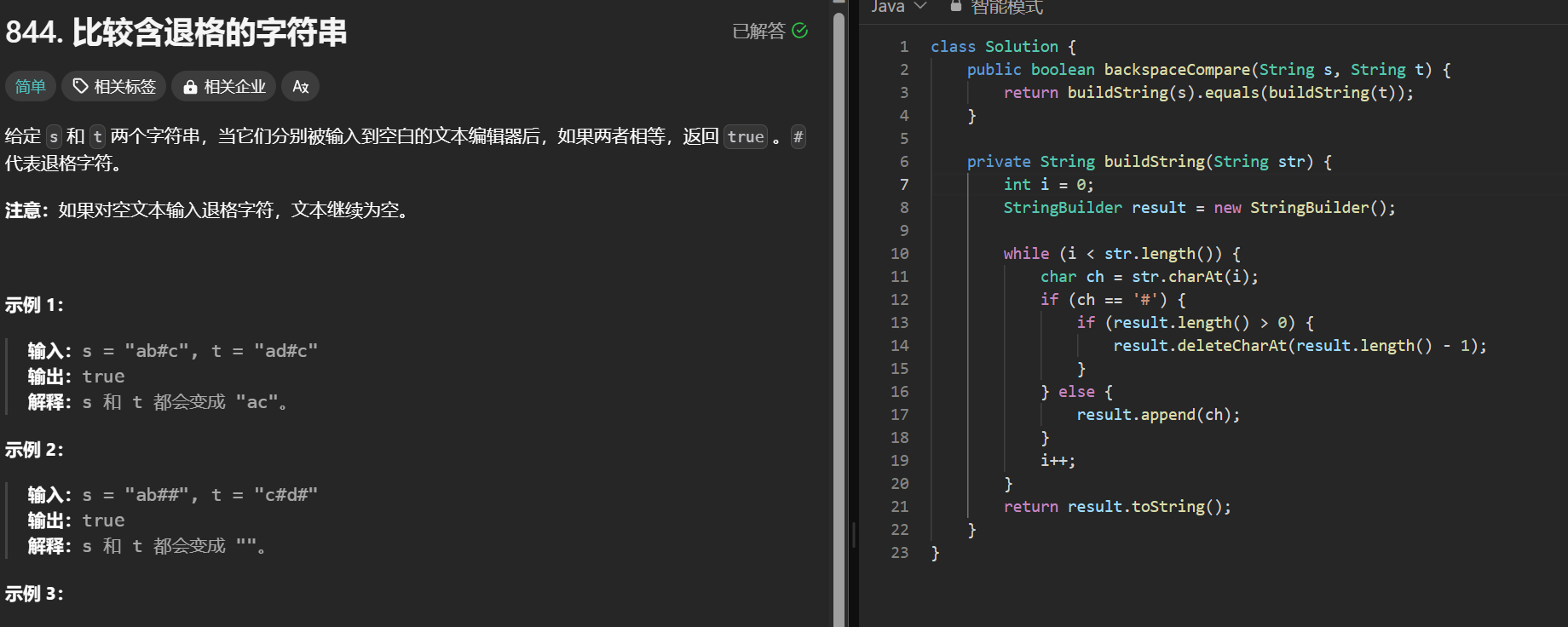
滑动窗口
1.最小滑窗
while j < len(nums): 判断[i, j]是否满足条件 while 满足条件: 不断更新结果(注意在while内更新!) i += 1 (最大程度的压缩i,使得滑窗尽可能的小) j += 1

-先思考
-
窗口内是什么?
-
如何移动窗口的起始位置?
-
如何移动窗口的结束位置?
对于这道题
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
2.最大滑窗
while j < len(nums): 判断[i, j]是否满足条件 while 不满足条件: i += 1 (最保守的压缩i,一旦满足条件了就退出压缩i的过程,使得滑窗尽可能的大) 不断更新结果(注意在while外更新!) j += 1

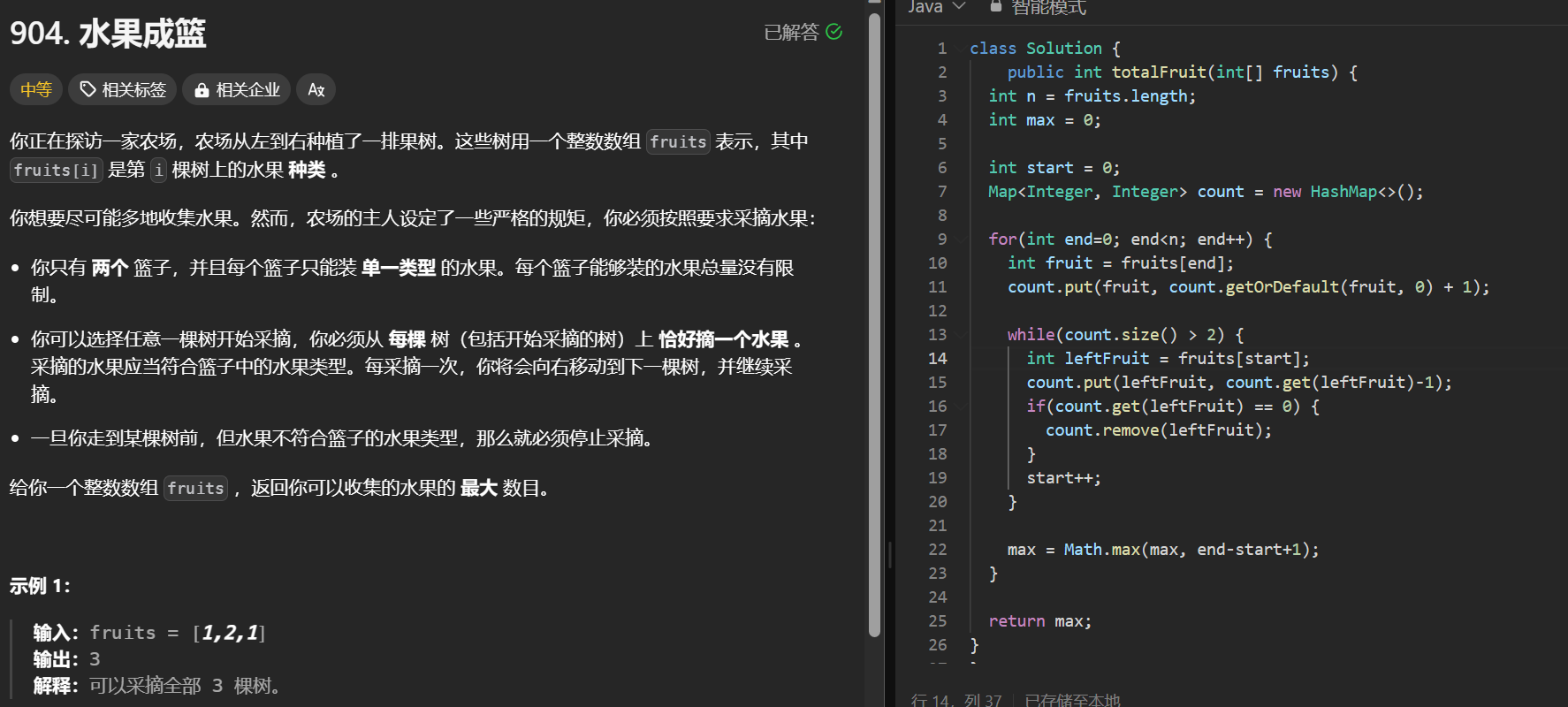
count.put(fruit, count.getOrDefault(fruit, 0) + 1);
统计fruit出现的次数,如果之前没有统计过这个fruit,则记为1,如果有则value值加1。
while(count.size() > 2) {
int leftFruit = fruits[left];
count.put(leftFruit, count.get(leftFruit)-1);
..... }
统计fruits数组中的元素出现次数,每移动一次left索引,对应元素的计数会减1,如果计数减到0,则从统计结果map中移除这个元素。
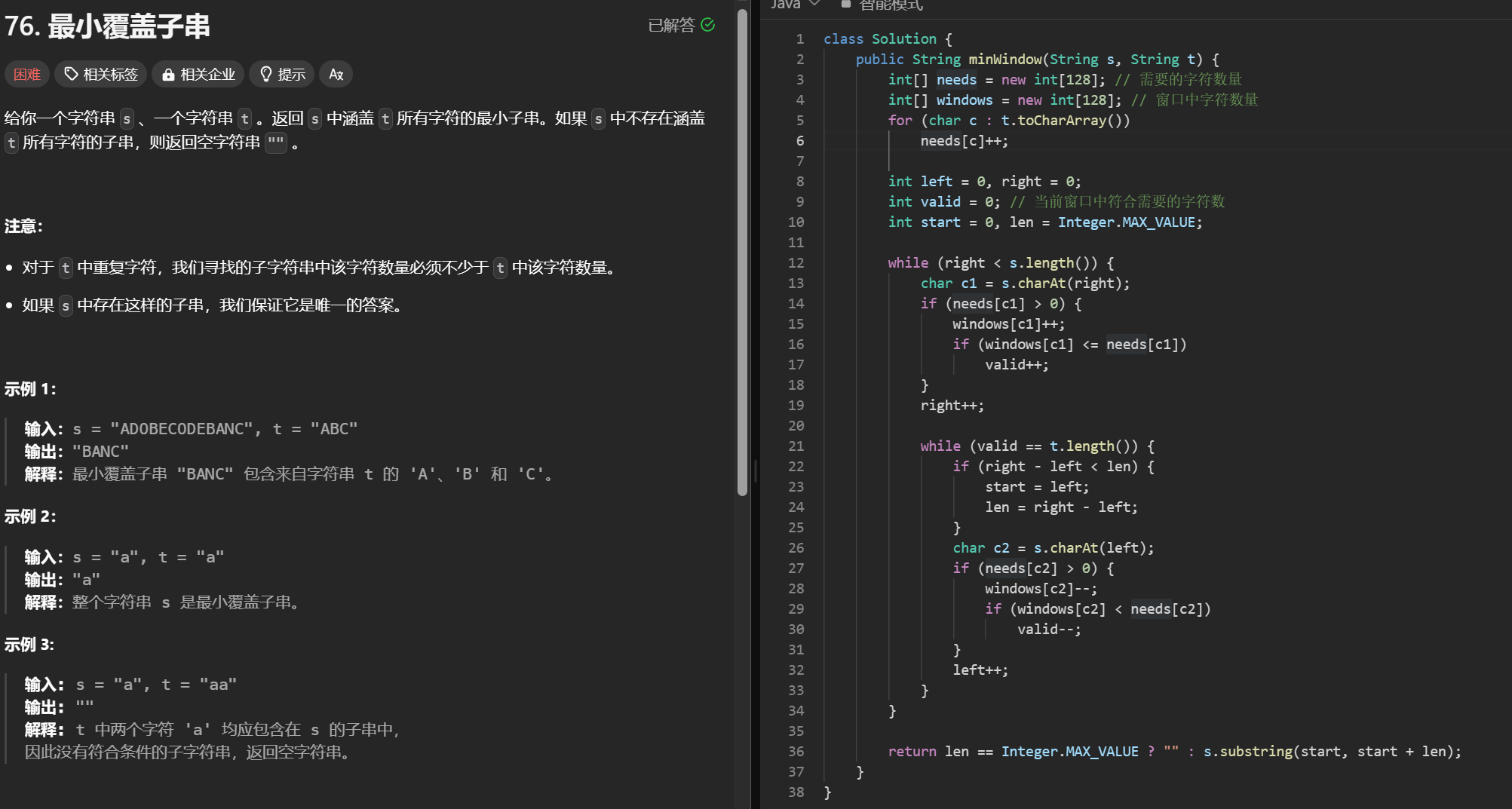
如果needs[c1]>0,表示c1是t需要的字符
则windows[c1]++,增加窗口内c1的计数
如果增加后windows[c1]<=needs[c1],表示窗口内c1的数量满足需求
则valid++
这里是增加窗口时,增加字符后检查是否满足需求。
-
如果needs[c2]>0,表示c2是t需要的字符
则windows[c2]--,减少窗口内c2的计数
如果减少后windows[c2]<needs[c2],表示窗口内c2的数量不再满足需求
则valid--
这里是减少窗口时,减少字符后检查是否不再满足需求。
区别在于:
增加窗口时,增加字符后检查是否满足需求
减少窗口时,减少字符后检查是否不再满足需求
一个是增加后检查,一个是减少后检查,目的都是为了正确记录valid计数,知道窗口内字符数量是否满足t的需求。
区别
最大滑窗是在迭代右移右边界的过程中更新结果,而最小滑窗是在迭代右移左边界的过程中更新结果。
螺旋矩阵
class Solution {
public int[][] generateMatrix(int n) {
int loop = 0; // 控制循环次数
int[][] res = new int[n][n];
int start = 0; // 每次循环的开始点(start, start)
int count = 1; // 定义填充数字
int i, j;
while (loop++ < n / 2) { // 判断边界后,loop从1开始
// 模拟上侧从左到右
for (j = start; j < n - loop; j++) {
res[start][j] = count++;
}
// 模拟右侧从上到下
for (i = start; i < n - loop; i++) {
res[i][j] = count++;
}
// 模拟下侧从右到左
for (; j >= loop; j--) {
res[i][j] = count++;
}
// 模拟左侧从下到上
for (; i >= loop; i--) {
res[i][j] = count++;
}
start++;
}
if (n % 2 == 1) {
res[start][start] = count;
}
return res;
}
}
边界左闭右开
循环不变量原则:
-
对于任何循环,都应该定义一个循环不变量。循环不变量是指在循环的每一次迭代入口都应该成立的条件。
-
循环体内的代码应该保持循环不变量的正确性。也就是说,循环体内应该对循环状态进行必要的修改,以确保循环结束后循环不变量依然成立。
-
循环条件应该依赖于循环不变量。也就是说,循环只有在不满足循环不变量时才继续执行。
通过定义并维护循环不变量,可以帮助设计和理解循环的正确性。它有以下几个好处:
-
明确定义循环的目的和边界条件。
-
简化循环内部代码的理解和调试。
-
循环结束时可以直接验证结果是否正确。
-
当循环条件或循环体发生变化时,通过检查不变量是否依然成立可以帮助验证修改是否正确。
总之,循环不变量原则通过定义明确的不变量条件,有效地约束和控制循环的设计,从而提高循环代码的可读性、可维护性和正确性。它是设计循环时一个重要的最佳实践。
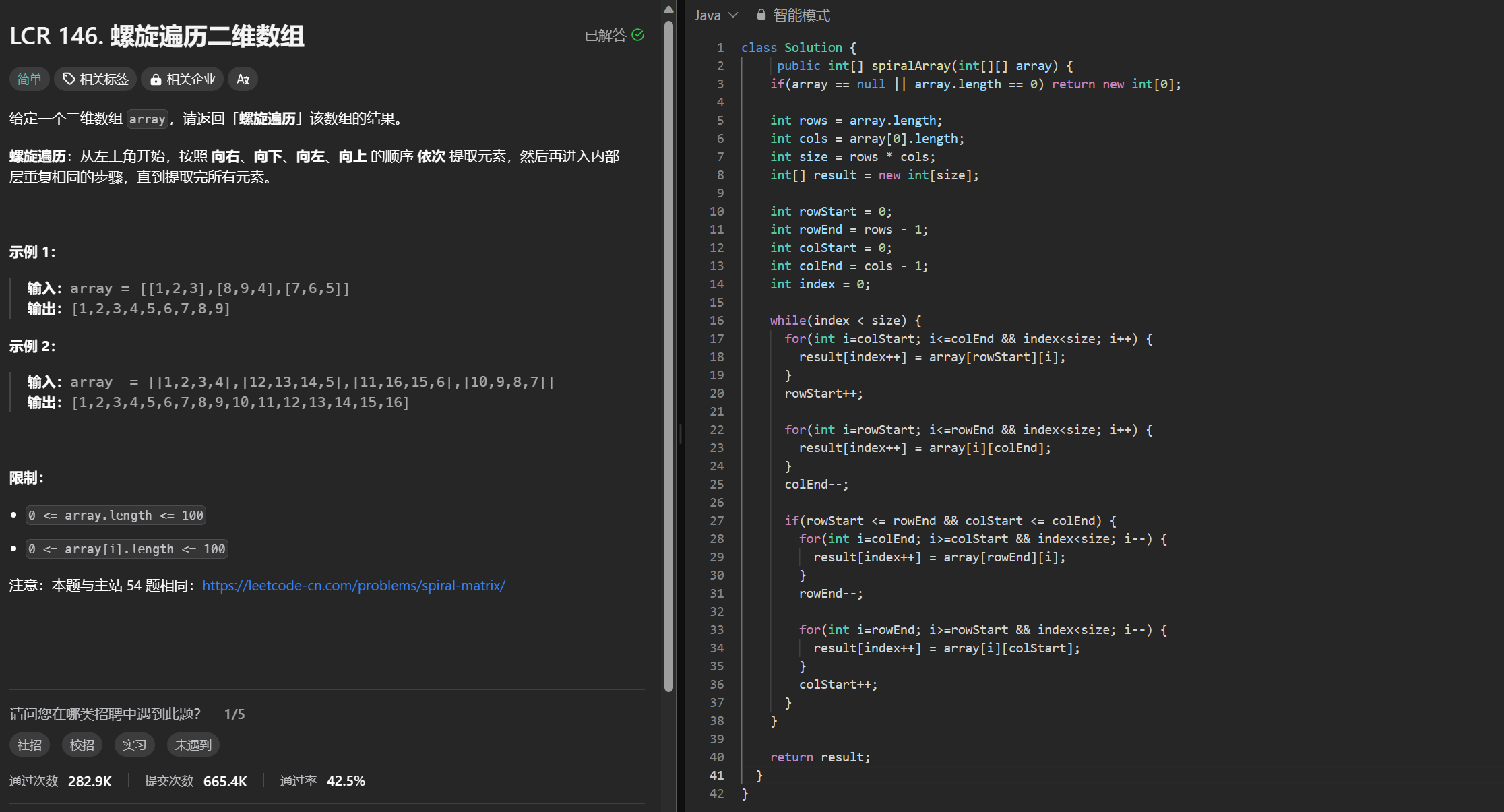
主要思路:
-
使用循环变量index记录一维数组索引
-
在每轮螺旋中提取元素赋值到result数组
-
每轮更新行列边界值rowStart/End, colStart/End
-
终止条件是index>=size或者越过边界




 本文围绕Java展开,介绍算法与数据结构相关知识。算法方面,阐述二分法、迭代与递归,还提及算法效率评估;数据结构方面,讲解分类、逻辑与物理结构,以及数组等。此外,还介绍移除元素的双指针法、滑动窗口和螺旋矩阵的循环不变量原则。
本文围绕Java展开,介绍算法与数据结构相关知识。算法方面,阐述二分法、迭代与递归,还提及算法效率评估;数据结构方面,讲解分类、逻辑与物理结构,以及数组等。此外,还介绍移除元素的双指针法、滑动窗口和螺旋矩阵的循环不变量原则。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








