看博客总结出来的图【数据结构】

写在开头： 文章借鉴于他人博客，加上了一些细节

一、图的定义

图(Graph)G由两个集合V和E组成，记为G=(V,E),其中V是顶点的有穷非空集合,E是V中顶点的边的有穷集合。

有向图： 顶点之间的边有方向，有向边也叫做弧，起点叫做弧尾，终点叫做弧头。

无向图： 顶点之间的边没有方向。

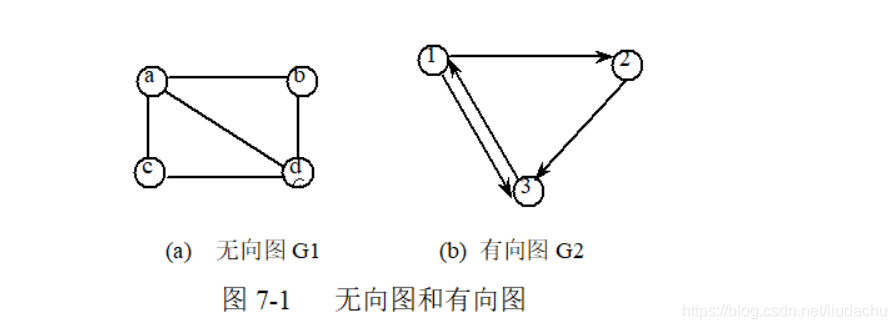
二、图的基本术语

无向完全图： 无向图中，任意两个顶点之间都存在边，有n(n-1) 条边。

有向完全图： 有向图中，任意两个顶点之间都存在方向互为相反的两条弧，有n(n-1) 条弧。

权 每条边上具有的含有某种特殊含义的数值，叫做边上的权。

网： 带权的图称为网 。

邻接点： 对于一条边上两个顶点，称这两个顶点互为邻接点，边依附于这两个顶点，或者与这两个顶点相关联。

顶点的度： 和顶点相关联的边的数目。

顶点的入度： 以该顶点为弧头的弧的数目。(指向顶点的弧的数目)

顶点的出度： 以该顶点为弧尾的弧的数目。(以顶点为起点的弧的数目)

路径： 两个顶点之间顶点的序列。

路径长度： 路径上经过的边或者弧的数目。

回路(回环)： 第一个顶点和最后一个顶点相同的路径。

简单路径： 路径序列中的顶点不重复出现的路径。

简单回路： 路径序列中的顶点不重复出现的回路。

连通(无向图)： 无向图中两个顶点之间有路径称这俩顶点时连通的

连通图： 图中任意两个顶点都是连通的。

连通分量： 非连通图中的极大连通子图**。

连通图的生成树： 无向图中连通且n个顶点n-1条边叫生成树。

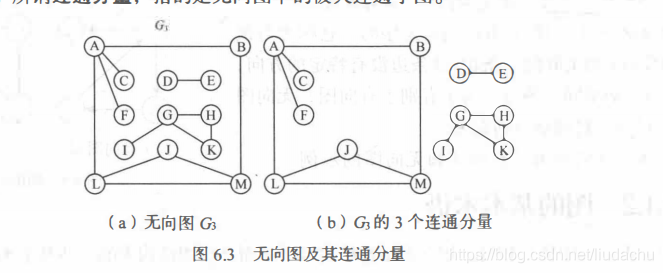
强连通图(有向图)： 有向图中，对于每一对顶点a和b，从a到b和从b到a都有路径，成为强连通图。

强连通分量： 有向图的极大强连通子图。

有向树： 一顶点入度为0其余顶点入度为1的有向图。

非连通图的生成森林： 由非连通图的连通分量的生成树组成。

三、图的存储结构

[图解部分来自百度]

1.邻接矩阵：
用两个数组，一个数组保存顶点集，一个数组保存边集。

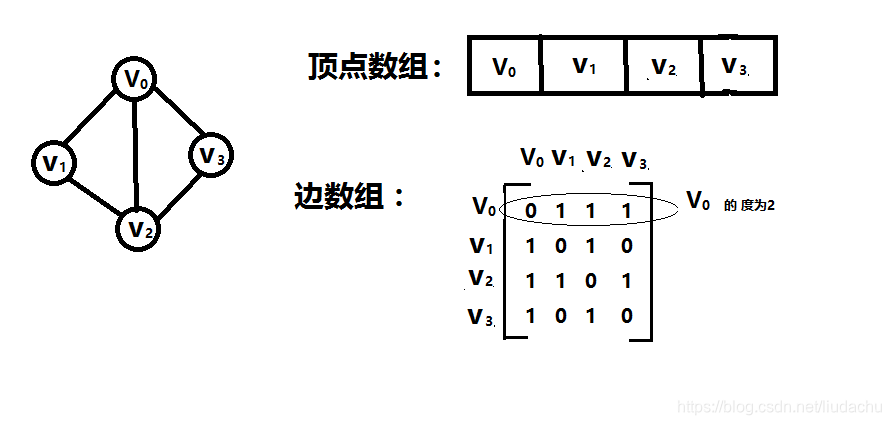
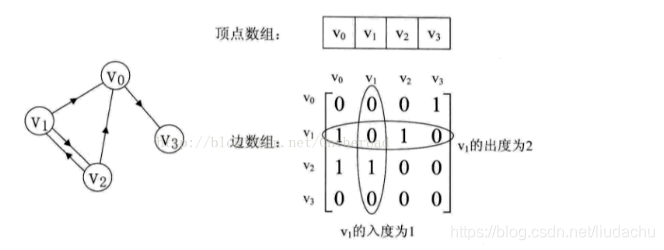
//---------图的邻接矩阵存储表示------

#define maxvex 100   //最大顶点数
typedef struct{
	char vexs[maxvex];    //顶点数组(假设顶点为char类型)
	int arc[maxvex][maxvex]; //边数组(邻接矩阵)
	int vertex,edges;    //图当前的点数和边数
}MGraph;   //定义图

创建无向图：

#define maxvexs 100
#define infinity 65535//用65535来表示∞
typedef struct
{
    char vexs[maxvexs];
    int arc[maxvexs][maxvexs];
    int vertexes,edges;
}mgraph;

void creatgraph(mgraph &g)
{
    int i,j,k,w;
    printf("输入顶点数和边数:\n");
    scanf("%d,%d",&g.vertexes,&g.edges);
    for(i=0;i<g->vertexes;i++)
        scanf("%c",&g->vexs[i]);//读入顶点信息，建立顶点表
        
    for(i=0;i<g->vertexes;i++)
        for(j=0;j<g->vertexes;j++)
            g->arc[i][j]=infinity;//初始化邻接矩阵
            
    for(k=0;k<g->vertexes;k++)//读入edges条边，建立邻接矩阵
    {
        printf("输入边(Vi,vj)上的下标i，下标j,和权w:\n");
        scanf("%d%d%d",&i,&j,&w);
        g.arc[i][j]=w;
        g.arc[j][i]=w;//无向图，矩阵对称
    }
}

［算法分析］

优点：
1.便于判断两个顶点之间是否有边。
2.便于计算各个顶点的度。

缺点：
1.不便于增加和删除顶点。
2.不便于统计边的数目，需要扫描邻接矩阵所有元素。
3.空间复杂度高。

2.邻接表：
用两个表，表头结点表，边表。（数组与链表相结合的存储方法）

表头结点表： 由所有表头结点以顺序结构的形式存储，以便可以随机访问任一顶点的边链表。
边表： 由表示图中顶点间关系的 2n个边链表组成。 边链表中边结点包括邻接点域(adjvex)、数据域 (info) 和链域 (nextarc) 三部分， 如图所示。

无向图的邻接表表示

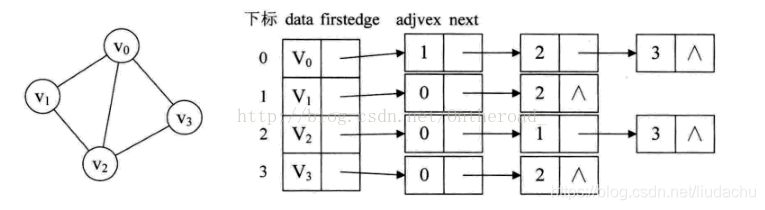
对于带权值的网图，可以在边表结点定义中再增加一个weight的数据域，存储权值信息即可。

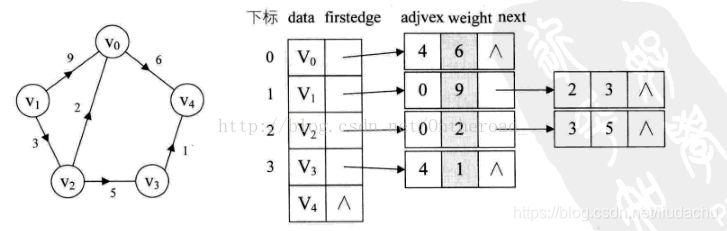
邻接表结点的定义

#define MVNum 100   //最大顶点数
typedef struct EdgeNode//边表结点
{
    int adjvex; //邻接点域，存储该顶点对应的下标
    int weight; //用于存储权值，对于非网图可以不需要
    struct EdgeNode *next;  //链域，指向下一个邻接点
}EdgeNode;
 
typedef struct VertexNode //顶点表结点
{
    char data; //顶点域，存储顶点信息
    EdgeNode *firstedge; //边表头指针
}VertexNode,AdjList[MAXVEX];  //AdjList表示邻接表类型
 
typedef struct
{
    AdjList adjList;    //邻接表
    int numVertexes,numEdges;//图中当前顶点数和边数
}GraphAdjList;          //定义图
 

[算法分析]

该算法的时间复杂度是O(n + e)。
该算法的空间复杂度为 O(n + e)。

优点：
1.便于增加和删除顶点
2.便于统计边的数目，时间复杂度为O(n+e)。
3.空间效率高，空间复杂度为 O(n + e)。
缺点：
1.不便于判断顶点之间是否有边
2.不便于计算有向图各个顶点的度。

3. 十字链表

• 十字链表：容易操作，复杂度与邻接表相似。

4. 邻接多重表

• 邻接多重表：容易操作，复杂度与邻接表相似。

四、图的遍历

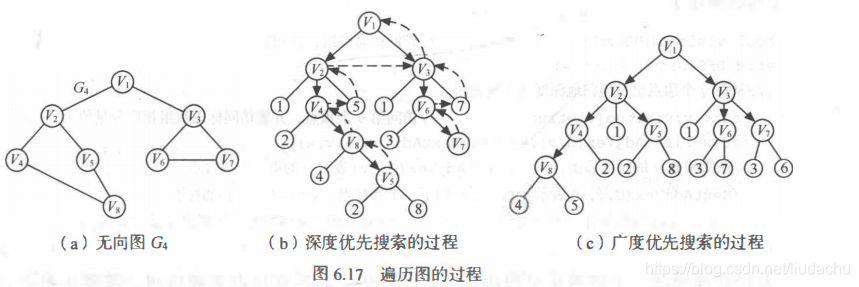
1.深度优先搜索(DFS): 和树的遍历类似，图的遍历也是从图中某一顶点出发，按照某种方法对图中所有顶点访问且仅访问一次。

【算法步骤】

1.从图中某个顶点v出发,访问v,。
2.找出刚被访问过的顶点的第一个未被访问的邻接点，访问该顶点。以该顶点作为新顶点，重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止。
3.返回前一个访问过的顶点且仍有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的邻接点，访问该顶点。
4.重复步骤2和3，直至图中所有顶点都被访问过，搜索结束。

【算法实现】

void DFS(Vertex V){
   visit[V]=true;
   for(V 的每个邻接点 W)
      for(!visit[W])
         DFS(W);
}

2.广度优先遍历（BFS）： 类似于树的层次遍历。

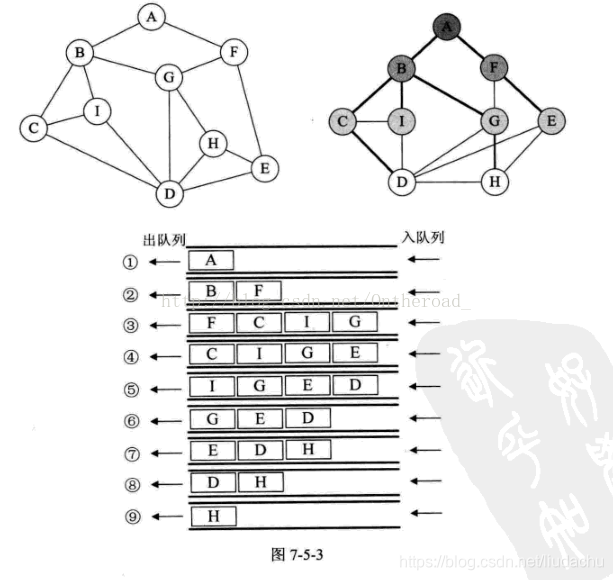
【算法步骤】
1.从图中某个顶点v出发，访问v，并置visis[v]的值为true,然后将v进队。
2.只要队列不空，则重复一下操作：
(1)队列顶点u出队
(2)依次检查u的所有邻接点w,如果visited[w]的值为false,则访问w,并置visted[w]的值为true.然后将w进队。

void BFS(Vertex V){
   visited[V]=true;
   Enqueue(V,Q);   //顶点入队
   while(!IsEmpty(Q)){
     V=Dequeue(Q);  //出队
     for(V 的每个邻接点 W)
       if(!visited[W]){
         visited[W]=true;
         Enqueue(W,Q);  //新顶点入队
       }
   }
}

五、最小生成树

最小生成树： 在一个连通网的所有生成树中，各边的代价之和最小的那棵生成树称为该连通网的最小代价生成树 (Minimum Cost Spanning Tree), 简称为最小生成树。

连通网： 带权的连通图。
代价： 权值

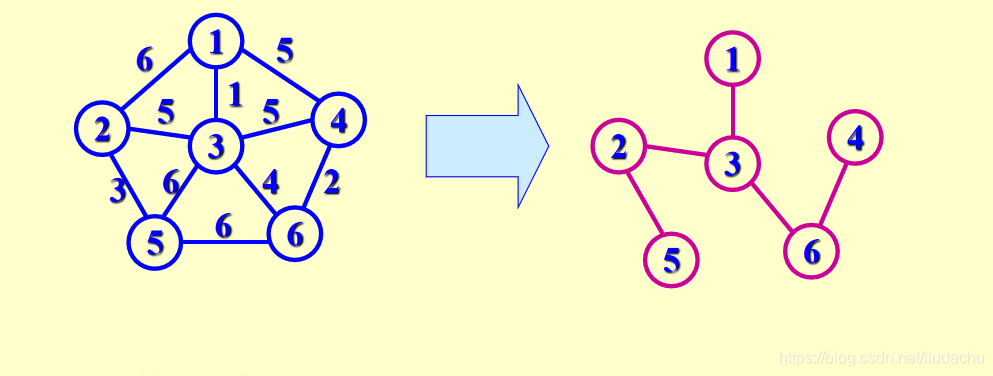
1.普里姆(prime)算法:

【算法步骤】

先将一个起点加入最小生成树，之后不断寻找与最小生成树相连的边权最小的边能通向的点，并将其加入最小生成树，直至所有顶点都在最小生成树中。

【算法效率分析】

Prim算法的时间效率＝O（n2）  
Prim算法是归并顶点，适用于稠密网。

2.克鲁斯卡尔（kluskal) 算法:

【算法步骤】

在剩下的所有未选取的边中，找最小边，如果和已选取的边构成回路，则放弃，选取次小边。

【算法效率分析】
算法的时间效率＝O（elog2e）
Kruskal算法是归并边，适用于稀疏图（用邻接表）

六、拓扑排序与关键路径

有向无环图的概念

① AOE网(Activity On Edges)—用边表示活动的网络
AOE网定义：在带权有向无环网中， 用有向边表示一个工程中的活动，用边上权值表示活动持续时间，用顶点表示事件，则这样的有向图叫做用边表示活动的网络，简称 AOE。

② AOV网(Activity On Vertices)—用顶点表示活动的网络
AOV网定义：若用有向图表示一个工程，在图中用顶点表示活动，用弧表示活动间的优先关系。Vi 必须先于活动Vj 进行。则这样的有向图叫做用顶点表示活动的网络，简称 AOV

拓扑排序

检查有向图中是否存在回路的方法之一，是对有向图进行拓扑排序。

拓扑排序(topologicalsort)是将AOV网中的各个顶点排成一个有序序列，使得所有的前驱和后继关系都能得到满足。

【拓扑排序步骤】

从有向图中选取一个没有前驱的顶点(入度为零的顶点)，并输出之;
从有向图中删去此顶点以及所有以它为尾的弧。(弧头顶点的入度减1)

关键路径

因AOV网中的活动可以并行，故工程完成的最短时间为从源点到汇点的最长路径(关键路径)。

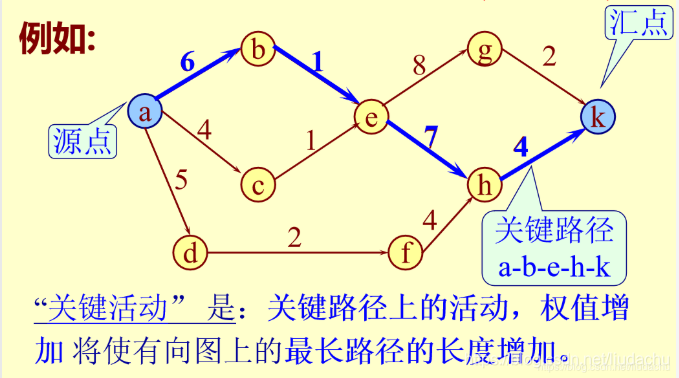
活动的最早发生时间

把从源点到顶点j的最长路径长度叫做事件(顶点) 的 最早发生时间ve(j);

活动的最迟发生时间

把从顶点k到汇点的最短路径长度叫做事件(顶点) 的 最迟发生时间 vl(k) .

关键活动:

最早开始时间=最迟开始时间

七、最短路径

1.迪杰斯算法(Dijkstra)： 把图中的顶点集合V分成两组。
第一组为已求出最短路径的顶点集合S(初始时S中只有源节点，以后每求得一条最短路径，就将它对应的顶点加入到集合S中，直到全部的顶点都加入到S中)；
第二组是未确定最短路径的顶点集合U；

【算法步骤】

1.初始化时，S只含有源节点；
2.从U中选取一个距离v最小的顶点k加入到S中(该距离就是v到k的最短路径长度)；
3.以k为新考虑的中间点，修改U中各顶点的距离；若从源节点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短，则修改顶点u的距离值，修改后的距离值是顶点k的距离加上k到u的距离。
4.重复步骤2和3.

2.弗洛伊德算法（Floyd）：

1，从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。
2，对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。