回溯算法（DFS）通用解题框架总结+实例分析

很少写这么长的总结，算法对上学期一个简单交代，就是时间花的漫长的，用了一下午。惩罚自己以后多写一点，不写不是中国人~嘻嘻?

什么是回溯算法？
回溯算法有“通用的解题法”之称。用它可以系统地搜索一个问题地所有解或任一解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。它在问题的解空间树中，按深度优先策略，从根节点出发搜索解空间树。算法搜索至解空间树的任一结点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先策略搜索。回溯法求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。回溯法求问题的一个解时，只要搜索到问题的一个解就可结束。这种以深度优先方式系统搜索问题解的算法称为回溯法，它适用于解组合数较大的问题。
回溯算法能解决哪些问题？
计数问题、优化问题、判定问题，通常能用搜索解决的问题都能用回溯算法。

回溯法的算法框架

●解空间树

●回溯基本思想

●约束与限界

●设计步骤

●代码框架

（1）解空间树

       用回溯法解问题时，应明确定义问题的解空间。问题的解空间至少应包含问题的一个（最优）解。子集数和排列树是用回溯法解题时常遇到的两类典型的解空间树。

当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间树称为子集树。

图为0-1背包问题的子集树，最后的解空间为{(1,1,1),(1,1,0),(1,0,1),(1,0,0),(0,1,1),(0,1,0),(0,0,1),(0,0,0)}

 

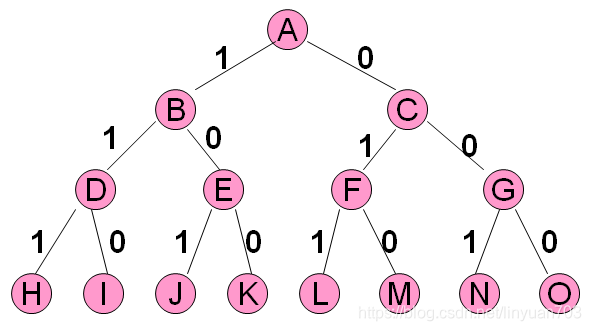
当所给的问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。

图为旅行商问题的排列树，最后的解空间为{(c1,c2,c3,c4),(c1,c2,c4,c3),(c1,c3,c2,c4),(c1,c3,c4,c2),(c1,c4,c2,c3),(c1,c4,c3,c2)}

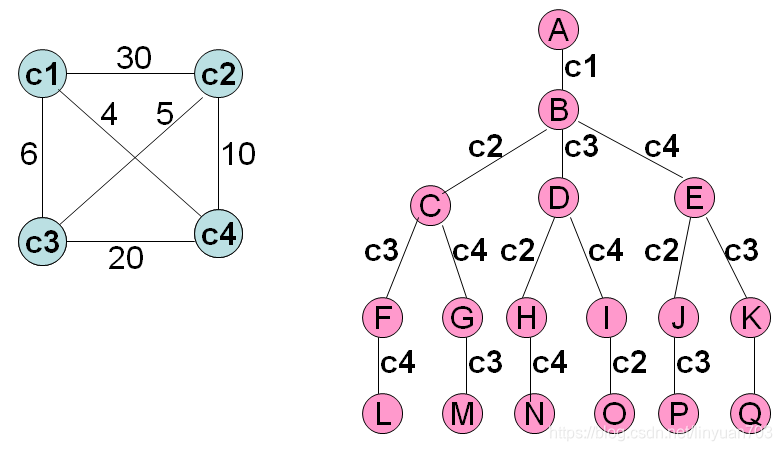
当然问题的解空间不止这两种，比如解决整数划分问题，单源最短路径问题，可以用路径树去定义它的解空间树。常见的解空间树如我上面介绍的两种，子集树和排列树。

（2）回溯基本思想

       确定了解空间的组织结构后，回溯法从开始结点(根结点)出发，以深度优先方式搜索整个解空间。这个开始结点成为活结点，同时也成为当前的扩展结点。在当前的扩展结点处,搜索向纵深方向移至个新结点。这个新结点就成为新的活结点，并成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向移动,则当前扩展结点就成为死结点。此时，应往回移动(回溯)至最近的一个活结点处，并使这个活结点成为当前的扩展结点。回溯法以这种工作方式递归地在解空间中搜索，直至找到所要求的解或解空间中已无活结点时为止。

       例如,对于n= 3时的0- 1背包问题,考虑下面的具体实例:w= [16,15,15],p= [45,25,25],c = 30。从图的根结点开始搜索其解空间.开始时,根结点是唯一的活结点,也是当前的扩展结点。在这个扩展结点处,可以沿纵深方向移至结点B或结点C。假设选择先移至结点B。此时,结点A和结点B是活结点，结点B成为当前扩展结点。由于选取了W1,故在结点B处剩余背包容量是r=14,获取的价值为45。从结点B处,可以移至结点D或E。由于移至结点D至少需要w2 = 15的背包容量,而现在仅有的背包容量是r=14,故移至结点D导致不可行解。搜索至结点E不需要背包容量,因而是可行的。从而选择移至结点E。此时,E成为新的扩展结点,结点A、B和E是活结点。在结点E处,r=14,获取的价值为45。从结点E处，可以向纵深移至结点J或K。移至结点J导致不可行解,而移向结点K是可行的，于是移向结点K,它成为新的扩展结点。由于结点K是叶结点,故得到个可行解。这个解相应的价值为45.x;的取值由根结点到叶结点K的路径唯一一 确定，即x= (1 ,0,0)。由于在结点K处已不能再向纵深扩展,所以结点K成为死结点。再返回到结点E处。此时在结点E处也没有可扩展的结点,它也成为死结点。

       接下来又返回到结点B处。结点B同样也成为死结点，从而结点A再次成为当前扩展结点。结点A还可继续扩展，从而到达结点C。此时，r=30，获取的价值为0。从结点C可移向结点F或G。假设移至结点F,它成为新的扩展结点。结点A,C和F是活结点。在结点F处，r=15，获取的价值为25。从结点F向纵深移至结点L处，此时，r = 0,获取的价值为50。由于L是叶结点，而且是迄今为止找到的获取价值最高的可行解，因此记录这个可行解。结点L不可扩展，我们又返回到结点F处。按此方式继续搜索，可搜索遍整个解空间。搜索结束后找到的最好解是相应0-1背包问题的最优解。

      下面再看一个用回溯法解旅行售货员问题的例子。

      旅行售货员问题的提法是:某售货员要到若千城市去推销商品，已知各城市之间的路程(或旅费)。他要选定一条从驻地出发 ，经过每个城市一遍，最后回到驻地的路线，使总的路程(或总旅费)最小。

      问题刚提出时 ,不少人都认为这个问题很简单。后来，人们在实践中才逐步认识到,这个问题只是叙述简单，易于为人们所理解，而其计算复杂性却是问题的输人规模的指数函数，属于相当难解的问题之一。事实 上,它是NP完全问题。这个问题可以用图论的语言形式描述。

      设G=(V,E)是一个带权图。图中各边的费用(权)为正数。图中的一条周游路线是包括V中的每个顶点在内的一条回路。周游路线的费用是这条路线上所有边的费用之和。旅行售货员问题要在图G中找出费用最小的周游路线。

      图是一个4顶点无向带权图,顶点序列c1,c2,c4,c3,c1;       c1,c3,c2,c4,c1       和c1,c4,c3,c2,c1是该图中3条不同的周游路线。

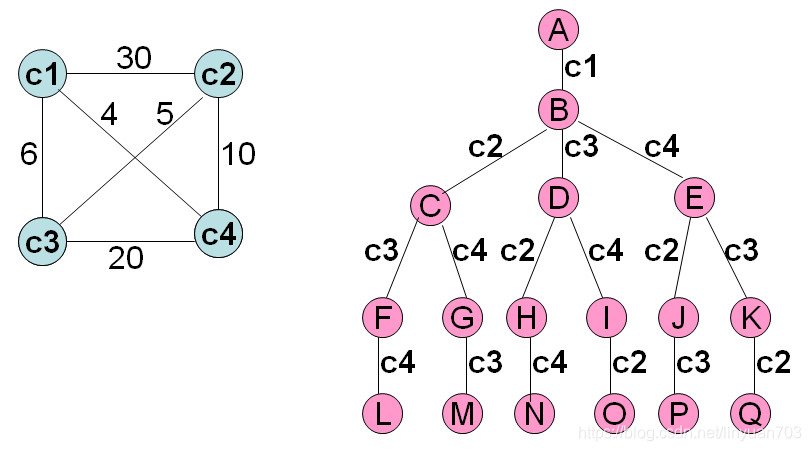
      旅行售货员问题的解空间可以组织成一棵树,从树的根结点到任一叶结点的路径定义了图G的一条周游路线。右图是当n= 4时解空间树