机器视觉3D算法现场应用讲解

B站  ：道传科技上位机   观看教程

一、工业自动化四个3D检测使用场景

‌尺寸与形状测量‌

包括平面度、表面角度、体积等特征，适用于复杂物体的高精度检测。 ‌

‌深度特征检测‌

测量物体表面的深度变化（如划痕、凹陷等），精度可达5-10微米，适用于微米级缺陷检测。 ‌

‌高度计算与体积计算‌

通过3D图像分析，可快速计算物体高度、体积等参数，用于自动化生产中的快速检测。 ‌

‌三维空间坐标定位‌

通过结构光、双目视觉等技术获取物体表面每一点的三维坐标，实现精准定位。

二、什么是3D相机和点云

3D相机不仅能够获得平面图像，还可以获得拍摄对象的深度信息，即三维位置及尺寸等。其原理主要依赖于结构光、双目视觉和光飞行时间法这三种技术。

在逆向工程中通过测量仪器得到的产品外观表面的点数据集合也称之为点云，通常使用三维坐标测量机所得到的点数量比较少，点与点的间距也比较大，叫稀疏点云；而使用三维激光扫描仪或照相式扫描仪得到的点云，点数量比较大并且比较密集，叫密集点云。

三、两种视觉方案

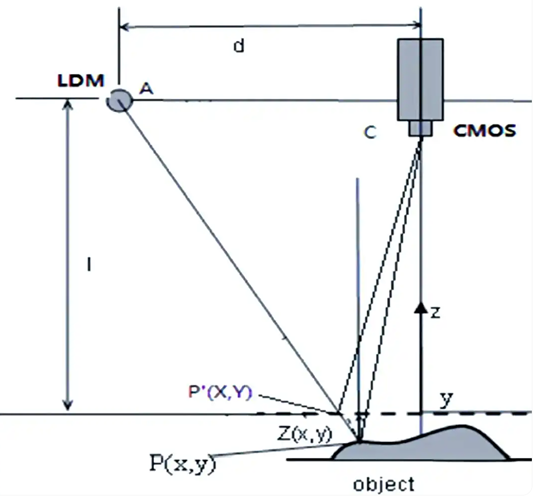
结构光，英文名为Structured light，其核心技术在于使用特定波长的红外激光作为光源，这种激光是不可见的。当这种激光经过特殊编码后，会投影到物体上。通过一系列算法，我们可以分析返回的编码图案的畸变情况，从而得出物体的精确位置和深度信息。    （距离越长精度越差）

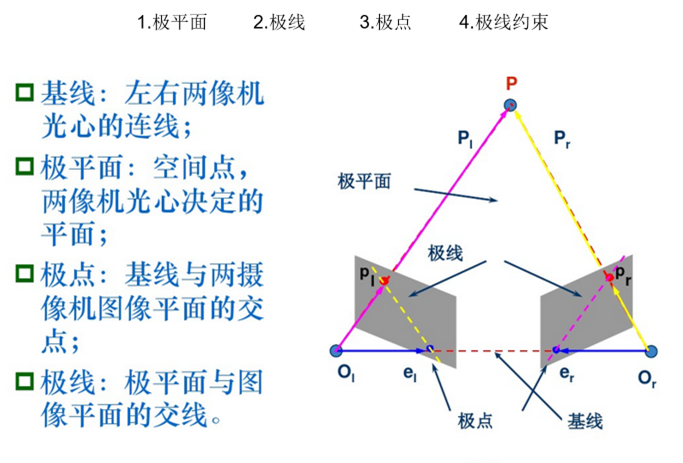
双目立体视觉是机器视觉的一种重要形式，基于视差原理，利用成像设备从不同的位置获取被测物体的两幅图像。通过计算图像对应点间的位置偏差，来获取物体三维几何信息。双目视觉有主动双目和被动双目之分，主动双目主动发射红外激光做补光，以便在夜晚也能使用。  （成本低，对光照要求极高）

四、流程讲解

（1、标定）

乒乓球，球心坐标的提取，可以针对点云分割后进行球心拟合，也可以通过模板匹配方式得到

求解R：基于平移组，获取乒乓球的球心XYZ，机器人多个姿态下的XYZ。使用点对直接求解RT，对应halcon中vector_to_hom_mat3d算子。此时Pose中的T是不对的

求解T：R已知，套公式求解              参考：文章（切记不要用内参标定，网上很多误导）

https://blog.youkuaiyun.com/weixin_42362219/article/details/142181787

五、模型调平

模型调平的目的：将模型调到和算子平面上，方便后续计算处理

下面方法是规则的模型

//计算最小包围盒在一个 3三维物体模型的点

smallest_bounding_box_object_model_3d (OriginObjectModel3D, 'oriented', boxPose, Length1, Length2, Length3)

//创建一个表示一个框的3维对象模型

gen_box_object_model_3d (boxPose, Length1, Length2, Length3, box)

// 显示模型

disp_object_model_3d (WindowHandle1, [OriginObjectModel3D,box], [], DispPose1, GenParamName, GenParamValue)

//模型反转  （使点云坐标轴与系统坐标系重合，便于后续处理）

pose_invert (boxPose, boxPoseInvert)

//将一个3维的构成转化为齐次变换矩阵

pose_to_hom_mat3d (boxPoseInvert, box_pose_HomMat3D)

//添加一个平移到齐次的3维变换矩阵。

hom_mat3d_translate (box_pose_HomMat3D, Length1/2, Length2/2, Length3/2, HomMat3DTranslate)

//应用任意仿射三维变换到三维物体模型。

affine_trans_object_model_3d (OriginObjectModel3D, HomMat3DTranslate, ObjectModel3DAffineTrans1)

//计算最小包围盒在一个 3三维物体模型的点。

smallest_bounding_box_object_model_3d (ObjectModel3DAffineTrans1, 'oriented', boxPose, Length1, Length2, Length3)

//创建一个表示一个框的3维对象模型

gen_box_object_model_3d (boxPose, Length1, Length2, Length3, box)

disp_object_model_3d (WindowHandle1,[ObjectModel3DAffineTrans1,box], [], DispPose2, GenParamName, GenParamValue)

六、获取平面

（一）

read_image (XYZ, '3d/3d_01.tif')

access_channel (XYZ, X, 1)

access_channel (XYZ, Y, 2)

access_channel (XYZ, Z, 3)

gen_ellipse (ROI_0, 84.5473, 95.7705, rad(-35.9506), 10.9232, 8.60448)

reduce_domain (Z, ROI_0, ImageReduced)

//从图像到一个3维对象模型的变换3个D点

xyz_to_object_model_3d (X, Y, ImageReduced, ObjectModel3D)

*直接使用halcon拟合平面算子处理

fit_primitives_object_model_3d (ObjectModel3D, 'primitive_type', 'plane', ObjectModel3DOut)

get_object_model_3d_params (ObjectModel3DOut, 'primitive_parameter', Result1)

get_object_model_3d_params (ObjectModel3DOut, 'primitive_rms', GenParamValue1)

*获取截取的3d模型x、y、z的坐标值

get_object_model_3d_params (ObjectModel3D, 'point_coord_x', pX)

get_object_model_3d_params (ObjectModel3D, 'point_coord_y', pY)

get_object_model_3d_params (ObjectModel3D, 'point_coord_z', pZ)

*求均值

XM:=mean(pX)   YM:=mean(pY)      ZM:=mean(pZ)

*去质心    DX:=pX-XM    DY:=pY-YM    DZ:=pZ-ZM

*求矩阵各个位置的值   MA11 := sum(DX * DX)    MA22 := sum(DY * DY)     MA33 := sum(DZ * DZ)

MA12 := sum(DX * DY)      MA13 := sum(DX * DZ)           MA23 := sum(DY * DZ)

create_matrix (3, 3, [MA11,MA12,MA13,MA12,MA22,MA23,MA13,MA23,MA33], MatrixID)

*实对称矩阵，求特征值和特征向量

eigenvalues_symmetric_matrix (MatrixID, 'true', EigenvaluesID, EigenvectorsID)

*特征值按小到大排列，所以平面法向量是第一列特征向量

get_value_matrix (EigenvectorsID, 0, 0, NX)

get_value_matrix (EigenvectorsID, 1, 0, NY)

get_value_matrix (EigenvectorsID, 2, 0, NZ)

*算C  平面方程NX*X+NY*Y+NZ*Z=C

C := NX * XM + NY * YM + NZ * ZM

Result2:=[NX,NY,NZ,C]

*对应使用直接求解法

*算矩阵各个位置的值

MB11:=sum(pX*pX)    MB12:=sum(pX*pY)    MB13:=sum(pX)     MB22:=sum(pY*pY)       MB23:=sum(pY)     MB33:=|pX|

MC1:=sum(pX*pZ)    MC2:=sum(pY*pZ)     MC3:=sum(pZ)

create_matrix (3, 3, [MB11,MB12,MB13,MB12,MB22,MB23,MB13,MB23,MB33], MB)

create_matrix (3, 1, [MC1,MC2,MC3], MC)

solve_matrix (MB, 'general', 0, MC, MatrixResultID)

get_full_matrix (MatrixResultID, Values)

*要求a^2+b^2+c^2=1 求解真正的a、c

dd:=Values[0]*Values[0]+Values[1]*Values[1]+1

a:=Values[0]/sqrt(dd)

b:=Values[1]/sqrt(dd)

c:=-1/sqrt(dd)

*因为这里的平面方程为a*x+b*y+c*z=d 与文章中方程A*x+B*y+C*z+D=0中d相差个负号，所以

d:=-Values[2]/sqrt(dd)

Result3:=[a,b,c,d]

*SVD分解法 

create_matrix (3, Num, [DX,DY,DZ], A)

transpose_matrix_mod (A)

svd_matrix (A, 'full', 'both', U, S, V)

get_full_matrix (V, VValues)

get_value_matrix (V, 0, 2, Value1)

get_value_matrix (V, 1, 2, Value2)

get_value_matrix (V, 2, 2, Value3)

Value4:=Value1*XM+Value2*YM+Value3*ZM

Result4:=[Value1,Value2,Value3,Value4]