二叉树遍历序列 与 区间划分递归

一、核心思想：根定位 + 左右划分，唯一确定二叉树

从遍历序列中，我们需要两类信息：

• 能定位根的位置：如前序首位为根、后序末位为根。
• 能切分左右子树的边界：如中序，根的左右部分分别是左子树与右子树；或利用二叉搜索树的大小关系（左全小于根，右全大于根）。

只有同时具备“根定位”和“左右划分”，才能唯一确定一棵二叉树。

---

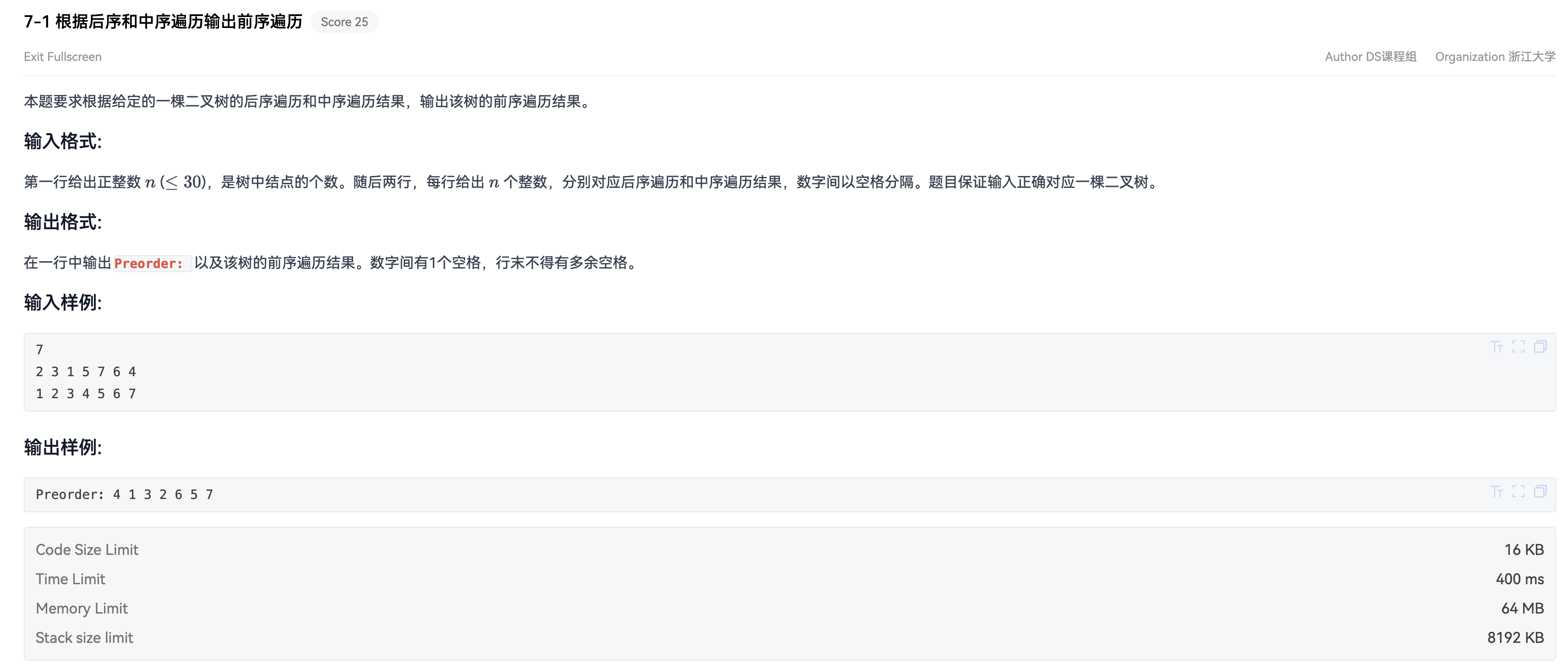
二、7-1 根据后序和中序遍历输出先序遍历

由后序 + 中序 → 输出前序

题意：给定后序与中序，输出该树的前序。
输入保证对应一棵合法二叉树，n ≤ 30。

递归思路

• 后序区间 [postL…postR] 的末位 post[postR] 是当前子树的根。
• 在中序 [inL…inR] 中找到根位置 i。则：
  • 左子树的中序区间为 [inL…i-1]。
  • 右子树的中序区间为 [i+1…inR]。
  • 左子树规模 k = i - inL。
• 用 k 在后序中切出左右子树：
  • 左后序：[postL…postL + k - 1]
  • 右后序：[postL + k…postR - 1]（注意根已占 postR）
• 根 -> 左子树 -> 右子树。

代码

#include <stdio.h>

int post[100], in[100];
int n;
int first = 0;

void dfs(int pl, int pr, int il, int ir)
{
    if(pl > pr || il > ir)return;

    int root = post[pr];
    if(first)printf(" %d", root);
    else printf("Preorder: %d", root);
    first = 1;

    int k = 0;
    for(int i = il; i <= ir; i ++)
        if(in[i] == root)
        {
            k = i;
            break;
        }
    int left = k - il;
    dfs(pl, pl + left - 1, il, k - 1);
    dfs(pl + left, pr - 1, k + 1, ir);
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)scanf("%d", &post[i]);
    for(int i = 1; i <= n; i++)scanf("%d", &in[i]);
    dfs(1, n, 1, n);
}

---

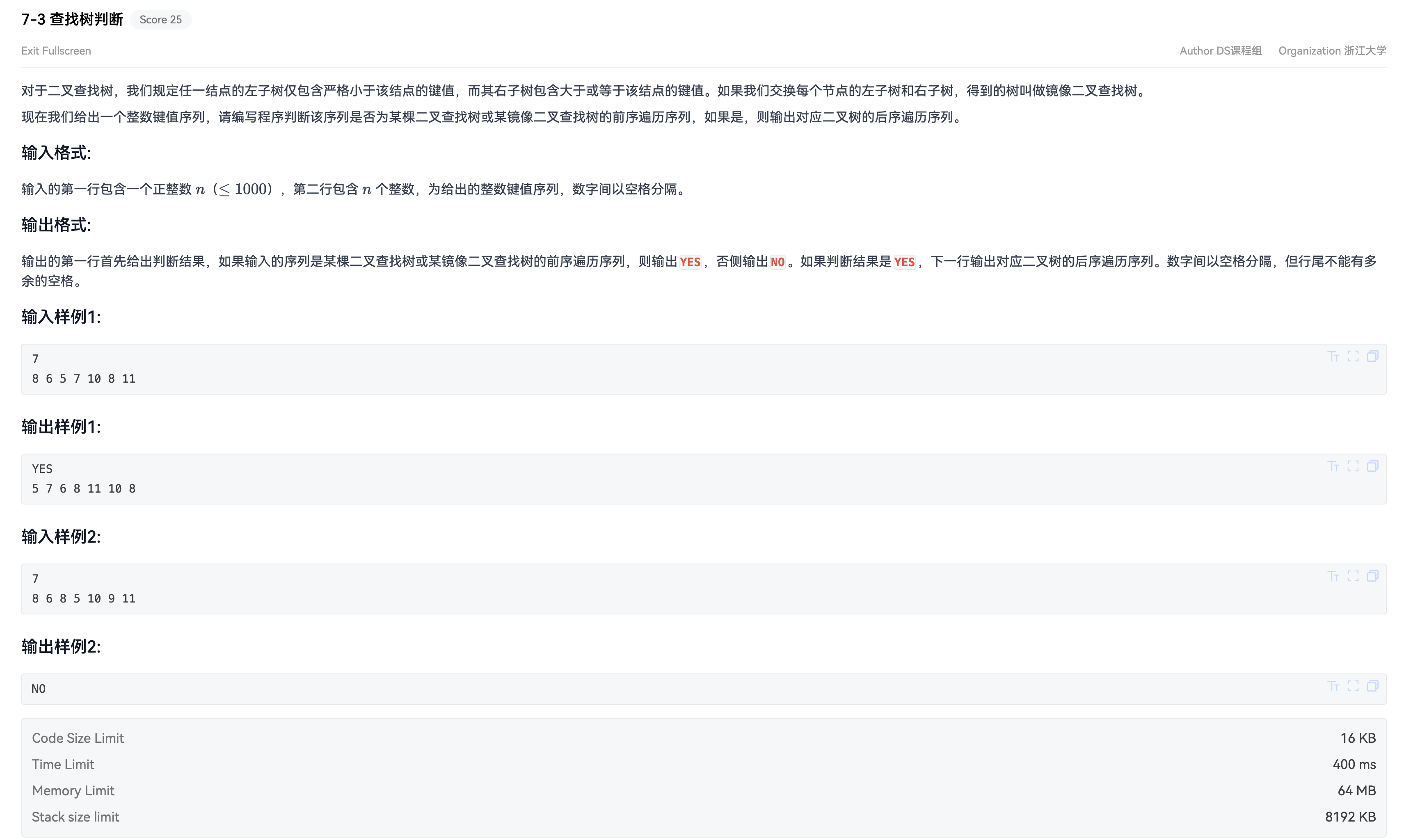
三、7-3 查找树判断

判断是否为 BST/镜像 BST 的前序，并输出后序

题意：给定一个序列，判断它是否可以作为某棵 BST 或镜像 BST 的前序；若是，输出对应的后序，否则输出 NO。
约定：BST 的右子树允许“≥ 根”（等于归右），镜像规则相反（左子树 ≥ 根，右子树 < 根）。

判定与构造（前序 + 规则 → 后序）

• 设当前区间 [L…R]，根为序列首位 pre[L]。
• BST 情况：
  • 从 L+1 开始，连续“小于根”的一段为左子树；遇到第一个“≥ 根”处即右子树开始。
  • 检查右段是否全部“≥ 根”，否则非法。
• 镜像 BST 情况：
  • 连续“≥ 根”的一段为左子树；遇到第一个“< 根”处即右子树开始。
  • 检查右段是否全部“< 根”，否则非法。
• 递归验证左右子树，若合法：左后序 -> 右后序 -> 根。

判定流程：

1. 先按假设为 BST 尝试构造与验证。
2. 若失败，再假设为镜像 BST 尝试。
3. 若两者都失败，输出 NO。

代码

#include <bits/stdc++.h>
using namespace std;

int pre[1010];
vector<int> post;

bool dfs(int l, int r, bool isMirror)
{
    if(l > r)return true;

    int root = pre[l];
    int split = l + 1;
    if(!isMirror)
    {
        while(split <= r && pre[split] < root)split ++;
        // split此时为右子树根节点
        for(int i = split; i <= r; i ++)
            if(pre[i] < root)return false;
    }
    else
    {
        while(split <= r && pre[split] >= root)split ++;
        // split此时为右子树根节点
        for(int i = split; i <= r; i ++)
            if(pre[i] >= root)return false;
    }

    // 判断子树是否合法
    if(!dfs(l + 1, split - 1, isMirror))return false;
    if(!dfs(split, r, isMirror))return false;
    post.push_back(root);
    return true;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;cin >> n;
    for (int i = 1; i <= n; i ++)cin >> pre[i];

    if(dfs(1, n, false))
    {
        cout << "YES" << '\n';
        for(int i = 0; i < (int)post.size(); i ++)
        {
            if(i)cout << ' ';
            cout << post[i];
        }
        return 0;
    }
    post.clear();
    if(dfs(1, n, true))
    {
        cout << "YES" << '\n';
        for(int i = 0; i < (int)post.size(); i ++)
        {
            if(i)cout << ' ';
            cout << post[i];
        }
        return 0;
    }
    cout << "NO\n";
    return 0;
}

原创