对于处理一些分类问题而并非预测问题,我们则需要使用logistic regression
对于分类问题的定义:parametric models to predict a discrete lable.
The lable / The result must be discrete!
1. 前提条件
需要重点强调的部分有,我们需要使用独热变量去定义任何一个lable,因为我们需要保证lable和lable之前的距离是相等的。独热变量的定义参见维基百科:
独热[1](英语:one-hot)在数字电路和机器学习中被用来表示一种特殊的比特组或向量,该字节或向量里仅容许其中一位为1,其他位都必须为0[2]。其被称为独热因为其中只能有一个1,若情况相反,只有一个0,其余为1,则称为独冷(one-cold)[3]。在统计学中,虚拟变量代表了类似的概念。
举个简单例子,如果定义猫是1,马是2,狗是3。就表示狗跟猫的距离是2,相当于说马比狗更接近猫的类别,这完全是错误的!所以正常情况应该用一个向量表示,如下图所示

所以说,使用逻辑回归需要有两个前提条件,一个是分类的类别需要预先定义好,一个是哪个独热变量代表哪个类别需要预先定义好。
2. 假设函数
同线性回归一样,逻辑回归也需要一个函数,可以是最简单的y = wx +b 也可以是高阶的多项式,这个取决于自己选择。但是不同的一点是,假设函数出来以后,我们需要把他带入到另一个函数中,叫Sigma函数。
函数图像如下图所示

这个函数的特点是无论x为多少,y值永远在1 和 0 之间浮动
所以最后我们的函数变为
3. 梯度下降
对于逻辑回归,我们使用的loss function 是
具体使用他的原因,是由概率论与数理统计中的最大似然估计(maximum likelihood estimation)得来的,最大似然估计的数学意义在于,算出当参数w确定是,发生这个事件y的概率。所以,需要保证最大似然估计值越大越好。最后经过一些数学运算,得出如上结果
至于我们为什么用这个误差函数而不用线性回归的那个误差函数,因为我们的sigma函数不是线性的,带入到上一个误差函数中会导致很多个局部最优解,无法完美的解决我们这个逻辑回归的问题
每次下降的幅度,和线性回归保持一致
最后经过复合函数的求导公式,得出如下结果
4. 逻辑回归得意义
逻辑回归的意义在于寻找决策边界,将不同类型的点分开
Logistic regression is to find a linear hyperplane to seperate the trainning data points
至于决策边界上的点,可以定义为正也可以定义为负,逻辑回归有个前提条件,datapoints 必须是linear separable如果data points 耦合的很紧密,不好找出分界线,则不适用逻辑回归
5. 多元逻辑回归
同0,1的逻辑回归一样,只不过我们不再用sigma function了,而用softmax function
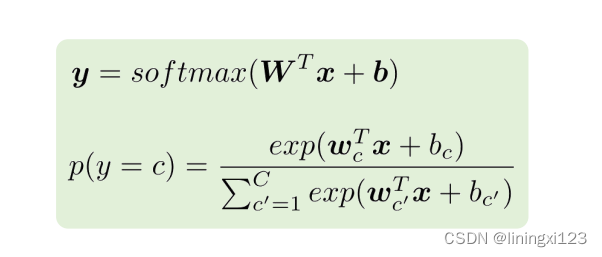




 本文详细介绍了逻辑回归的应用场景、前提条件及实现过程。首先探讨了独热变量的重要性,并解释了假设函数如何通过Sigmoid函数转换来预测离散标签。接着介绍了梯度下降法用于优化损失函数的过程,以及逻辑回归在寻找决策边界中的作用。
本文详细介绍了逻辑回归的应用场景、前提条件及实现过程。首先探讨了独热变量的重要性,并解释了假设函数如何通过Sigmoid函数转换来预测离散标签。接着介绍了梯度下降法用于优化损失函数的过程,以及逻辑回归在寻找决策边界中的作用。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








