2018 nowcoder 多校 4

最新推荐文章于 2025-07-28 16:12:12 发布

原创最新推荐文章于 2025-07-28 16:12:12 发布 · 188 阅读

0 ·

CC 4.0 BY-SA版权

2018多校题解专栏收录该内容

18 篇文章

订阅专栏

本文分享了几道编程竞赛题目，包括构造矩阵、花园美景评估、最大化众数等，并提供了详细的解题思路与代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

第四场了呀，每场都被教育到自闭……
补题进度：[6/10] 场上3

D Another Distinct Values：
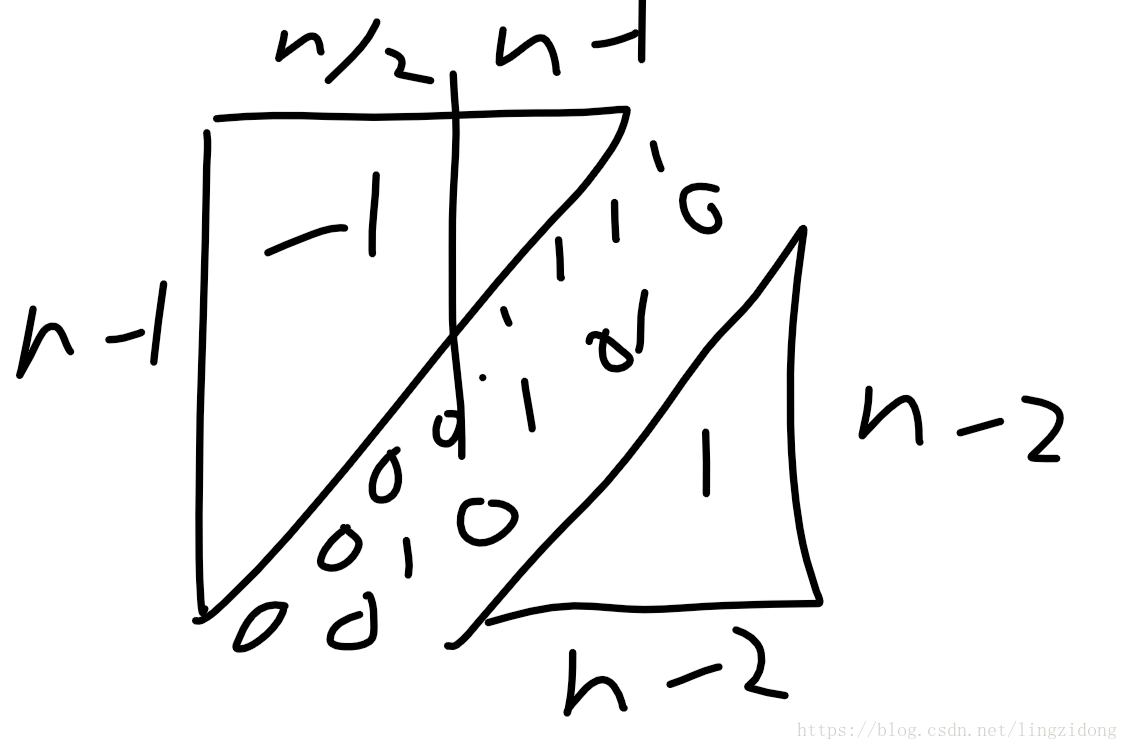
题意是构造一个NxN矩阵，矩阵中的元素都是-1，0，1组成。还要满足每一行，每一列得和均不相同的规则。
首先找规律，发现奇数得时候没有解，之后通过写暴力打表找到了一种规律，按照规律构造就行
这里写图片描述

#include <bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
#define fi first
#define se second
using namespace std;
const int maxn = 203;
int a[maxn][maxn];
int main()
{
    ios::sync_with_stdio(0);
    int ca;
    cin>>ca;
    while(ca--)
    {
        int n;
        cin>>n;
        if(n % 2) cout<<"impossible"<<endl;
        else
        {
            cout<<"possible"<<endl;
            for(int i = 1;i<=n;i++)
            {
               for(int j = 1;j<=n;j++)
               {
                    if(i + j <= n)
                    {
                        a[i][j] = -1;
                    }
                    else if(i + j > n +2)
                    {
                        a[i][j] = 1;
                    }
                    else if(i + j == n + 1)
                    {
                        //cout<<j<<endl;
                        if(j <= n/2) a[i][j] = 1;
                        else a[i][j] = -1;
                    }
                    else
                    {
                        if(j % 2) a[i][j] = 1;
                        else a[i][j] = 0;
                    }


               }
            }
            for(int i = 1;i<=n;i++)
            {
                for(int j = 1;j<=n;j++)
                {
                    cout<<a[i][j]<<' ';
                }
                cout<<endl;
            }

        }
    }
    return 0;
}

F Beautiful Garden
看数据量这道题直接模拟就行了，但是我想了一个比较麻烦的做法……
首先记录下(0,n),(1,n-1),…,(n/2-1,n/2+1)，从第一行和最后一行开始中间有几个连续的相等的对，记为p，对于列也做这样的处理，记为q
然后如果p == n/2的时候，因为中轴线线上不能当成宽度，就p–，q以此类推，答案就是p*q

#include <bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
#define fi first
#define se second
using namespace std;
const int maxn = 2003 ;
char g[maxn][maxn];
int main()
{

    int ca;
    cin>>ca;
    int n,m;
    while(ca--)
    {
        scanf("%d%d", &n,&m);
        int p = 0,q = 0;
        for(int i = 0;i<n;i++)
        {
            scanf("%s", g[i]);
        }
        for(int i = 0;i<n/2;i++)
        {
            int f = 0;
            for(int j = 0;j<m;j++)
            {
                if(g[i][j] != g[n - i -1][j])
                {
                    f = 1;break;
                }
            }
            if(f) break;
            else p++;
        }
        for(int j = 0;j<m/2;j++)
        {
            int f = 0;
            for(int i = 0;i<n;i++)
            {
                if(g[i][j] != g[i][m - j -1])
                {
                    f = 1;break;
                }
            }
            if(f) break;
            else q++;
        }
        if(n == 2 || m == 2 || p == 0 || q == 0) cout<<0<<endl;
        else if(p == 1 || q == 1)
        {
            cout<<p*q<<endl;
        }
        else
        {
            if(p == n/2)p--;
            if(q == m/2)q--;
            cout<<p*q<<endl;
        }
    }
    return 0;
}

G Maximum Mode
这道题题意就是从n个数中删除m个数，让最后的众数最大。
枚举下答案，判断能不能借由删除m个数让其称为众数。

#include <bits/stdc++.h>
#include<cstring>
using namespace std;
#define ll long long
#define INF 1000000007
    set<int> _set;
map<int,int> _map;
    set<int>::iterator its;
    map<int,int>::iterator itm;
int n,m;
bool pd(int x)
{
    ll ans(0);
    bool flag(0);
    for(itm=_map.begin();itm!=_map.end();itm++)
    {
        if(itm->second==x )
            if(flag==0)
        {
                flag=1;
        }
        else
            ans+=1;
        if(itm->second >x)
            ans+=itm->second -x+1;

    }
    if(ans>m)return 0;
    return 1;
}
int main()
{
  //  freopen("input.txt","r",stdin);
    int T,maxx;
    ll x;
    cin>>T;
    while(T--)
    {
        cin>>n>>m;
        _set.clear();
        _map.clear();
        maxx=0;
        for(int i=0;i<n;i++)
        {
            cin>>x;
            _set.insert(x);
            _map[x]++;
            maxx=max(maxx,_map[x]);
        }
//        vector<int> v;
//        for(it=_set.begin();it!=_set.end();it++)
//        {
//            v.push_back(v[*it]);
//        }
//        sort(v.begin(),v.end();greater<int>());
        int l=1,r=maxx;
        while(l<=r)
        {
           // cout<<l<<' '<<r<<endl;
            int mid=(l+r)>>1;
            if(pd(mid))
                r=mid-1;
            else l=mid+1;

        }

       // cout<<l<<endl;
        int ans=0;
        for(its=_set.begin();its!=_set.end();its++)
            if(_map[*its]>=l)
                ans=max(ans,*its);
        if(ans==0)ans=-1;
        cout<<ans<<"\n";
    }
    return 0;
}

J Hash Function
题意是给出一个hash的结果，求一开始的插入序列。
场上想出来可能是拓扑排序，但是没敢写……
从hash表⾥里里能得出的信息：一个区间里里面的数要比一个数插入的早，也就是，利用这个信息我们可以减少一点边数
我学习了dls（%%%%%%）的解法，用并查集判断当前的点的下一个是不是先来的，如果不是的话就吧这条边添加进去

#include <bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
#define fi first
#define se second
#define pr pair<int,int>
#define mp make_pair
using namespace std;
const int maxn = 2e5 + 5;
int f[maxn],h[maxn],vis[maxn];
int n;
vector<int> ans;
set<pr> q;
int Find(int x)
{
    return f[x] == x ? x : f[x] = Find(f[x]);
}

void topo()
{
    ans.clear();
    q.clear();
    for(int i = 0;i<n;i++)
    {
        if(vis[i] == 0 && h[i] % n == i)
        {
            vis[i] = 1;
            q.insert(mp(h[i],i));
        }
    }
    while(!q.empty())
    {
        pr c = *q.begin();
        q.erase(q.begin());

        ans.push_back(c.fi);
        f[c.se] = Find((c.se+1) % n);
        if(Find(c.se) != c.se)
        {
            int v = Find(c.se);
            if(vis[v] == 0 && Find(h[v]%n) == v)
            {
                vis[v] = 1;
                q.insert(mp(h[v],v));
            }
        }
    }
}
int main()
{
    //ios::sync_with_stdio(0);
    int ca;
    cin>>ca;
    while(ca--)
    {
        cin>>n;
        for(int i = 0;i<n;i++)
        {
            cin>>h[i];
            vis[i] = 0;
            if(h[i] == -1) vis[i] = 1;
        }
        for(int i = 0;i<n;i++)
        {
            f[i] = i;
        }

        topo();
        int flag = 1;
        for(int i = 0;i<n;i++)
        {
            if(vis[i] == 0) flag = 0;
        }
        if(flag)
        {
            //cout<<ans.size()<<endl;
            for(int i = 0;i<ans.size();i++)
            {
                if(i != 0) cout<<' ';
                cout<<ans[i];
            }
            cout<<endl;
        }
        else
        {
            cout<<-1<<'\n';
        }
    }
    return 0;
}

A Ternary String
题意是按照一个规则添加字符每一时间删除开头一个字符，问一个串最后需要多长时间来消失。
设当前位置之前花费了 x 时间，那么：
对于当前字符为0，就是 x+1
对于当前字符1，之前已经产生了 x 个 0，那么将 1 的影响全部消除需要 x+2 次操作。
对于当前字符2，通过一波计算可以发现需要 $3*(2^{x+1}-1)$ 次操作
但是还有个点，由于 x 可能很大，需来一波欧拉降幂，首先预处理出来每个幂降幂用的phi，然后带入计算就行

#include <iostream>
#include <cstring>
#include <queue>
#include <cstdio>
#include <algorithm>
#include <set>
#include <unordered_map>
#include <map>
using namespace std;
#define ll long long
const int maxbit = 64;
const int mod = 1e9+7;
const int offset = 65;

int dp[maxbit][offset*2][2];
bool vis[maxbit][offset*2][2];
bool bit[maxbit];
int dfs(int pos,int sum,bool mask,bool limit)
{
    if(pos == -1) return abs(sum-offset);
    if(!limit)
    {
        if(vis[pos][sum][mask]) return dp[pos][sum][mask];
        vis[pos][sum][mask] = 1;

        int &ref = dp[pos][sum][mask];
        ref = (ref + dfs(pos-1,sum + (mask == 0 ? 1 : -1),0,0)) % mod;
        if(!limit || (limit && bit[pos]))
            ref = (ref + dfs(pos-1,sum+(mask == 1 ? 1 : -1),1,0)) % mod;
        return ref;
    }
    int res = dfs(pos-1,sum + (bit[pos] == mask? 1 : -1),bit[pos],1) % mod;
    if(bit[pos]) res = (res + dfs(pos-1,sum + (mask == 0 ? 1 : -1),0,0))% mod;
    return res;
}
void solve(ll n)
{
    for(int i = 0;i < maxbit;i++)
    {
        bit[i] = n & ( 1LL<< i);
    }
    for(int i =maxbit-1;i >= 0;i--)
    {
        if(bit[i])
        {
            int ans = dfs(i-1,offset,1,1);
            for(int j= i -1;j >= 0;j--)
            {
                ans  = (ans + dfs(j-1,offset,1,0)) % mod;
            }
            printf("%d\n",ans);
            return ;
        }
    }
    printf("0\n");
    return ;
}
int main()
{
    int ca;
    scanf("%d",&ca);
    while(ca--)
    {
        ll n;
        scanf("%lld",&n);
        solve(n);
    }
    return 0;
}

C Chiaki Sequence Reloaded
通过分析了数列的差分，我还是没有想出来a[n]是n二进制表示下相邻位置不同的个数和相邻位置相同的差。后来发现差分的是二进制相差一位的数，于是强行套上去了。
然后我们就可以愉快的数位dp了，dp[i][j][k] 表示前i位，当前相同和是j，然后这一位是1/0的和，找到最高位的1然后计算一下（前）后缀和。

#include <iostream>
#include <cstring>
#include <queue>
#include <cstdio>
#include <algorithm>
#include <set>
#include <unordered_map>
#include <map>
using namespace std;
#define ll long long
const int maxbit = 64;
const int mod = 1e9+7;
const int offset = 65;

int dp[maxbit][offset*2][2];
bool vis[maxbit][offset*2][2];
bool bit[maxbit];
int dfs(int pos,int sum,bool mask,bool limit)
{
    if(pos == -1) return abs(sum-offset);
    if(!limit)
    {
        if(vis[pos][sum][mask]) return dp[pos][sum][mask];
        vis[pos][sum][mask] = 1;

        int &ref = dp[pos][sum][mask];
        ref = (ref + dfs(pos-1,sum + (mask == 0 ? 1 : -1),0,0)) % mod;
        ref = (ref + dfs(pos-1,sum+(mask == 1 ? 1 : -1),1,0)) % mod;
        return ref;
    }
    int res = dfs(pos-1,sum + (bit[pos] == mask? 1 : -1),bit[pos],1) % mod;
    if(bit[pos]) res = (res + dfs(pos-1,sum + (mask == 0 ? 1 : -1),0,0))% mod;
    return res;
}
void solve(ll n)
{
    for(int i = 0;i < maxbit;i++)
    {
        bit[i] = n & ( 1LL<< i);
    }
    for(int i =maxbit-1;i >= 0;i--)
    {
        if(bit[i])
        {
            int ans = dfs(i-1,offset,1,1);
            for(int j= i -1;j >= 0;j--)
            {
                ans  = (ans + dfs(j-1,offset,1,0)) % mod;
            }
            printf("%d\n",ans);
            return ;
        }
    }
    printf("0\n");
    return ;
}
int main()
{
    int ca;
    scanf("%d",&ca);
    while(ca--)
    {
        ll n;
        scanf("%lld",&n);
        solve(n);
    }
    return 0;
}