C语言函数递归详解

算法沉淀归沉淀，知识部分也不能落下，这篇我们主要讲函数的递归这部分的知识点，全篇从理解再到使用递归再到使用函数递归隐患及为什么会有这个隐患，至于最后面的那个部分因为讲解起来也会花很多时间，所以这边虽然会讲但不会讲的很细致，之后会写一篇关于函数栈帧的创建与销毁的博客来具体讲一讲这一块的问题。

那么，话不多说，我们进入正文——————>

1.递归基础

函数的递归是不管学习哪一门计算机语言都会接触到的一个东西，那递归到底是个什么东西呢，我们先从这个讲起

1.1 什么是递归

先前我们在C语言数组和函数详解（https://blog.youkuaiyun.com/lingran__/article/details/151071631）这篇文章里讲过了函数调用是什么

而函数的递归就是在一个函数里面调用了这个函数，而不是调用别的函数（简称自己调用自己），这就是函数的递归

一般递归都是调用自定义函数，但其实主函数也是可以递归的，主函数的递归具体代码如下，这也是史上最简单的C语言函数递归代码

#include <stdio.h>
int main()
{
 printf("hehe\n");
 main();//main函数中⼜调⽤了main函数 
 return 0;
}

上面只是个举例，代表主函数可以递归，但是主函数递归是明显错误的，因为主函数如果递归了，如果能让程序走到调用函数那块，那就会无限调用下去了，最终代码就会陷入死循环了，循环着循环着，随着函数的不断调用，不断的开辟新空间，最终就会导致栈溢出（Stack overflow）

所以上面的代码如果实在VS运行时候，他会爆出未经处理异常的标志（即红叉叉），问题就是这个程序会导致栈溢出，如图

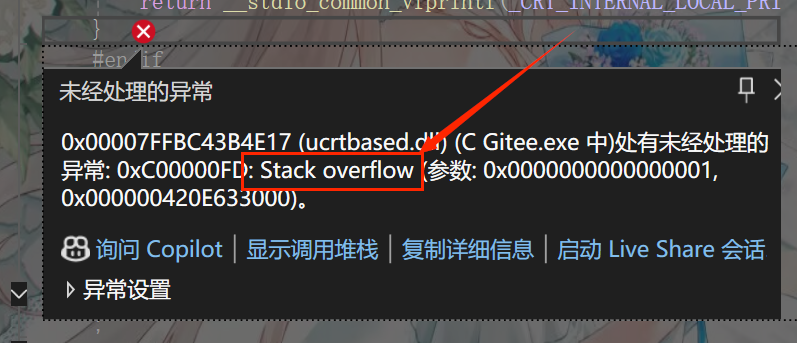
这个提示便是栈溢出

1.2 递归的思想

当遇到一个很大的问题的时候，可以将这个很大的问题转换为一个个与原先的问题相似的子问题来解决，当所有子问题都无法再拆分的时候，递归就完成了，把子问题全部解决完，主问题也自然就迎刃而解了。

所以递归的思想便是将大事化小的过程

那么，为什么叫递归呢

递是递推的意思，相当于把大问题拆成子问题的过程

归便是回归的意思，相当于是把子问题解决完的东西返回给子问题的主问题的过程

那么，我将会在递归举例的部分让你们慢慢体会这俩个过程

1.3 递归的限制条件

在用函数的递归的时候，需要满足以下俩个必要条件

1.递归存在限制条件，如果达到了这个限制条件，就结束递归

2.每次递归都会接近限制条件

我会在下面递归举例环节，让你们慢慢体会这俩个必要条件

2.递归举例

2.1 求ｎ的阶乘

2.1.1 题目要求：

输入一个数ｎ，输出ｎ的阶乘

2.1.2 分析与代码实现

这题如果不用递归打的话就直接一个for循环结束了（这便是迭代）

那么，如果用递归打的话怎么打呢

首先我们先把一个大的问题拆成子问题来看

那么，这个式子就很符合了 ｎ！＝ｎ＊（ｎ－１）！

当ｎ＝０时，阶乘为１，其余情况都可以用上面式子表示，那么就是下图

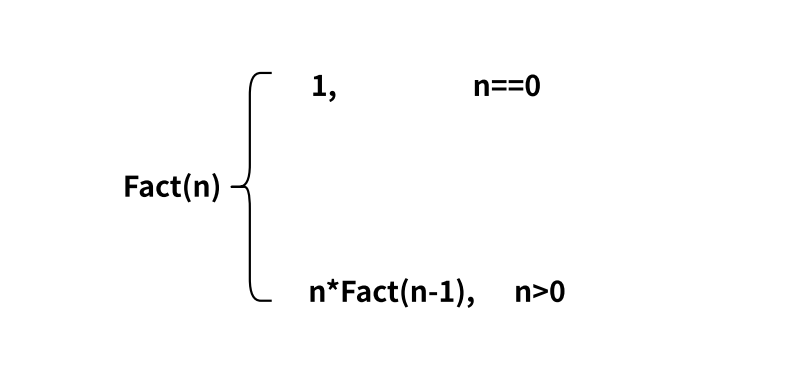那我们就可以写出函数Fact求n的阶乘，假设Fact(n)就是求n的阶乘，那么Fact(n-1)就是求n-1的阶乘

那我们就可以写出这个函数来实现这个功能了，如下

int Fact(int n)
{
 if(n==0)
 return 1;
 else
 return n*Fact(n-1);
}

那么，主体代码写完了，那整体的代码实现自然就不难了，如下

#include <stdio.h>
int Fact(int n)
{
 if(n==0)
 return 1;
 else
 return n*Fact(n-1);
}
int main()
{
 int n = 0;
 scanf("%d", &n);
 int ret = Fact(n);
 printf("%d\n", ret);
 return 0;
}

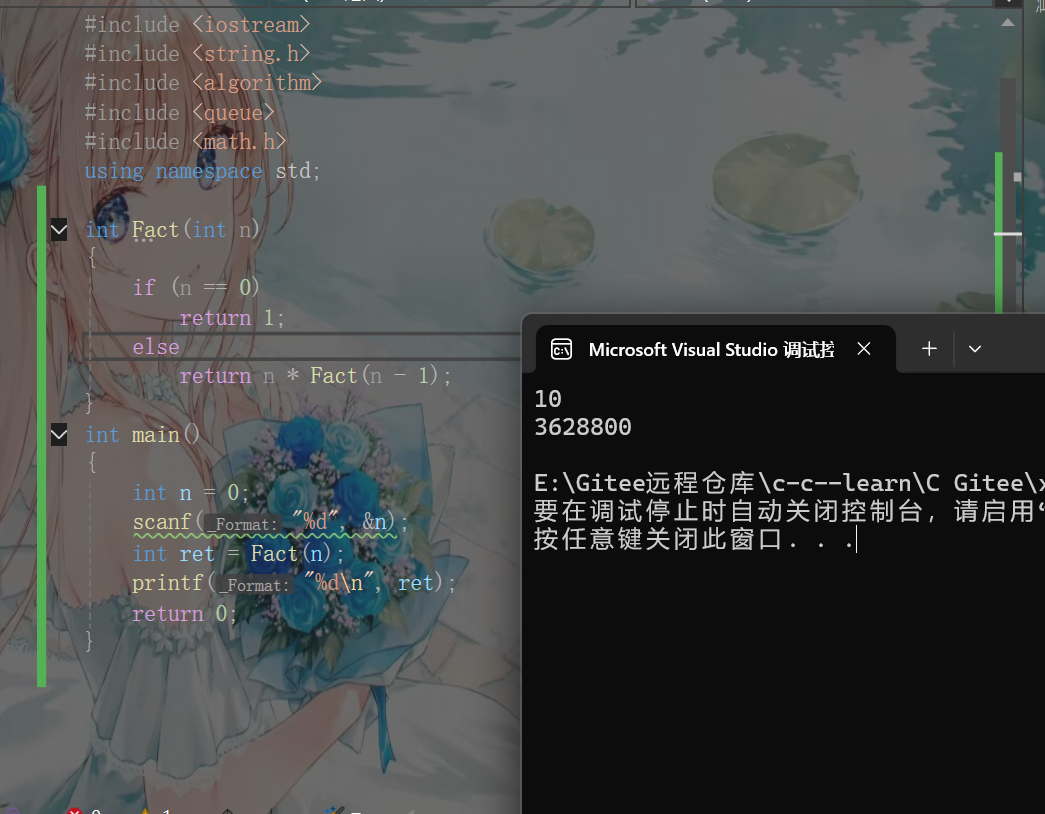
运行结果如图（这里输入的数不能太大，因为会超出数据范围存储范围，如果要输很大的数就要用到高精度了，这不在这篇讲的范畴，有兴趣的可以自己去了解下哦）

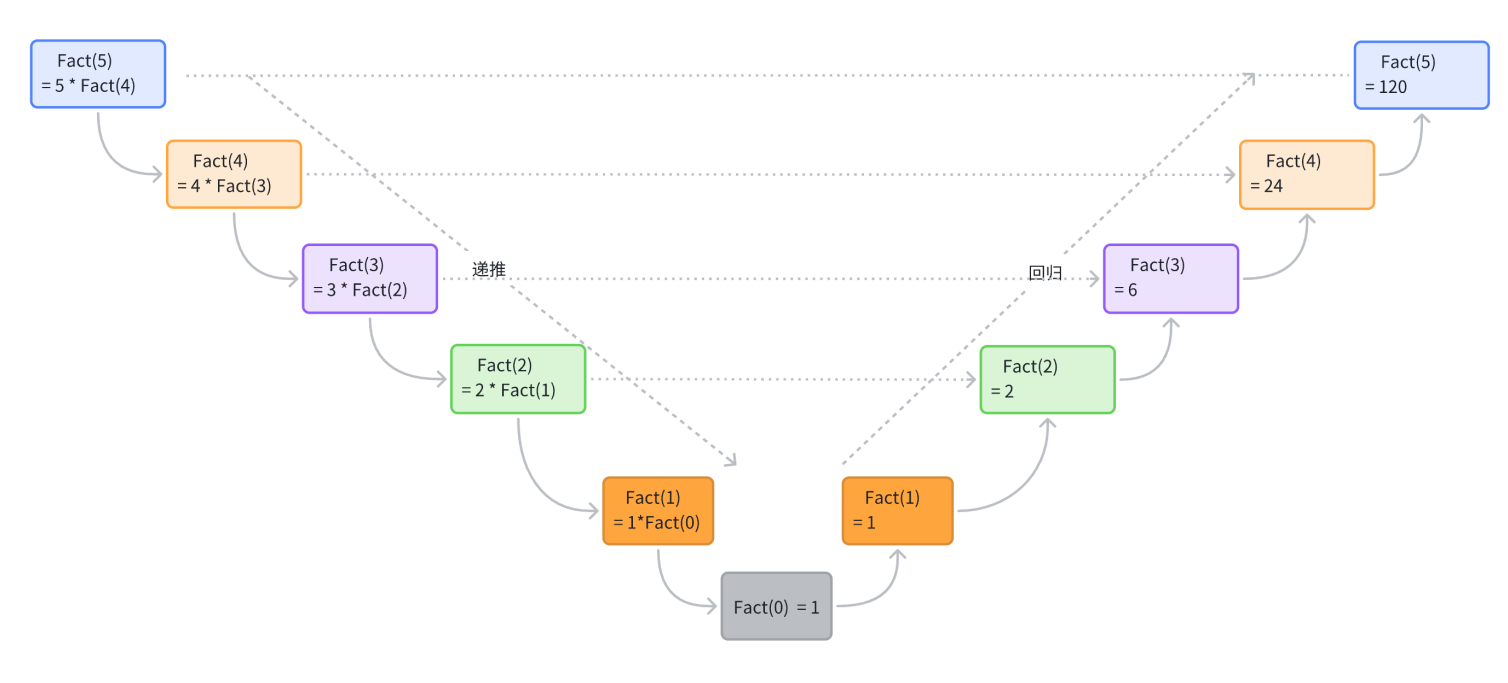
2.1.3 画图解析

上面那个递归的过程通过图来表示的话就是这个样子，正符合了递归的递推和回归

2.2 顺序打印一个整数的每一位

2.2.1 题目要求

输入一个整数ｍ，按照顺序打印整数的每一位

比如：

输入：1234 输出：１２３４

2.2.2 分析与代码实现

如果想要的到一个数的每一位，很简单，就是％１０然后再／１０就好啦，伪代码如下

while(n)
{
    printf("%d",n%10);
    n /= 10;
}

但是如果是这么写的话，输出的位就是倒着输出了

但是我们通过这个代码，我们可以知道数的最低位是最容易得到的，只需要%10就可以得到了，那么，我们就可以用递归来实现先取模到底再打印，我们结合代码来分析

void Print(int n)
{
 if(n>9)
 {
 Print(n/10);
 }
 printf("%d ", n%10);
}
int main()
{
 int m = 0;
 scanf("%d", &m);
 Print(n);
 return 0;
}

首先，当ｎ大于９的时候，就代表当前ｎ不是一位数，就一直递归，直到ｎ为个位数时，输出这个值，然后这个函数就结束了，返回上一个的函数，接着往下走，那上一个函数ｎ是２位，输出的取模１０就自然是高到低的第二位数了，然后这个函数也走完了，继续返回上一个函数，那上一个函数就是３位数了，取模１０输出的就是第三位数了，依次往后也是如此

为了加深理解，接下来我们就进入图的解析环节

2.2.3 画图解析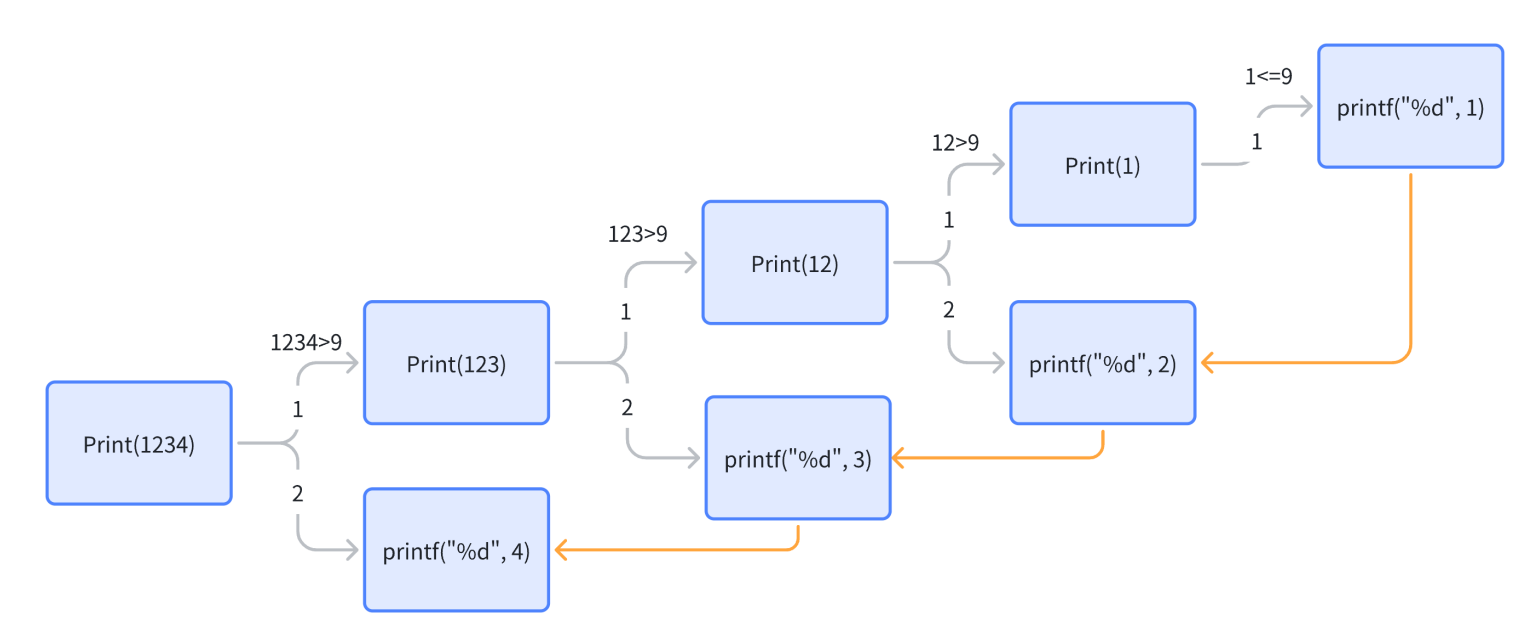

3.递归与迭代

接下来，我们来讲一下递归与迭代，递归会经常调用函数，导致会一直向栈区申请空间，直到这个函数结束才会释放空间，如果递归的深度很深的话就很容易导致栈溢出

这时候，迭代就出来了，就比如２.１的那个题目，直接ｆｏｒ循环乘下去效率肯定是比递归高的，这便是迭代的好处，他不需要时不时申请，释放空间，没有栈溢出的担忧

我们也能举出更加极端的例子，就像计算第n个斐波那契数，是不适合使用递归求解的，但是斐波那契数的问题通过是使用递归的形式描述的，如下：

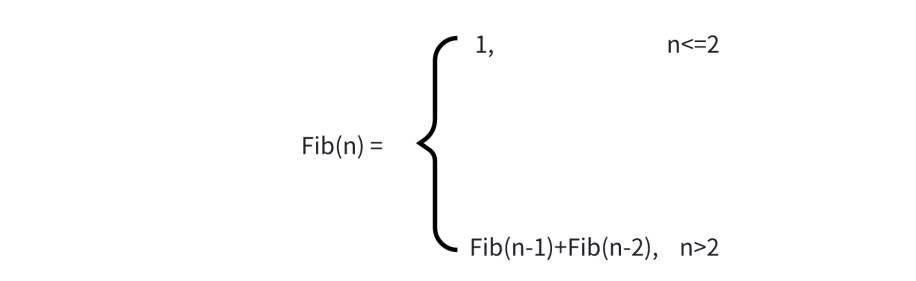
看到这个公式，很容易就诱导到递归去了，但递归你会发现数一大，就栈溢出来，计算所花费的时间也是很多的，十分的低效，为什么呢，我们一看图便知

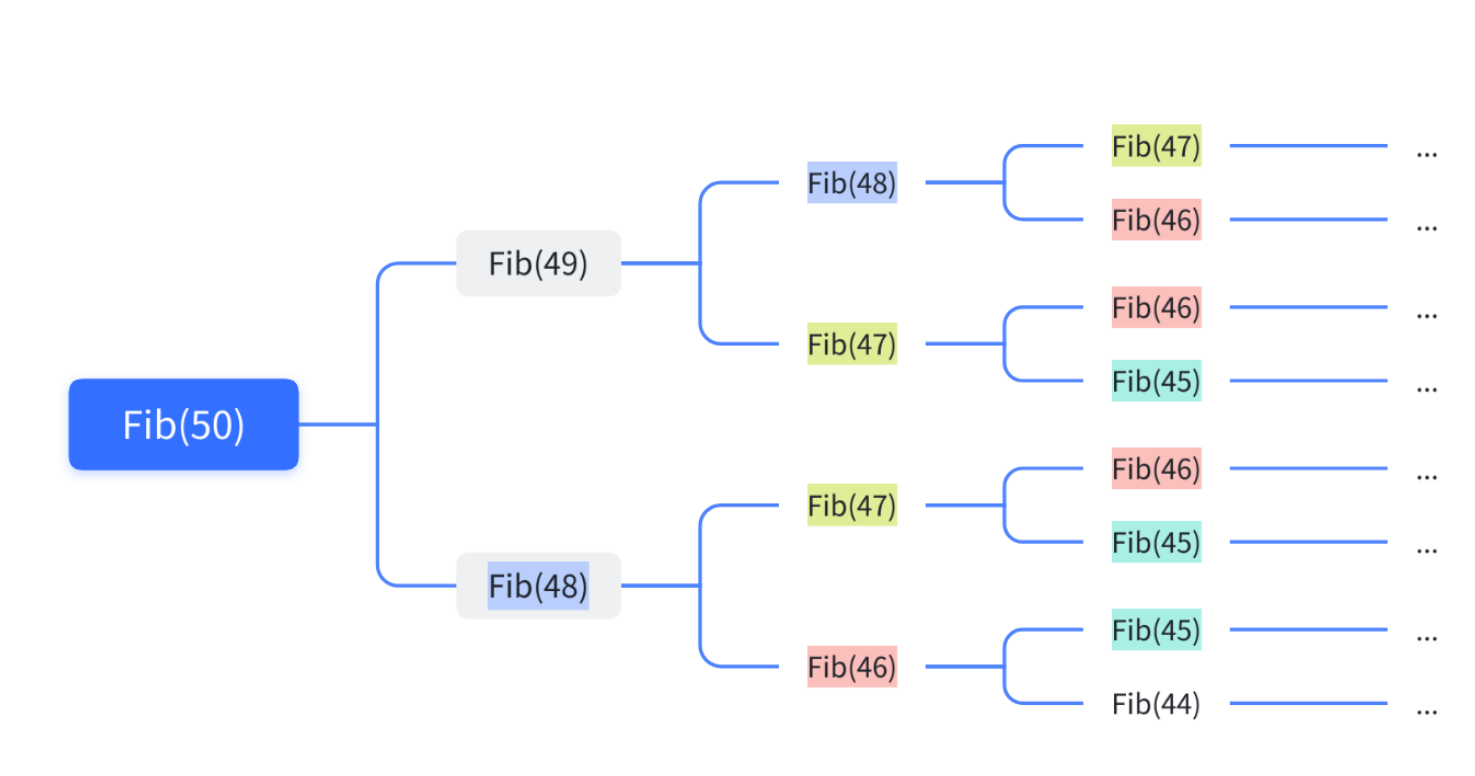
随着递归程序的不断展开，在展开的过程中，我们很容易就能发现，在递归的过程中会有重复计算，而且递归层次越深，冗余计算就会越多（可以用记忆化搜索优化，这样也没问题，但这个算算法了，就不在这讲啦，有兴趣的可以自己去搜一下哦）

所以在这种时候，我们就可以把这个递归优化成迭代的方式来实现

我们知道斐波那契数的前2个数都1，然后前2个数相加就是第3个数，那么我们从前往后，从小到大计算就行了。

这样，就有了下面的代码

int Fib(int n)
{
 int a = 1;
 int b = 1;
 int c = 1;
 while(n>2)
 {
 c = a+b;
 a = b;
 b = c;
 n--;
 }
 return c;
}

用迭代的方式来实现代码，效果就会比递归好很多了

结语：

那么，函数递归部分的讲解就讲解完啦，虽然内容不多，但是还是挺重要的，要尝试去用递归来解决问题，如果能优化递归也可以尝试优化成迭代的方式来表述

希望内容对你们有帮助，觉得好的话可以分享给朋友哟，毕竟虽然一个人走的快，但一群人走的远，谢谢观看啦