速通ACM省铜第二十天赋源码（HNCPC2022 Big Matrix 和 Fibonacci Cane）-优快云博客

引言：

今天是速通ACM的最后一期啦，刚好训练了整数天，goooood，最后一天，也是打了一次模拟赛，感觉拿铜有点玄乎啊，但问题不大，我们先来看一下这场模拟赛我打出来的俩道题，还有一道题我感觉没问题，但我蒸了一小时还没蒸出来有什么问题，所以放弃了，最终只开出俩道

最终战果

那么接下来，就进入今天的题目讲解啦——————————————>

Fibonacci Cane

我们先来看俩题中比较简单的一道题

题意分析

这里就直接放题目了，题目如图

因为是模拟赛，就没有用翻译插件了，这题的题目意思其实很简单，就是有一个斐波纳契数列，然后从这个数列中截取一个连续的子数列，是否存在一段子数列可以等于输入的值，若不存在符合条件的子数列，则输出NO

题目其实就这么简单，那么，接下来我们就进入逻辑梳理环节

逻辑梳理

这道题其实只需要知道一个细节就可以了，那就是斐波纳契的进位速度是很快的，虽然数据范围给了10的15次，但是除开第一位的斐波纳契会有比较多个，后面几位的斐波纳契基本都只有5，6个，所以只需要一个100的long long数组就可以装下所有条件范围内的斐波纳契数了

那么，斐波纳契数的存储已经存完了，那么假设有100个数，而且这100个数都是10的15次的大小，那么加起来最多也就只有10的17次，也没有超出 long long 的上限，所以我们就可以用前缀和来运算所有的情况，只要存在就输出YES，不存在就输出NO即可

这题的逻辑还是很简单的，那么接下来我们就进入代码实现的环节

代码实现

这边就直接放AC码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
long long a[100];
long long sum[100];
queue <long long>q;
int main()
{
    long long x = 1;
    long long y = 1;
    long long c = 1;
    while (1)
    {
        if (c <= 1000000000000000)
            q.push(c);
        else
            break;
        c = x + y;
        x = y;
        y = c;
    }
    int i = 1;
    int n = 1;
    while (!q.empty())
    {
        a[i] = q.front();
        sum[i] = sum[i - 1] + a[i];
        q.pop();
        n = i;
        i++;
    }
    long long k;
    while (cin >> k)
    {
        int xixi = 0;
        for (i = 1; i <= n; i++)
        {
            if (a[i] == k)
            {
                xixi = 1;
                break;
            }
        }
        for (i = 1; i < n; i++)
        {
            for (int j = i + 1; j <= n; j++)
            {
                if (sum[j] - sum[i - 1] == k)
                {
                    xixi = 1;
                    break;
                }
            }
            if (xixi)
                break;
        }
        if (xixi)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}

Big Matrix

然后就是剩下的一道开出的题了，这题涉及到了线性代数中矩阵的知识点，那么我们先来看题目

题意分析

依旧是直接放题目啦

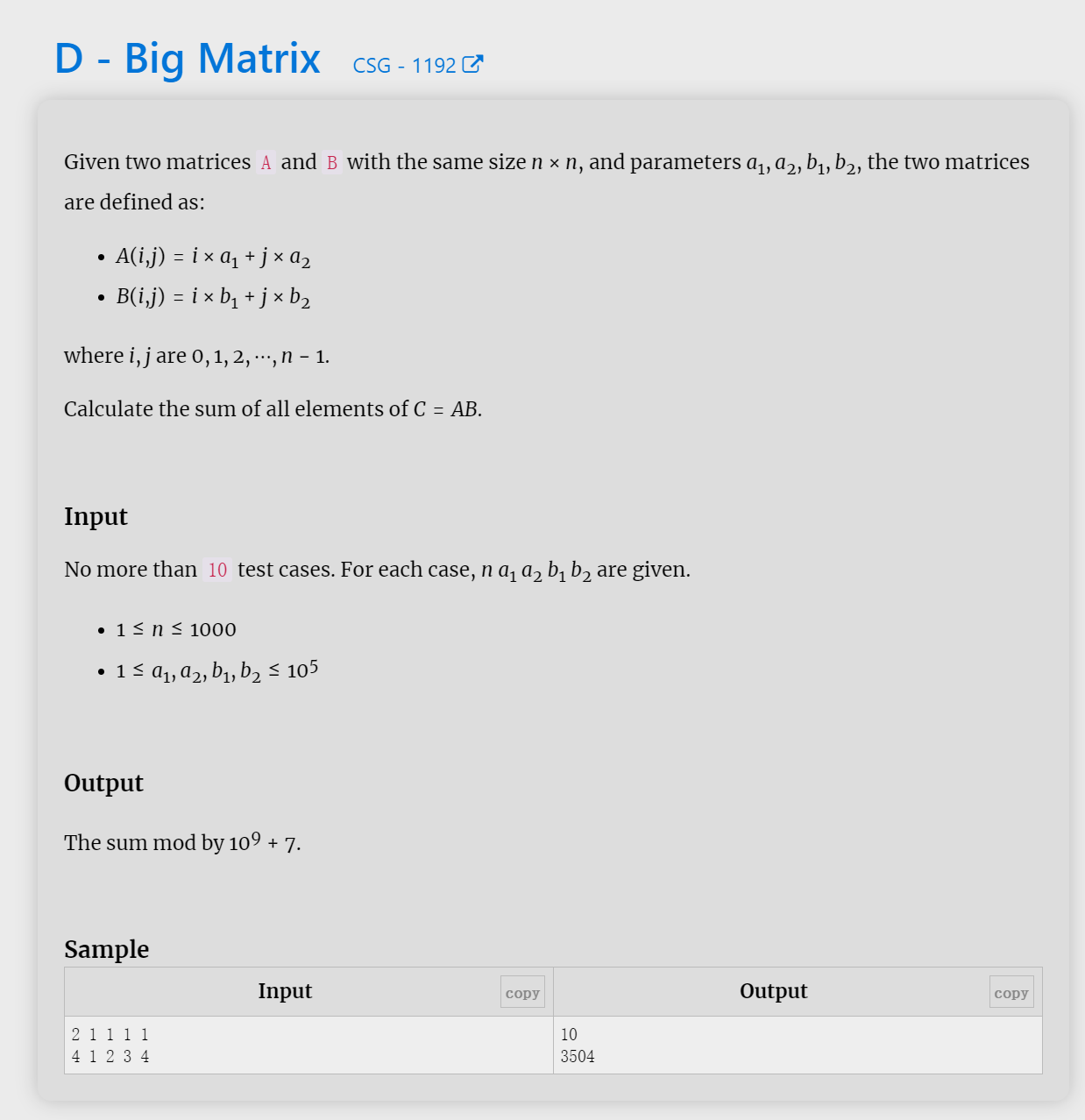这题的题目很简单，就是A和B俩个矩阵都是 n * n 的矩阵，矩阵中的所有值就是A的所有可能值和B的所有可能值，然后将A，B俩个矩阵相乘，得到一个新的矩阵C，然后将C中的所有元素加起来的结果输出即可

逻辑梳理

先看下图，我们就可以得到一个结论，就是A矩阵的第i列的和×B矩阵的第i行的和，ｉ从第一行到最后一行遍历完，每个结果都相加，就可以得到最终结果

那么，逻辑梳理完了，接下来我们来进入代码实现环节

代码实现

这里就直接放ＡＣ码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
const int mod = 1e9 + 7;
long long n, a1, a2, b1, b2;
long long a[1010][1010];
long long b[1010][1010];
long long c[1010], d[1010];
int main()
{
	while (cin >> n)
	{
		memset(c, 0, sizeof(c));
		memset(d, 0, sizeof(d));
		cin >> a1 >> a2 >> b1 >> b2;
		long long sum = 0, k = 0;
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				a[i][j] = i * a1 + j * a2;
				b[i][j] = i * b1 + j * b2;
			}
		}
		
		for (int j = 0; j < n; j++)
		{
			for (int i = 0; i < n; i++)
			{
				c[j] += a[i][j];
				c[j] %= mod;
			}
		}
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				d[i] += b[i][j];
				d[i] %= mod;
			}
		}
		for (int i = 0; i < n; i++)
		{
			sum += c[i] * d[i];
			sum %= mod;
		}
		cout << sum << endl;
	}
	return 0;
}