swift算法：最长回文子串

描述：给定一个字符串s，找到s中最长的回文子串，你可以假设s的最大长度是1000

例1：输入："babad"

          输出："bab"

          注意：“aba”也是一个有效答案

例2：输入："cbbd"

          输出："bb"

 

什么是回文字符串？

答：如果一个字符串正着读和反着读诗一样的，那么这个字符串就是回文字符串

 

1、中心扩展法

思路：找到字符串的中心，由于回文中心两侧互为镜像，然后向两边扩展，判断是否是同一个字符

时间复杂度：O(n^2)

具体实现：

class Solution {
    func longestPalindrome(_ s: String) -> String {
        
         if s.count == 0 {
            return ""
        }
        
        var start = 0, end = 0,i = 0
        
        while i<s.count {
            //回文中心为奇数的判断
            let len1 = find(s, i, i)
            //回文中心为偶数的判断
            let len2 = find(s, i, i+1)
            
            let len = max(len1, len2)
            if (len>end-start+1) {
                start = i-(len-1)/2
                end = i+len/2
                
            }
            i = i+1
        }
        let index1 = s.index(s.startIndex, offsetBy: start)
        let index2 = s.index(s.startIndex, offsetBy: end+1)
        return String(s[index1..<index2])
        
    }
    
//由回文中心向两边扩散
    func find(_ s : String, _ left : Int, _ right : Int)->Int{
        var left = left, right = right
       
        //循环判断是否为回文
        while ((left>=0) && (right<s.count) && (s[left]==s[right])) {
            //从中心向两边扩展
            left = left-1
            right = right+1
        }
        
        //返回最大长度
        
        return right-left-1
    }
    
    func max(_ a : Int, _ b : Int)->Int{
        return (a>b) ? a : b
    }

}

extension String{
    subscript(Index : Int)->String{
        let begin = self.startIndex
        let start = self.index(begin, offsetBy: Index)
        let end = self.index(begin, offsetBy: Index+1)
        let range : Range = start..<end
        return self.substring(with: range)
    }
}

缺点：在输入的字符串过长时，会导致运行时间变长，超出算法规定的时间限制，例如：输入"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaabcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"

2、马拉车(Manacher) 算法

什么是马拉车算法？

答：是中心扩展算法的升级算法，其精髓是将之前匹配过的字符串结果放到后面来使用

思路：

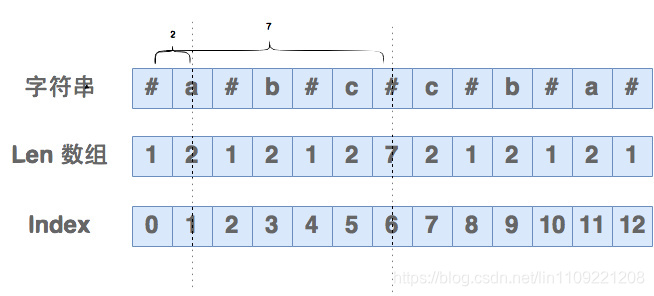
1）解决字符串长度的奇偶问题：需要对字符串做一个预处理，在所有的空隙位置（包括首尾）插入同样的字符，这样无论字符串是奇数还是偶数，都会使得处理过的字符串变成奇数长度

例如：123（长度为3，插入#）--> #1#2#3#（长度为7）

            abccba（长度为6，插入#）--> #a#b#c#c#b#a#（长度为13）

3）解决遍历过程中可能出现的越界：

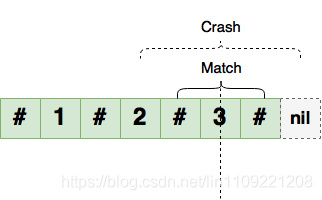
我们可以在首尾处各加入一个不同的字符，那么首尾就没有可能成为最长字符串的一部分，不会对我们的结果造成影响，所以用不匹配的结果来代替遍历造成的程序崩溃，是十分划算的

例如：123（长度为3，插入#）--> ~#1#2#3#+（长度为9）

            abccba（长度为6，插入#）--> ~#a#b#c#c#b#a#+（长度为15）

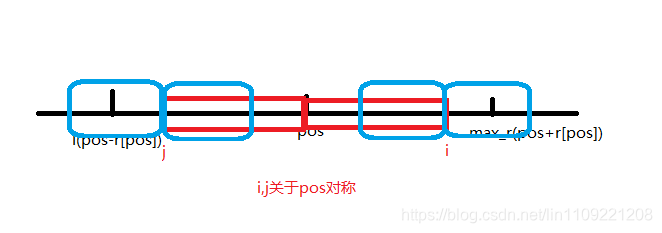
2）什么是回文半径？一个回文字符串中最左或最右位置的字符与其对称轴的距离 即为 回文半径，如下所示

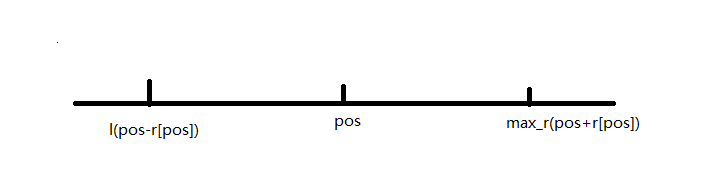
其中r[pos]表示以pos为中心点，向左右扩展回文串，所能达到的最大半径是多少

由于我们是从左往右扩展马拉车，所以从0～pos的所有数的最长半径已经做出来了，即 0～max_r 就是已知的最大范围

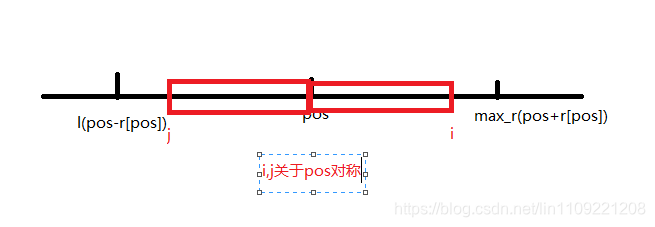
在这个基础上，我们在pos～max_r的范围内扩展i，并做j是关于pos的对称轴，r[j]是已知的

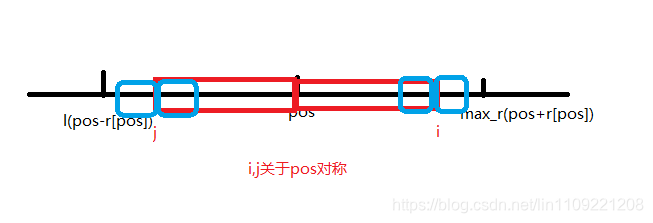
于是开始求r[i]，当 i+r[i]<max_r 时，用之前求过的r[j] 覆盖i这个位置，减少冗余计算，利用的是回文串的对称行

                            当 i+r[i]<max_r 时，已经不在可控范围内，则采用暴力扩展，再把pos转到i的位置继续执行上述操作

最后扫一遍r[i]求出max_r[i]，max_r[i]-1就是我们要的最长回文子串的长度

时间复杂度：O(n)

具体实现：

1）马拉车算法定义了一个回文半径数组 Len，用 Len[i] 表示以第 i 个字符为对称轴的回文串的回文半径。

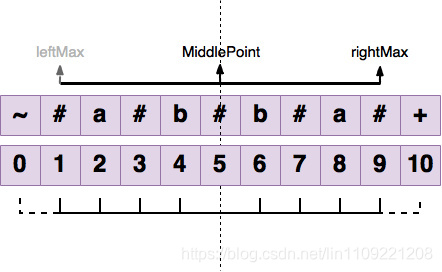
2）定义_rightMax_ 和 _middlePoint，_middlePoint 为有效的中心点，而 rightMax 为 middlePoint 对应的回文字符串的右边界，_middlePoint的位置不是固定的，会根据 i 与 rightMax和 Len[i]的关系变化

3）Len数组计算

第一种情况：i <= rightMax

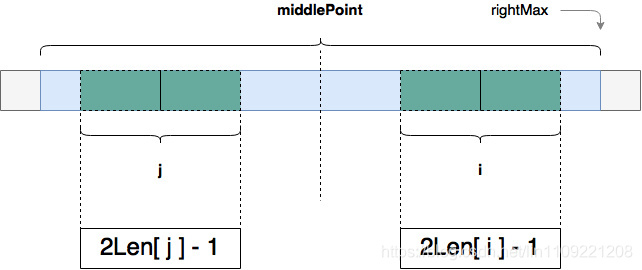
在上图中，i 和j对应的两个字回文串都被middle对应的回文串完全包括，暂且将middle当作已知最长回文串的中心点，j时之前已经求过的点，j的特点是与i关于middle对称，所以有关系式：2*middle-i，可以得到Len[i] == Len[j]

在遍历的过程中，j对应的字符串也有可能突破middle设立的leftMax~rightMax的围墙，

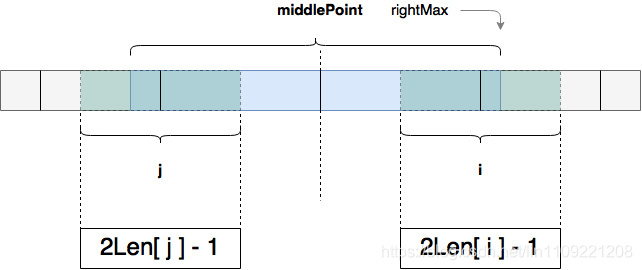
在这个的处理中，需要去掉围墙外的部分，重新匹配

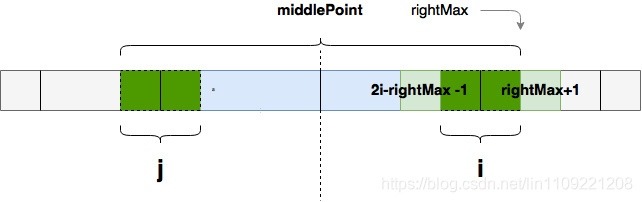
重新匹配完成后，无论i处的回文串长度有没有比middlePoint处的长度大，都需要更新middlePoint到i，更新rightMax为i处回文串的右边界

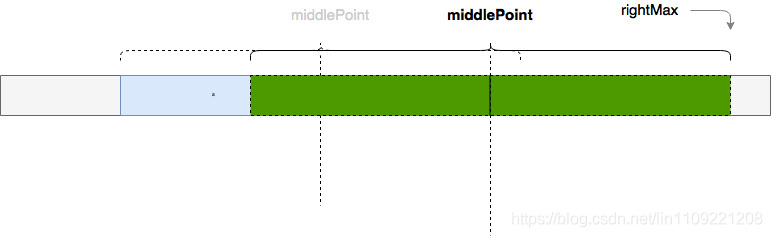
总结：

（1）Len[i]（有效）== min(rightMax - i, Len[2 * middlePoint - i])

（2）匹配前或者匹配后，出现 Len[i] > rightMax，需要更新 middlePoint 和 rightMax

第二种情况：i > rightMax

在这种情况下，i 并不在 middlePoint 的回文串范围内，也就无法省略部分的匹配步骤，只能重新匹配。匹配完后，同样需要更新 middlePoint 和 rightMax

class Solution {
    func longestPalindrome(_ s: String) -> String {
        
        //马拉车算法
        var charactersArr = Array<Character>()
        var resultString = String()
        var maxPoint = 0
        
        charactersArr.append("$")
        for character in s.characters {
            charactersArr.append("#")
            charactersArr.append(character)
        }
        charactersArr.append("#")
        charactersArr.append("%")
        
        //middlePoint 定义中心点，rightMax定义中心点的右边界
        var rightMax = 0, middlePoint = 0
        var lenArr = Array.init(repeating: 1, count: charactersArr.count)
        
        for i in 1 ..< 2 * s.characters.count + 2 {
            //当i在middlePoint的回文串范围内时，找到i的回文半径
            if rightMax > i {
                lenArr[i] = min(rightMax - i, lenArr[2 * middlePoint - i])
            }
            
            while charactersArr[i - lenArr[i]] == charactersArr[i + lenArr[i]] {
                lenArr[i] += 1
            }
            
            //当回文半径+i大于 middlePoint的右边界时，需要更新 中心点和右边界
            if lenArr[i] + i > rightMax {
                middlePoint = i
                
                rightMax = lenArr[i] + i
            }
            
            if lenArr[i] > lenArr[maxPoint] {
                maxPoint = i
            }
        }
        
        for i in stride(from: maxPoint - (lenArr[maxPoint] - 2), to: maxPoint + (lenArr[maxPoint] - 1), by: 2) {
            resultString.append(charactersArr[i])
        }
        
        return resultString
        
    }
    
    func max(_ a : Int, _ b : Int)->Int{
        return (a>b) ? a : b
    }
    func min(_ a : Int, _ b : Int)->Int{
        return (a<b) ? a : b
    }

}

extension String{
   func s_offset(_ offset : Int)->String.Index {
        return self.index(self.startIndex, offsetBy: offset)
    }
}

 

参考链接：Manacher's algorithm: 最长回文子串算法