1. 什么是频率编码?
频率编码是一种将时间、空间或特征域中的周期性模式转换为神经网络能够理解的数值表示的方法。它就像给神经网络配备了一副"频率眼镜",让网络能够看清数据中隐藏的节奏、周期和振动模式。
频率编码的核心思想对比:
|
编码类型 |
核心思想 |
好比人类理解 |
|
传统编码 |
直接使用原始数值 |
看钟表知道现在是3点 |
|
频率编码 |
揭示数值背后的周期规律 |
知道3点是下午茶时间,有周期性 |
2. 为什么需要频率编码?
2.1 现实世界中的频率现象
我们周围充满了各种频率模式:
-
时间频率:昼夜交替、季节变化、心跳节奏
-
空间频率:纹理图案、波浪形状、建筑韵律
-
信号频率:声音波形、电磁波、脑电波
2.2 传统神经网络的频率盲点
问题所在:
-
前馈神经网络难以捕捉长期周期性依赖
-
普通编码会丢失重要的相位信息
-
网络需要大量数据才能学习简单周期模式
解决方案:显式引入频率编码,让网络"先天"具备感知频率的能力
3. 正弦余弦频率编码
3.1 基本数学原理
想象一个旋转的轮子,轮子边缘某点的位置可以用正弦和余弦函数完美描述:
对于位置索引 pos 和维度 i,频率编码定义为:
其中:
-
pos:位置或时间索引
-
i:维度索引(从0开始)
-
:编码的总维度数
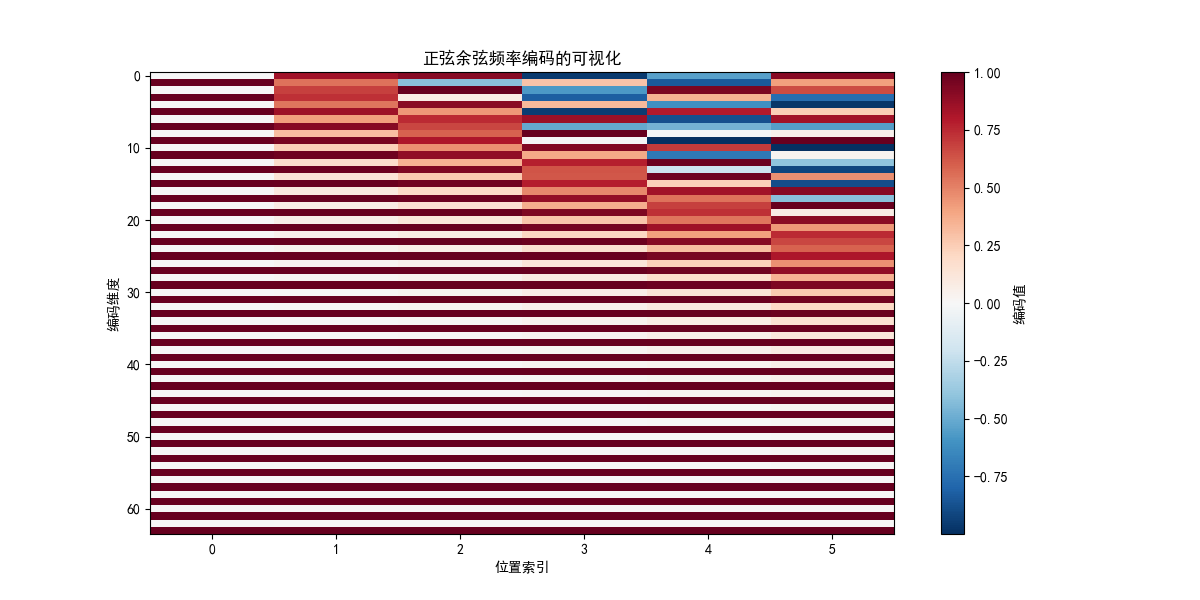
3.2 频率的几何解释
这个公式创造了一个美妙的几何结构:
-
不同频率:每个维度对应不同的频率
-
波长增长:随着 i 增大,波长呈几何级数增长
-
正交基:不同频率的编码近似正交
3.3 频率编码的数学性质
线性性质: 对于任意偏移量 k,位置 pos + k 的编码可以表示为位置 pos 编码的线性函数:
其中 M_k 是旋转矩阵,这个性质让神经网络能够轻松学习相对位置关系。
4. 傅里叶频率编码
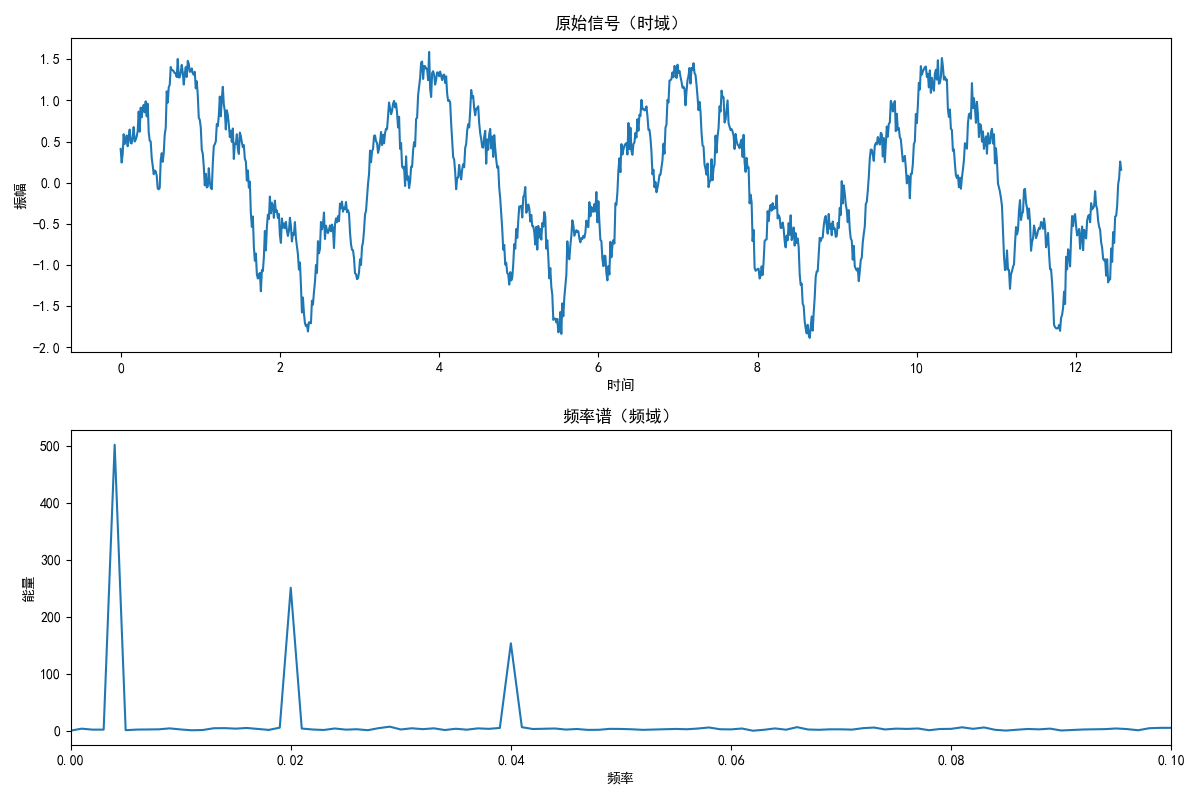
4.1 从时域到频域的转变
傅里叶变换的核心洞见:任何信号都可以分解为不同频率的正弦波组合。
连续傅里叶变换:
离散傅里叶变换:
4.2 傅里叶特征的优势
信息压缩:用少量频率成分近似复杂信号 噪声鲁棒性:高频噪声容易分离和过滤 物理意义明确:每个频率成分对应具体的物理过程
5. 频率编码在神经网络架构中的应用
5.1 Transformer中的位置编码
Transformer模型完全依赖频率编码来理解序列顺序:
编码特点:
-
每个位置有唯一的编码签名
-
相对位置关系通过线性变换保持
-
允许模型处理可变长度序列
5.2 图神经网络的频率编码
在图结构中,频率编码用于捕捉节点间的结构关系:
import networkx as nx
import torch
import torch.nn as nn
class GraphFrequencyEncoder:
"""图结构的频率编码"""
def laplacian_positional_encoding(self, graph, k):
"""基于拉普拉斯矩阵的特征向量进行编码"""
# 计算归一化拉普拉斯矩阵
laplacian = nx.normalized_laplacian_matrix(graph).astype(float)
# 特征分解
eigenvalues, eigenvectors = np.linalg.eigh(laplacian.toarray())
# 选择前k个最小非零特征值对应的特征向量
idx = eigenvalues.argsort()[:k]
positional_encoding = eigenvectors[:, idx]
return positional_encoding
5.3 卷积神经网络的频率视角
CNN天然具有频率处理能力:
-
浅层卷积核:捕捉高频边缘特征
-
深层卷积核:捕捉低频语义特征
-
池化操作:本质是低通滤波
6. 频率编码的数学深度
6.1 采样定理与混叠效应
奈奎斯特-香农采样定理:
生动比喻:如果电影帧率太低,我们会看到车轮似乎倒转 - 这就是频率混叠
在频率编码中,如果基础频率选择不当,也会出现类似的"认知混叠"。
6.2 频率域中的卷积定理
时域卷积 = 频域乘积:
重要意义:
-
复杂卷积运算简化为乘法
-
为频域神经网络提供理论基础
-
解释为什么CNN能有效处理图像
6.3 小波变换:多尺度频率分析
小波变换克服了傅里叶变换的固定窗口限制:
连续小波变换:
其中:
-
a:尺度参数(控制频率)
-
b:平移参数(控制位置)
-
:小波基函数
7. 高级频率编码技术
7.1 自适应频率学习
让网络自己学习最佳频率:
class AdaptiveFrequencyEncoding(nn.Module):
def __init__(self, max_seq_len, d_model):
super().__init__()
# 可学习的频率参数
self.frequencies = nn.Parameter(
torch.randn(d_model // 2) * 0.02
)
def forward(self, positions):
# positions: [seq_len]
angles = positions.unsqueeze(1) * self.frequencies.unsqueeze(0)
encoding = torch.zeros(positions.size(0), self.frequencies.size(0)*2)
encoding[:, 0::2] = torch.sin(angles)
encoding[:, 1::2] = torch.cos(angles)
return encoding
7.2 相对位置频率编码
考虑相对位置关系的改进编码:
这种编码直接编码位置对之间的关系,更适合注意力机制。
7.3 复数域频率编码
利用复数的天然频率特性:
复数编码可以同时表示振幅和相位信息。
8. 频率编码的实践指南
8.1 频率选择策略
|
数据类型 |
推荐频率范围 |
注意事项 |
|
自然语言 |
10-10000 |
考虑句子长度分布 |
|
时间序列 |
根据业务周期 |
避免混叠效应 |
|
图像数据 |
空间频率 |
考虑图像分辨率 |
|
图结构 |
谱域频率 |
基于图直径 |
8.2 频率编码的维度分配
合理的维度分配策略:
-
低频成分:分配更多维度,承载主要信息
-
高频成分:分配较少维度,捕捉细节特征
-
渐进式衰减:频率随维度增加而递减
8.3 常见陷阱与解决方案
频率混叠:
-
症状:模型对周期性模式学习困难
-
解决:确保采样频率足够高
频率过拟合:
-
症状:在训练集表现好,测试集差
-
解决:频率正则化,丢弃高频噪声
9. 频率编码的可视化理解
9.1 频率编码的拓扑结构
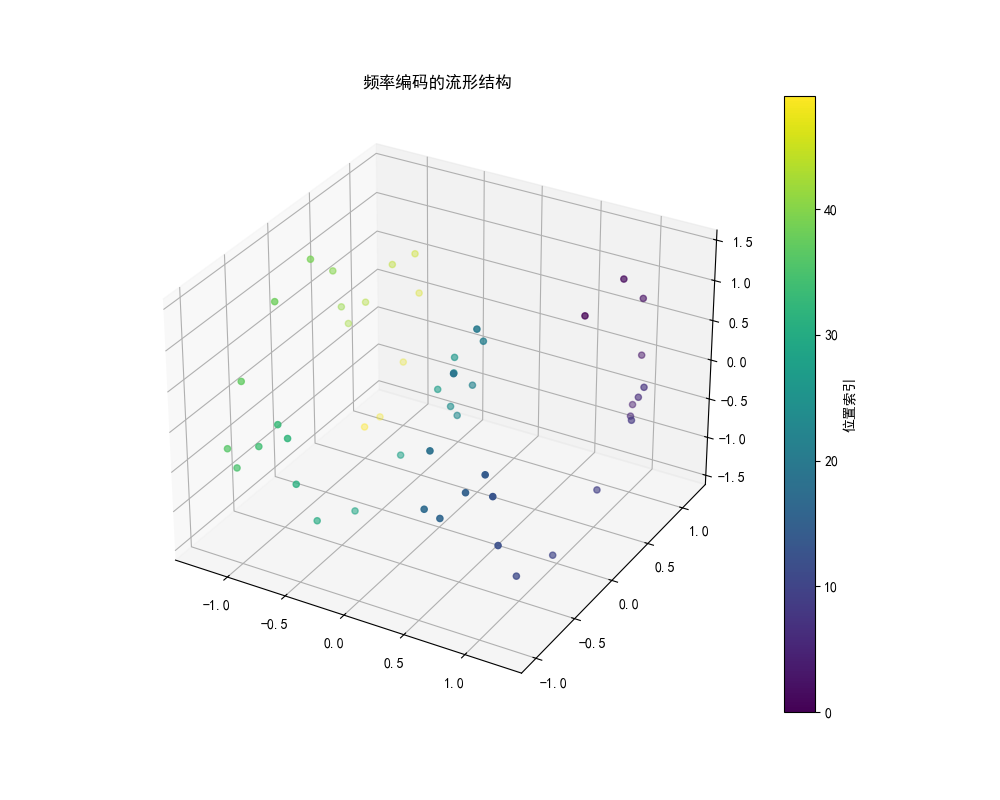
10. 未来发展方向
10.1 神经频率合成
让神经网络不仅理解频率,还能生成特定频率模式
10.2 量子频率编码
利用量子叠加原理实现超密集频率编码
10.3 生物启发频率编码
模仿大脑神经振荡的频率编码机制
总结
频率编码为神经网络打开了理解周期性世界的新窗口。通过将时间、空间和特征域中的周期性模式显式编码,我们赋予了神经网络感知节奏、预测周期和理解结构的能力。
关键收获:
-
频率编码让网络具备"先天"的频率感知能力
-
正弦余弦编码提供了优雅的数学框架
-
傅里叶视角揭示了信号的深层结构
-
正确的频率选择是成功应用的关键
频率编码不仅是技术工具,更是连接神经网络与物理世界周期性本质的桥梁。掌握频率编码,意味着让神经网络真正理解这个充满节奏和模式的世界。






















 3328
3328

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








