黑盒测试（一）

黑盒测试（一）

 

1.1 什么是黑盒测试

　　黑盒测试（Black Box Testing）又叫功能测试（Functional Testing），这是因为在黑盒测试中，主要关注于被测软件的功能实现，而不是内部逻辑。黑盒测试是与白盒测试截然不同的一个测试概念，也是在软件测试中使用得最早，也是最广泛的一类测试。在黑盒测试中，被测对象的内部结构，运作情况对测试人员是不可见的，测试人员对被测产品的验证主要是根据其规格，验证其与规格的一致性。就像对一台自动售货机，为了验证其能否自动售出货物，你可以指定需要购买的物品，塞入钱币，然后观测售货机能否输出正确的货物并找出正确的零钱。在这个过程中你不需要关注自动售货机是如何判定钱币数额，如何选择货物，如何找出零钱等内部操作。这是白盒测试关注的范围，黑盒测试关注的是结果。图1-1是黑盒测试的一个示意图。

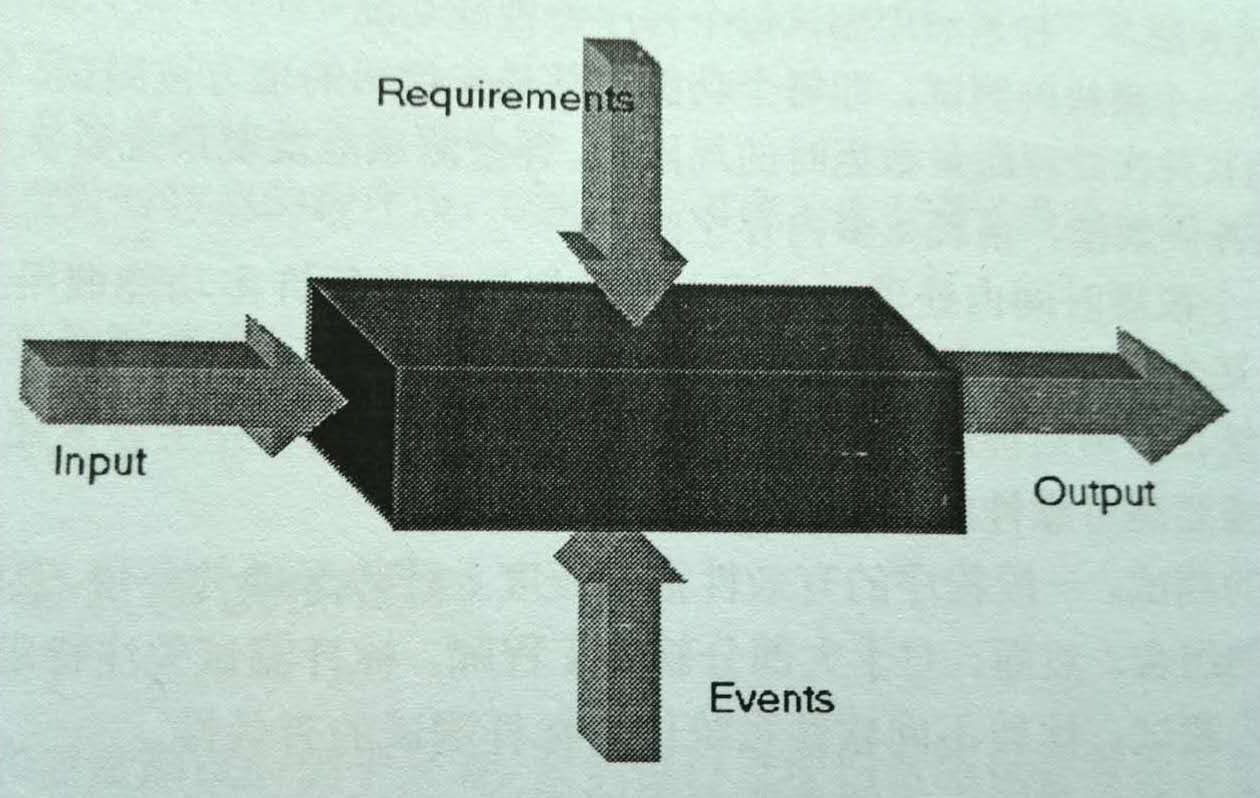
图1-1  黑盒测试示意图

　　黑盒测试试图发现以下类型的错误:

　　　　1）功能错误或遗漏；

　　　　2）界面错误；

　　　　3）数据结构或外部数据库访问错误；

　　　　4）性能错误；

　　　　5）初始化和终止错误。

 

1.2 为什么要进行黑盒测试

　　既然我们已经做了白盒测试，为什么还要进行黑盒测试？这不是浪费工作吗？

　　白盒测试在测试的早期采用，而黑盒测试主要用于测试的后期。黑盒测试故意不考虑控制结构，而是注意信息域。黑盒测试并不是白盒测试的替代品，而是用于辅助白盒测试发现其他类型的错误。黑盒测试用于回答以下问题：　

• • 如何测试功能的有效性？
  • 何种类型的输入会产生好的测试用例？
  • 系统是否对特定的输入值尤其敏感？
  • 如何分隔数据类的边界？
  • 系统能够承受何种数据率和数据量？
  • 特定类型的数据组合会对系统产生何种影响？

　　运用黑盒测试方法，可以导出满足以下标注的测试用例集：

　　　　1）所设计的测试用例能够减少达到合理测试所需的附加测试用例数；

　　　　2）所设计的测试用例能够告知某些类型错误的存在或不存在，而不是仅仅与特定测试相关的错误。