最近在刷算法题,发现之前写的斐波那契数列,用的是递归方式,感觉不是很好,尝试一下用别的方法。总共有4种,话不多说,贴代码。
法一:递归,时间复杂度是指数级。
public class Solution {
public int Fibonacci(int n) {
if(n==0)
return 0;
if(n==1)
return 1;
return Fibonacci(n-1)+Fibonacci(n-2);
}
}法二:动态规划,时间复杂度O(n)。
public class Solution { //这题尽量用循环,不要用递归
public int Fibonacci(int n) {
if(n==0)
return 0;
if(n==1)
return 1;
int one=0;
int two=1;
int N=0;
for(int i=2;i<=n;i++){
N=one+two;
one=two;
two=N;
}
return N;
}
}法三:斐波那契通项公式:,时间复杂度O(logn)。 //幂运算时间复杂度是logN
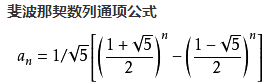





 本文探讨了斐波那契数列的四种不同实现方法,包括递归、动态规划、斐波那契通项公式以及矩阵乘法。递归方法虽然直观但效率低下,而动态规划和通项公式显著提高了时间效率,达到线性和对数级别。矩阵乘法提供了解决方案,进一步优化计算速度。
本文探讨了斐波那契数列的四种不同实现方法,包括递归、动态规划、斐波那契通项公式以及矩阵乘法。递归方法虽然直观但效率低下,而动态规划和通项公式显著提高了时间效率,达到线性和对数级别。矩阵乘法提供了解决方案,进一步优化计算速度。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1725
1725

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








