数据结构——树

 

1.AVL树（自平衡二叉查找树）

1）插入

avl树的插入操作每次可能会导致多个祖先失衡，但是它只要修改一次（最低的那个祖先节点），更高的祖先的高度也会复原。

解决办法：单旋，复杂度为O(1)；双旋（对应于”之“字形的情况）（实际并非简单地如此操作）（O(logn)）

具体实现：

 

2）删除

avl树的删除操作每次只可能导致一个祖先失衡（因为若删除一个节点导致失衡，则该节点一定在较矮的子树上，而计算树的高度时是由较高的子树决定的，故与它无关），但它改了这一个节点，可能又会引发其他节点的失衡，故相对于插入，删除操作更复杂。

解决办法：单旋（可能会达到O(logn)）、双旋（可能达到O(logn)）（实际并非如此简单地操作）

具体实现：

注意，起点为被删除节点的父亲。

 

3）3+4重构

把根节点及其以下两个节点重命名为a，b，c，把其下四棵子树重命名为t1，t2，t3，t4，按照中序遍历的方式，可得到t1->a->t2->b->t3->c->t4的结构。即BTS的单调性。无论如何调整，最终我们都要调整为如此结构。

 

具体实现：

 

关键——如何按照规则重命名：找出是左旋/右旋/左右旋/右左旋中的哪种情况，然后根据中序遍历的顺序确定重命名的节点位置。

 

4）总结

优点：查找、插入、删除等操作的最坏情况复杂度均为O(logn)。空间复杂度为O(n)。

缺点：借助高度或平衡因子，为此需改造元素结构，或额外封装；实测复杂度与理论值尚有差距；旋转花销大；单次动态调整后，全树的拓扑结构的变化量可能达到O(logn)（删除操作）。

 

2.伸展树

根据数据的局部性特点，通过伸展将节点v调整到树根的操作。

局部性：刚被访问过的数据，极有可能很快地再次访问

伸展：通过将节点v进行若干次旋转，最终移动到树根的过程。伸展采用的是Tajan的双层伸展方法，即先对v的祖父进行一次zig/zag操作，再对v的父亲节点进行zig/zag操作，从而使v到达祖父的位置。

好处：对于坏节点（e.g 只有左子树的二叉树的最后一个节点）的访问，每一次伸展都会将树高降低一半。分摊下去整个调整过程的每次调整时间复杂度为O(logn)。

 

1）具体实现

 

伸展树接口

与AVL的差别：AVL不用重写search()函数。

 

伸展功能

 

判断左/右孩子而进行相应操作的函数：它的具体变换过程与3+4重构很类似，不再赘述，这里采用拼接的函数形式略过。

           

 

 

搜索功能

伸展树区别于其他BST的本质特点：它的search()操作不是静态操作。其内部调用了splay()函数。

 

插入功能

过程：利用search（）函数搜索失败，会将最后一个节点t伸展到根节点的位置的特点，当t成为根节点时，把t和其左子树分为一部分，t的右子树分为一部分，此时引入要插入的节点v，让t和其左子树成为v的左子树，其右子树部分成为v的右子树，这样新节点v就被成功插入了。

 

 

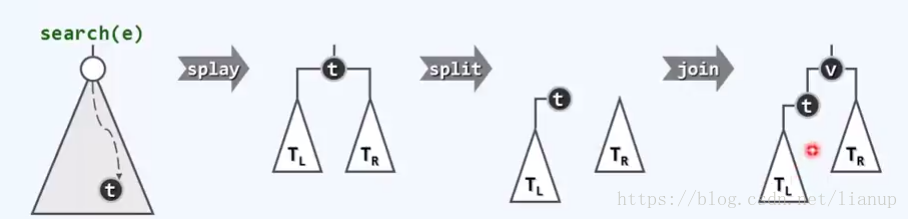
删除功能

过程：通过search()搜索到待删除的节点，并把该节点伸展到树根的位置。然后把该节点remove，再从右子树中找到最小的节点（此时该节点与被删除的节点非常接近，使得在后面局部性仍能得到应用），把它作为根的节点。

 

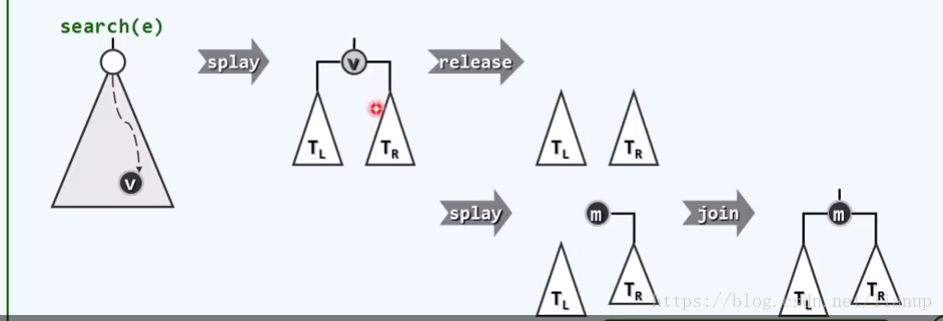
2）伸展树总结

 

优点：

1、与AVL树对比：无需记录节点高度或平衡因子，分摊复杂度为O(logn)。优于AVL树。

2、局部性强，缓存命中率极高（即k <<n << m）。在经过多次查找操作后，效率甚至可以达到自适应的O（logk）（经过多次查找，即经过多次伸展，热点数据几乎集中在树的顶部了。）任何连续的m次查找的复杂度为O（mlogk + nlogn）。

缺点：

1、仍不能保证单次最坏情况的出现，不适合于对单次查找效率敏感度高的场景。

 

3.B-树（平衡多路搜索树）

 

1）动机

弥合不同存储级别在访问速度上的差异，实现高效的I/O。它能做到对外存操作的代价与内存操作的代价大致相当。而BBST不能做到这一点。

 

2）结构

B树定义：m阶B-树，即m路平衡搜索树。（m>=2）

 

特点：所有叶节点的深度统一相等（外部节点的深度统一相等）；树高h=外部节点的深度；每个节点内有不超过m-1个关键码；

根节点：2<=分支数<=m；其余：m/2的向上取整<=分支数<=m；

外部节点：即叶节点中为空的，实际不存在的节点。

命名：又可称（m/2的向上取整，m）-树。（2，4）树在B-树中非常独特-->对应红黑树

 

BTNode结构：

 

B-树的结构：

 

3）具体实现

 

查找

关键：只载入必须的节点，尽可能减少I/O操作。

对于B-树的失败查找，必然失败于最底层叶节点某个下属的外部节点。

算法实现：

注意，这里的v = v->child[r+1]的选择原则，是返回不大于目标关键码的最大值，故为v->child[r+1]；

 

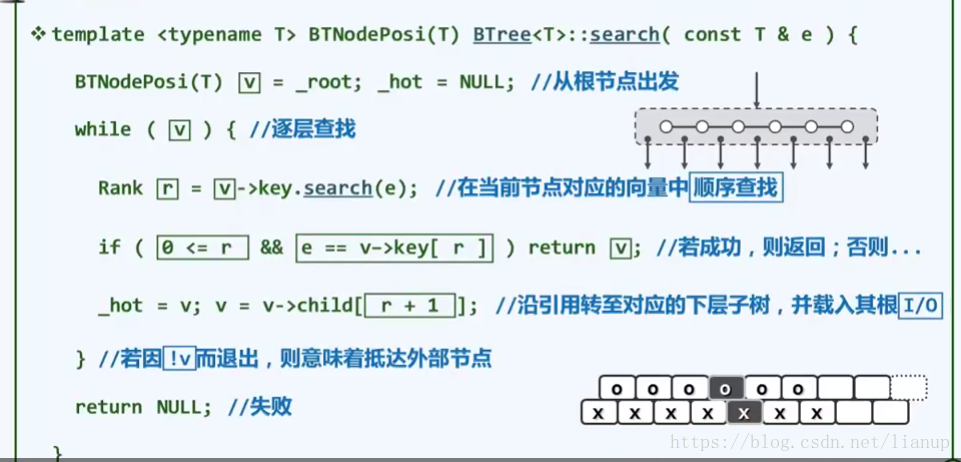
查找的复杂度：受树的高度所影响。

有N个内部节点，N+1个外部节点，就有N种成功的可能，N+1种失败的可能。

含N个关键码的m阶B-树的最大高度：内部节点包含的关键码尽可能少，h=O（logmN）。若取m=256，树高相对于BBST降低1/7。

含N个关键码的m阶B-树的最小高度：内部节点包含的关键码尽可能多。h>=logm（N+1）=Ω（logmN）。若取m=256，树高相对于BBST降低1/8.

 

插入

算法实现：根据分裂的次数，插入复杂度为O(h)。（h为B-树的高度）

 

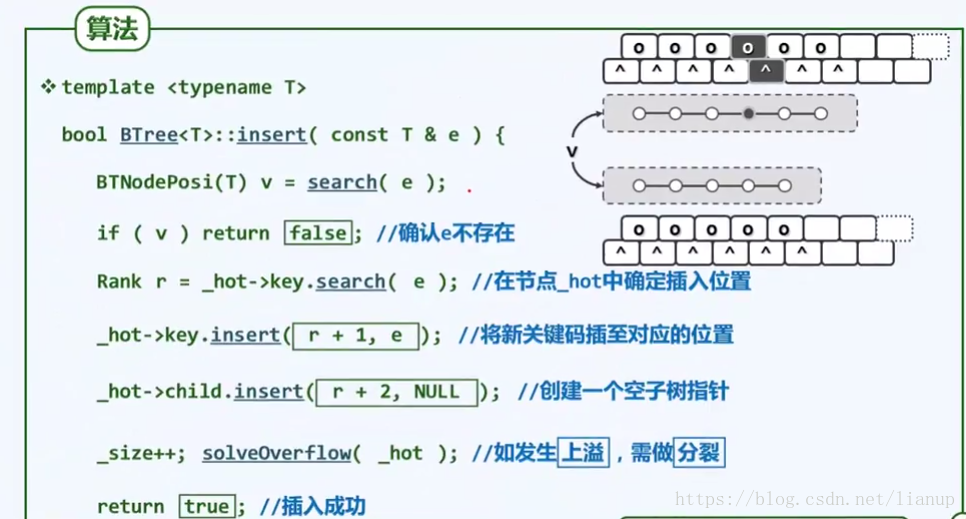
分裂操作实现：

中位数：在向量中，就是秩居中的元素，即A[0，n）中的A[n/2的上整]（e.g. A[0,5)中的A[2]，A[0，6)中的A[3]）

上溢可能会随着父节点传播，但只能逐层向上。父节点的上溢处理方法，也是继续分裂。最坏情况，是分类到根节点。

根节点的分裂操作：与其他节点不同的是，根节点上已经没有父节点，故中位数会独自上升成为一个新的根节点。这也是导致B-树高度上升的唯一情况。在新的根节点中，它只有两个分支。这也是为什么在B-树的规则中会有允许根节点有少于[m/2]条分支的存在。

 

删除

算法实现：

发生下溢时的处理操作有两种，分别是旋转和合并。优先级更高的是旋转。时间复杂度为O（h）（处理单次下溢时间复杂度为O(1)，下溢操作最多发生到根节点，次数为h）

 

旋转操作实现：

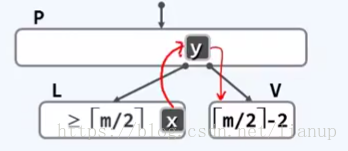
假设节点V在删除了一个元素后下溢，则它一定恰好包含[m/2]-2个关键码+[m/2]-1个分支。

此时可以从左边或右边的兄弟节点中，借一个元素。但直接借会破坏整个B-树的单调性。（左边节点元素<父节点元素<右边节点元素），故要进行以下操作：假设此时左边的兄弟节点有多余的元素可拿出，此时把父节点y放进V的最左边，把左边的兄弟节点的最大元素x放入y的位置，这样就不会破坏B-树的单调性。

用此种方案解决下溢，其他节点都不致再发生下溢，此种解决方案是彻底的。

 

合并操作实现：

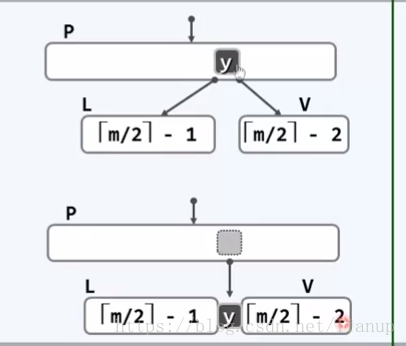
当V节点左右节点或者不存在，或左右节点的关键码均不足[m/2]个时，则可进行合并操作。

（注意，此时左右节点仍然存在其一，并且恰含[m/2]-1个关键码，以左兄弟节点为例子）

此时如果把V和左兄弟节点以及对应的父节点的关键码y合并，得到的关键码数也不会超过上限，因此，可以把它们三个合并。

此种解决方案可能会导致其父节点发生下溢。同时此种解决方案也是导致B-树高度下降的唯一可能。

 

4.红黑树

1）动机

图、向量、队列、链表等都是ephemeral data structure（短暂性数据结构），即它们不能保存以前的状态。而红黑树为persistent structure（一致性/持久性结构），它支持对历史版本的访问。

 

红黑树由来：

思考：若采用蛮力法成为一致性结构：每个版本独立保存，各版本入口自成一个搜索结构，设共有h个版本

得到的复杂度为：单次定位操作时间复杂度O(logh+logn)，生成所有版本累计O(h+n)时间/空间。

 

首次优化：若要降低生成所有版本累计时间空间复杂度到O（n+h*logn），则要利用各个版本之间的关联性。

实现方法：大量共享，少量更新。可使每个版本新增的复杂度就变为O（logn）。

 

再次优化：得到总体空间复杂度O(h+n)，单次操作时间复杂度为O（1）。

要求：就树形的拓扑结构，相邻版本之间的差异不能超过O(1)。即任何一次动态操作引发的结构变化量不致超过O(1)，但大多数的BBST如AVL树都不能做到，而红黑树能够做到。

 

2）结构

由红、黑两类节点组成的BST

特点：树根必为黑色；外部节点均为黑色；

其余节点：若为红，则只能有黑孩子（红之子、之父均为黑）；（控制红黑树的深度）

外部节点到根节点的途中黑节点数目相等。（控制红黑树的平衡性）

 

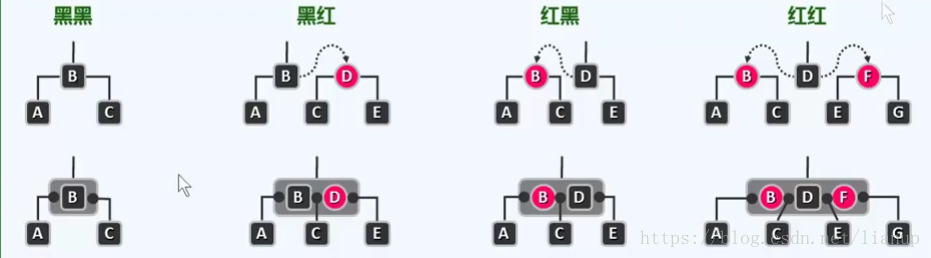
红黑树与B-树的关系：红黑树 = (2，4)树（4阶B树），故4阶B-树的特性均可以放到红黑树身上。

可把红黑树作一个提升变换来比较。把红孩子和黑父亲提升到同一个高度，并且将它们一起视作一个超级节点，会发现，红孩子和黑父亲的四种组合情况，分别对应4阶B-树超级节点的4种内部节点。

 

红黑树的接口定义：

注意，这里的节点x的高度是指黑高度

因此，高度更新的算法也要修改：

 

3）具体实现

为了便于观察规律，我们会把红黑树进行插入操作之前和之后对应为两棵B-树来理解。

插入

算法实现：

注意：按照BST常规算法插入x节点，x初始化为红色（这样红黑树的1、2、4准则都能满足，但3不一定能满足）插入后成为了一个末端节点。此时，可能会出现x与其父节点均为红色的情况，称为双红缺陷（double-red）。

 

 

双红缺陷改正

为了便于观察规律，分两种情况讨论，1种是x的叔父节点u为黑色，一种是x的叔父节点u为红色。

 

当x的叔父节点为黑色时：

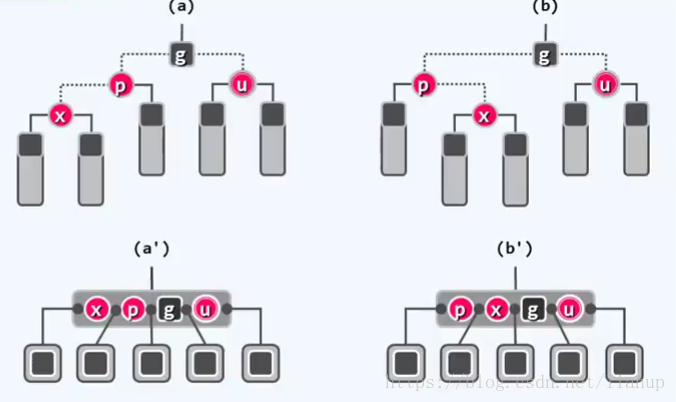
有四种情况，我们此时只列出两种，另外两种完全对称。此时在B-树中看到，x、p、g的四个孩子全为黑，且黑高度相同。

非法原因：从B-树的角度来理解，是因为在某个三叉节点中插入红关键码，使得原黑关键码不再居中。

 

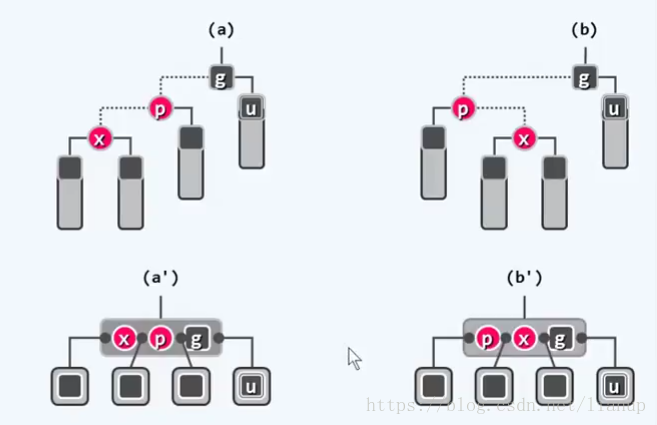
改正策略：1.参照AVL树算法，做局部3+4重构；2.重新染色，b转黑，a或c转红。

改正中的变化：从B-树的角度来看，B-树的拓扑结构并未发生改变，只不过是将节点颜色互换而已；从红黑树的角度看，红黑树的拓扑结构发生了变化，并且颜色也改变了。

改正步骤：将节点x、p、g及其四颗子树，按中序重新命名组合为：T0 < a < T1 < b < T2 < c < T3

并按照下图的模式重新进行拓扑链接

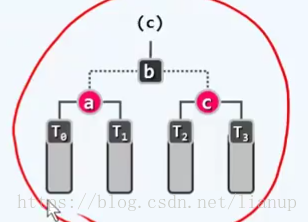
改正效果：只需一次调整；此种调整是红黑树的局部拓扑结构的改变，就全树的拓扑连接变化量而言，为O(1)。

 

当x的叔父节点u为黑色时：

同样地，有四种情况，这里只列出两种。

非法原因：从B-树的角度看，发生了上溢。

 

改正策略：p与u转黑，g转红。

改正中的变化：从B-树的角度看，B-树做了一次上溢处理，节点分裂，关键码g上升了一层，可能会引发父节点的双红缺陷，要一直修改到正确为止；从红黑树角度看，只不过是将节点颜色重新染色，拓扑结构并未发生改变。

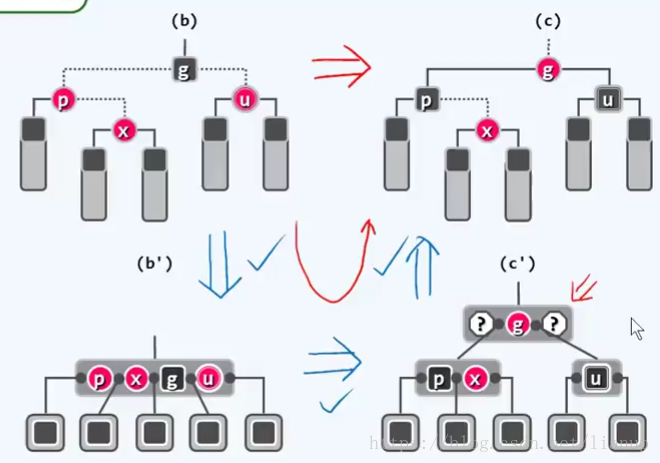
改正效果：尽管重染色造成的时间复杂度可能为O(logn)，但是拓扑连接变化量仍然为O(1)。

 

总结

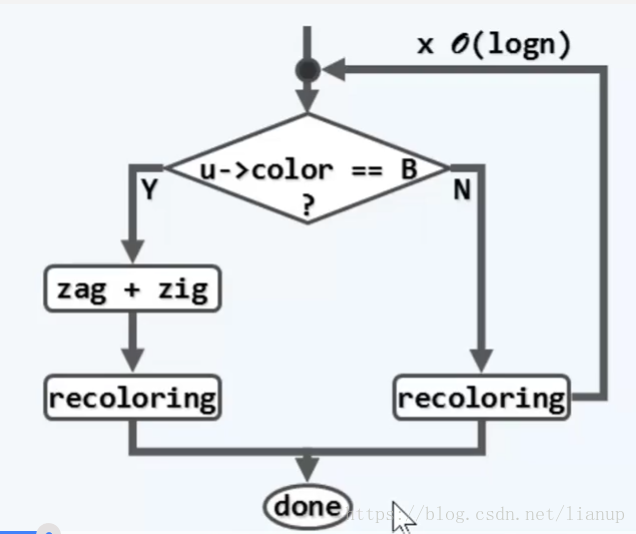
插入操作复杂度：插入操作的复杂度要看双红缺陷改正，而双红缺陷改正对应着下图两种情况。下图两种情况中，重染色和拓扑结构改变单次操作时间复杂度均为O(1)，故只要统计完成一个插入操作这两个操作的所有最大可能次数即可。

由图可知，在经过3+4重构后，插入操作一定会顺利完成，故3+4重构只做一次。而在双红缺陷中的第二种情况，重染色的时间复杂度可能高达O(logn)，故分析可知：

重染色次数：O(logn)；3+4重构次数：O(1)

时间复杂度为O(logn)

 

 

删除

算法实现：按照常规BST操作，将x节点删除后，将由其一个子节点r来替代。分两种情况讨论。若x与y之间有一个为红，则不会影响黑高度，只要进行简单的r节点染色操作即可；若x与r的颜色均为黑色，则会出现双黑缺陷。

 

双黑缺陷改正（double-black）

非法原因：从B-树角度分析，即原B-树中x所属节点下溢。故用B-树的下溢修复算法。

此时需要考察两个节点，x节点的父亲p（现r的父亲），以及r的兄弟s。情况有3种。

 

（BB-1）当s为黑，且至少有一个红孩子t时：

改正策略：3+4重构，t、s、p重命名为a、b、c；r保持黑，a，c染黑，b保持p的原色；

改正中的变化：从B-树的角度来看，是通过关键码的旋转来消除下溢。由于s至少有一个红孩子，所以s所在的超级节点的关键码个数充足，可以向x在的超级节点借出关键码，同时，s所在的超级节点中最右边的关键码保持p关键码的原色不变，所以不会再次造成双黑缺陷。

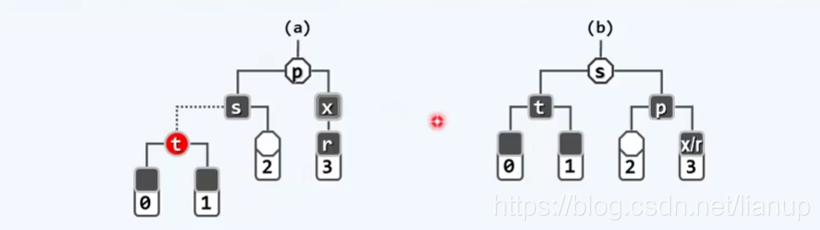
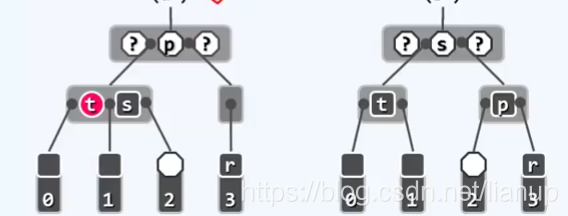
改正效果：红黑树的性质在全局中得以恢复，删除完成。

 

（BB-2A）当s及其两个孩子均为黑，p为红时：

改正策略：r保持黑；s转红；p转黑。

改正中的变化：从B-树的角度来看，等效于下溢节点与兄弟节点进行合并。

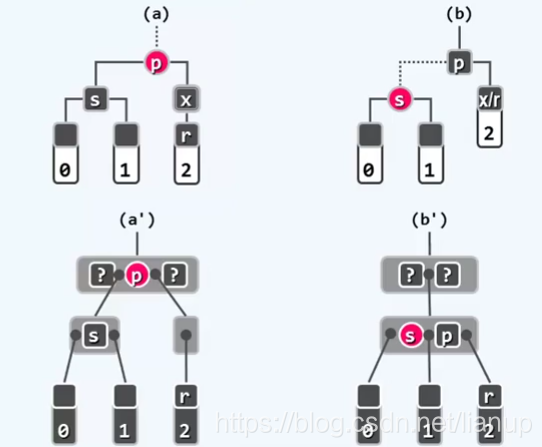
改正效果：红黑树的性质在全局中得以恢复，删除完成。此时p原来所在的超级节点不会下溢，因为p为红，意味着它至少有一个黑色的父节点和它组成超级节点，故原来的超级节点中至少还有一个黑节点，不会下溢。

 

（BB-2B）当s为黑，且两个孩子均为黑，p为黑：

改正策略：s变为红色，r和p保持黑色。

改正中的变化：从B-树的角度来看，是s和p用了合并操作。

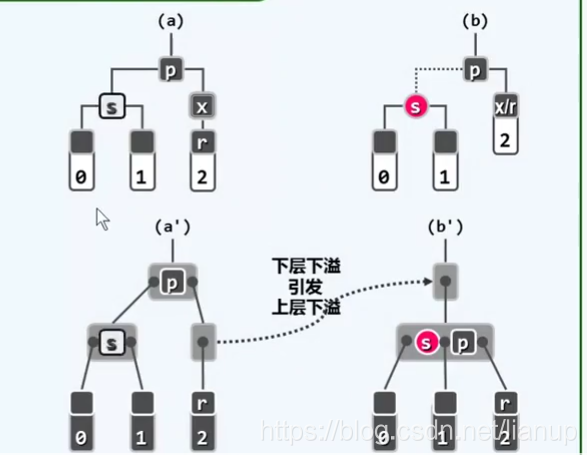
改正结果：由于此时p为黑色，从B-树角度看，b单独为一个超级节点，故会引发上一层的下溢，而这种下溢最多会有θ(logn)次。

 

（BB-3）S为红（其孩子均为黑）：

改正策略：红s转黑，黑p转红。（即做一次zig或zag操作）

改正中的变化：上述的改变并未消除黑高度的异常，但是可以使情况转化为BB-1或者BB-2A其中一种情况。

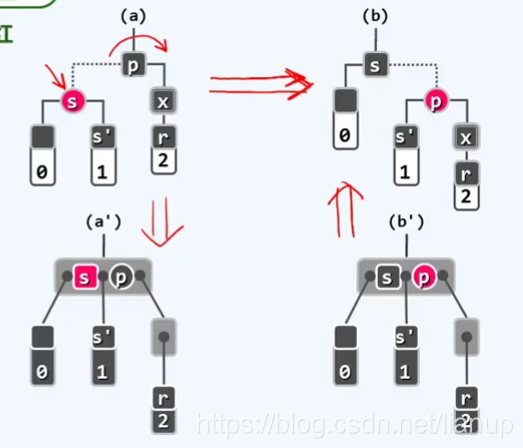
改正效果：经过改正后，且再经过一轮调整，就能够完成删除。

 

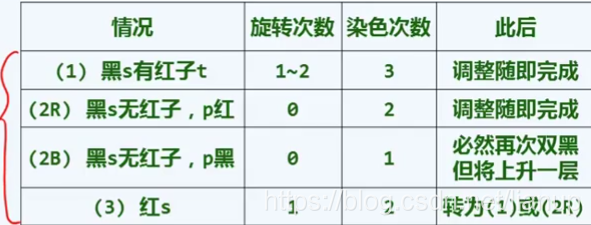
总结

时间复杂度：O(logn)

拓扑结构调整次数：O(1)