KMP算法

最新推荐文章于 2024-11-16 09:45:51 发布

不可不戒

最新推荐文章于 2024-11-16 09:45:51 发布

阅读量665

点赞数

分类专栏： KMP 算法

算法同时被 2 个专栏收录

26 篇文章

订阅专栏

KMP

14 篇文章

订阅专栏

KMP字符串模式匹配详解

来自优快云 A_B_C_ABC 网友

KMP字符串模式匹配通俗点说就是一种在一个字符串中定位另一个串的高效算法。简单匹配算法的时间复杂度为O(m*n);KMP匹配算法。可以证明它的时间复杂度为O(m+n).。

一．简单匹配算法

先来看一个简单匹配算法的函数：

int Index_BF ( char S [ ], char T [ ], int pos )

{

/* 若串 S 中从第pos(S 的下标0≤pos<StrLength(S))个字符

起存在和串 T 相同的子串，则称匹配成功，返回第一个

这样的子串在串 S 中的下标，否则返回 -1 */

int i = pos, j = 0;

while ( S[i+j] != '\0'&& T[j] != '\0')

if ( S[i+j] == T[j] )

j ++; // 继续比较后一字符

else

{

i ++; j = 0; // 重新开始新的一轮匹配

}

if ( T[j] == '\0')

return i; // 匹配成功返回下标

else

return -1; // 串S中(第pos个字符起)不存在和串T相同的子串

} // Index_BF

此算法的思想是直截了当的：将主串S中某个位置i起始的子串和模式串T相比较。即从 j=0 起比较 S[i+j] 与 T[j]，若相等，则在主串 S 中存在以 i 为起始位置匹配成功的可能性，继续往后比较( j逐步增1 )，直至与T串中最后一个字符相等为止，否则改从S串的下一个字符起重新开始进行下一轮的"匹配"，即将串T向后滑动一位，即 i 增1，而 j 退回至0，重新开始新一轮的匹配。

例如：在串S=”abcabcabdabba”中查找T=” abcabd”（我们可以假设从下标0开始）:先是比较S[0]和T[0]是否相等，然后比较S[1] 和T[1]是否相等…我们发现一直比较到S[5] 和T[5]才不等。如图：

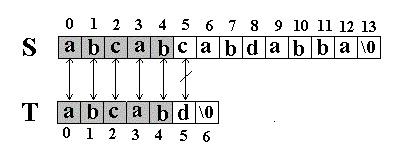
当这样一个失配发生时，T下标必须回溯到开始，S下标回溯的长度与T相同，然后S下标增1,然后再次比较。如图：

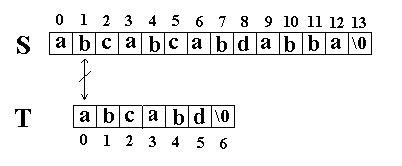
这次立刻发生了失配，T下标又回溯到开始，S下标增1,然后再次比较。如图：

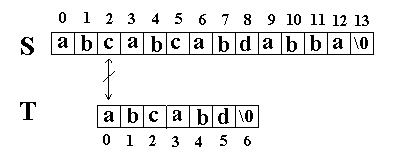
又一次发生了失配，所以T下标又回溯到开始，S下标增1,然后再次比较。这次T中的所有字符都和S中相应的字符匹配了。函数返回T在S中的起始下标3。如图：

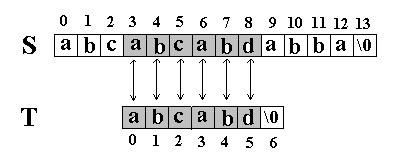
二. KMP匹配算法

还是相同的例子，在S=”abcabcabdabba”中查找T=”abcabd”，如果使用KMP匹配算法，当第一次搜索到S[5] 和T[5]不等后，S下标不是回溯到1，T下标也不是回溯到开始，而是根据T中T[5]==’d’的模式函数值（next[5]=2，为什么？后面讲），直接比较S[5] 和T[2]是否相等，因为相等，S和T的下标同时增加;因为又相等，S和T的下标又同时增加。。。最终在S中找到了T。如图：

KMP匹配算法和简单匹配算法效率比较，一个极端的例子是：

在S=“AAAAAA…AAB“(100个A)中查找T=”AAAAAAAAAB”, 简单匹配算法每次都是比较到T的结尾，发现字符不同，然后T的下标回溯到开始，S的下标也要回溯相同长度后增1，继续比较。如果使用KMP匹配算法，就不必回溯.

对于一般文稿中串的匹配，简单匹配算法的时间复杂度可降为O (m+n)，因此在多数的实际应用场合下被应用。

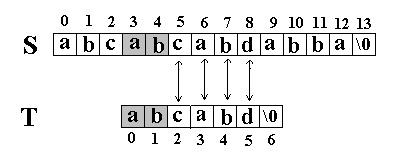
KMP算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。看前面的例子。为什么T[5]==’d’的模式函数值等于2（next[5]=2），其实这个2表示T[5]==’d’的前面有2个字符和开始的两个字符相同，且T[5]==’d’不等于开始的两个字符之后的第三个字符（T[2]=’c’）.如图：

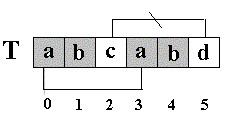
也就是说，如果开始的两个字符之后的第三个字符也为’d’,那么，尽管T[5]==’d’的前面有2个字符和开始的两个字符相同，T[5]==’d’的模式函数值也不为2，而是为0。

前面我说：在S=”abcabcabdabba”中查找T=”abcabd”，如果使用KMP匹配算法，当第一次搜索到S[5] 和T[5]不等后，S下标不是回溯到1，T下标也不是回溯到开始，而是根据T中T[5]==’d’的模式函数值，直接比较S[5] 和T[2]是否相等。。。为什么可以这样？

刚才我又说：“（next[5]=2），其实这个2表示T[5]==’d’的前面有2个字符和开始的两个字符相同”。请看图：因为，S[4] ==T[4]，S[3] ==T[3]，根据next[5]=2，有T[3]==T[0]，T[4] ==T[1]，所以S[3]==T[0]，S[4] ==T[1]（两对相当于间接比较过了），因此，接下来比较S[5] 和T[2]是否相等。。。

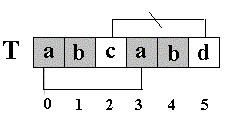
有人可能会问：S[3]和T[0]，S[4] 和T[1]是根据next[5]=2间接比较相等，那S[1]和T[0]，S[2] 和T[0]之间又是怎么跳过，可以不比较呢？因为S[0]=T[0]，S[1]=T[1]，S[2]=T[2]，而T[0] != T[1], T[1] != T[2],==> S[0] != S[1],S[1] != S[2],所以S[1] != T[0],S[2] != T[0]. 还是从理论上间接比较了。

有人疑问又来了，你分析的是不是特殊轻况啊。

假设S不变，在S中搜索T=“abaabd”呢？答：这种情况，当比较到S[2]和T[2]时，发现不等，就去看next[2]的值，next[2]=-1，意思是S[2]已经和T[0] 间接比较过了，不相等，接下来去比较S[3]和T[0]吧。

假设S不变，在S中搜索T=“abbabd”呢？答：这种情况当比较到S[2]和T[2]时，发现不等，就去看next[2]的值，next[2]=0，意思是S[2]已经和T[2]比较过了，不相等，接下来去比较S[2]和T[0]吧。

假设S=”abaabcabdabba”在S中搜索T=“abaabd”呢？答：这种情况当比较到S[5]和T[5]时，发现不等，就去看next[5]的值，next[5]=2，意思是前面的比较过了，其中，S[5]的前面有两个字符和T的开始两个相等，接下来去比较S[5]和T[2]吧。

总之，有了串的next值，一切搞定。那么，怎么求串的模式函数值next[n]呢？（本文中next值、模式函数值、模式值是一个意思。）

三. 怎么求串的模式值next[n]

定义：

（1）next[0]= -1 意义：任何串的第一个字符的模式值规定为-1。

（2）next[j]= -1 意义：模式串T中下标为j的字符，如果与首字符

相同，且j的前面的1—k个字符与开头的1—k

个字符不等（或者相等但T[k]==T[j]）（1≤k<j）。

如：T=”abCabCad” 则 next[6]=-1，因T[3]=T[6]

（3）next[j]=k 意义：模式串T中下标为j的字符，如果j的前面k个

字符与开头的k个字符相等，且T[j] != T[k] （1≤k<j）。

即T[0]T[1]T[2]。。。T[k-1]==

T[j-k]T[j-k+1]T[j-k+2]…T[j-1]

且T[j] != T[k].（1≤k<j）;

(4) next[j]=0 意义：除（1）（2）（3）的其他情况。

举例：

01）求T=“abcac”的模式函数的值。

next[0]= -1 根据（1）

next[1]=0 根据 (4) 因（3）有1<=k<j;不能说，j=1,T[j-1]==T[0]

next[2]=0 根据 (4) 因（3）有1<=k<j;（T[0]=a）!=（T[1]=b）

next[3]= -1 根据 (2)

next[4]=1 根据 (3) T[0]=T[3] 且 T[1]=T[4]

即

下标	0	1	2	3	4
T	a	b	c	a	c
next	-1	0	0	-1	1

若T=“abcab”将是这样：

下标	0	1	2	3	4
T	a	b	c	a	b
next	-1	0	0	-1	0

为什么T[0]==T[3],还会有next[4]=0呢, 因为T[1]==T[4], 根据 (3)” 且T[j] != T[k]”被划入（4）。

02）来个复杂点的，求T=”ababcaabc” 的模式函数的值。

next[0]= -1 根据（1）

next[1]=0 根据(4)

next[2]=-1 根据 (2)

next[3]=0 根据 (3) 虽T[0]=T[2] 但T[1]=T[3] 被划入（4）

next[4]=2 根据 (3) T[0]T[1]=T[2]T[3] 且T[2] !=T[4]

next[5]=-1 根据 (2)

next[6]=1 根据 (3) T[0]=T[5] 且T[1]!=T[6]

next[7]=0 根据 (3) 虽T[0]=T[6] 但T[1]=T[7] 被划入（4）

next[8]=2 根据 (3) T[0]T[1]=T[6]T[7] 且T[2] !=T[8]

即

下标	0	1	2	3	4	5	6	7	8
T	a	b	a	b	c	a	a	b	c
next	-1	0	-1	0	2	-1	1	0	2

只要理解了next[3]=0，而不是=1，next[6]=1，而不是= -1，next[8]=2，而不是= 0，其他的好象都容易理解。

03) 来个特殊的，求 T=”abCabCad” 的模式函数的值。

下标	0	1	2	3	4	5	6	7
T	a	b	C	a	b	C	a	d
next	-1	0	0	-1	0	0	-1	4

next[5]= 0 根据 (3) 虽T[0]T[1]=T[3]T[4],但T[2]==T[5]

next[6]= -1 根据 (2) 虽前面有abC=abC,但T[3]==T[6]

next[7]=4 根据 (3) 前面有abCa=abCa,且 T[4]!=T[7]

若T[4]==T[7]，即T=” adCadCad”,那么将是这样：next[7]=0, 而不是= 4,因为T[4]==T[7].

下标	0	1	2	3	4	5	6	7
T	a	d	C	a	d	C	a	d
next	-1	0	0	-1	0	0	-1	0

如果你觉得有点懂了，那么

练习：求T=”AAAAAAAAAAB” 的模式函数值，并用后面的求模式函数值函数验证。

意义：

next 函数值究竟是什么含义，前面说过一些，这里总结。

设在字符串S中查找模式串T，若S[m]!=T[n],那么，取T[n]的模式函数值next[n],

1. next[n]= -1 表示S[m]和T[0]间接比较过了，不相等，下一次比较 S[m+1] 和T[0]

2. next[n]=0 表示比较过程中产生了不相等，下一次比较 S[m] 和T[0]。

3. next[n]= k >0 但k<n, 表示,S[m]的前k个字符与T中的开始k个字符已经间接比较相等了，下一次比较S[m]和T[k]相等吗？

4. 其他值，不可能。

四. 求串T的模式值next[n]的函数

说了这么多，是不是觉得求串T的模式值next[n]很复杂呢？要叫我写个函数出来，目前来说，我宁愿去登天。好在有现成的函数，当初发明KMP算法，写出这个函数的先辈，令我佩服得六体投地。我等后生小子，理解起来，都要反复琢磨。下面是这个函数:

void get_nextval(const char *T, int next[])

{

// 求模式串T的next函数值并存入数组 next。

int j = 0, k = -1;

next[0] = -1;

while ( T[j/*+1*/] != '\0' )

{

if (k == -1 || T[j] == T[k])

{

++j; ++k;

if (T[j]!=T[k])

next[j] = k;

else

next[j] = next[k];

}// if

else

k = next[k];

}// while

这里是我加的显示部分

// for(int i=0;i<j;i++)

//{

// cout<<next[i];

//}

//cout<<endl;

}// get_nextval　

另一种写法，也差不多。

void getNext(const char* pattern,int next[])

{

next[0]= -1;

int k=-1,j=0;

while(pattern[j] != '\0')

{

if(k!= -1 && pattern[k]!= pattern[j] )

k=next[k];

++j;++k;

if(pattern[k]== pattern[j])

next[j]=next[k];

else

next[j]=k;

}

这里是我加的显示部分

// for(int i=0;i<j;i++)

//{

// cout<<next[i];

//}

//cout<<endl;

}

循环节问题

它还能用来求周期字符串的循环节HDU1358:

性质:

当且仅当len%(len-next[len])==0时,str[next[len]~len-1]为最小循环节

要证明它需要说明3点:

1.一个字符串str是周期串,假设s1为它的循环节,则str=s1 s1...s1(n个)

推导出=>len%(len-next[len])==0成立.

2.next[len]~len-1为s1 ,len%(len-next[len])==0时

推导出=>str为周期串,s1为最小循环节

3.如何保证是最小的.

证明:

1.由next的性质知道,s[1~next[len]-1]与s[1~len-1]有最长的相等的前缀和后缀s,很显然s就是n-1个s1了.

2.设s1的长度为L,由于len%L==0 , str可以分解成若干个长度为L的小串,设它们从左到右依次为

a₁, a₂... a_n

根据匹配关系得

a₁=a₂;

a₂=a₃;

a_n-1=a_n;

因此a₁=a₂=a₃...=a_n;

3.next[len]保证了前缀与后缀最大化,如果循环节s1存在而s1内还有循环节s1',则next[len]可以向后移动,与定义矛盾.

-----------------------

k m x j i

由上，next【i】=j，两段红色的字符串相等（两个字符串完全相等），s[k....j]==s[m....i]

设s[x...j]=s[j....i](xj=ji)

则可得，以下简写字符串表达方式

kj=kx+xj;

mi=mj+ji;

因为xj=ji，所以kx=mj，如下图所示

-------------

k m x j

看到了没，此时又重复上面的模型了，kx=mj，所以可以一直这样递推下去

所以可以推出一个重要的性质len-next[i]为此字符串的最小循环节(i为字符串的结尾)，另外如果len%(len-next[i])==0,此字符串的最小周期就为len/(len-next[i]);

大概的解法就是使用kmp来做，利用next数组来处理。这里先简单滴介绍下怎样根据next数组计算最大的循环节。

当所给字符串中无循环节时，如abcdeab ，我们求出其next数组的对应值（注意按照标准的next数组要多求一位，计算时向后推一位计算，因为标准的next数组第n个数表示的是第n-1个字符的匹配情况），然后用字符串长度L-next[L]即可，此时上例中显然 next[L]为2，即为多出的ab，所以循环节就是7-2=5；

当所给字符串中有多个字符串时，如abxabxabxab,此时 next[L]为8,11-8=3，亦是循环节，我们可以看出 L-next[L]就是循环节，其实在一个多个循环节的字符串中，除了第一个循环节中字符外，其他每个位置的下标n-next[n]都是循环节（第一个循环节中的最后一个位置也可）。

于是乎，我们就可以得到循环节为 L-next[L]，然后计算出按题意补全后的字符串长度应为 L-next[L]的整数倍，若 L%（ L-next[L]）==0 自然不用补字符了，否则补全后的字符串长度应为( L/（ L-next[L]） +1)* L-next[L]，然后用之减去L得解。

相等的循环同构问题

hdu3374 string problem

分析:

　　最大和最小的循环同构字符串可以分开处理,求位置可以利用最小最大表示法(03wc论文周源)

　　求出现的次数可以用kmp扫一遍,但利用循环节可以更快地得到答案.

性质:

　　字符串str由k个最小循环节s1组成,则它的相等循环同构数为k.

证明:

　　设相等循环同构数为p,我们可以利用循环节s1构造出k个相等的循环同构,于是p>=k;

　　下面证明p<=k:

　　　　如果p>k

　　　　假设在移动完s1到尾部前,出现了相同的循环同构串,不妨设此时移动的串为s2,

　　　　则利用循环节性质2第1种情况的推理方法可以知道s2为字符串的一个循环节

　　　　且s2的长度<s1,与s1为最小循环节的条件矛盾,因此p<=k.

　　于是p只能等于k.

拓展KMP

　　有很长一段时间单纯地以为拓展kmp只是kmp倒过来跑,后来发现很多问题其实无法转换成kmp解决,于是怒学了一下拓展kmp.

　　首先比较一下kmp和拓展kmp解决的问题:

　　kmp解决了求所有主串的前缀pre[i] (0<=i<n)的后缀与模式串前缀的最大匹配长度问题;

　　拓展kmp解决了所有主串的后缀suf[i]的前缀,与模式串前缀的最大匹配长度问题.

 1 void getNext() {
 2     int l = 1, r = -1, i, j;
 3 
 4     for (next[0] = 0, i = 1; p[i]; ++i) {
 5         if (i + next[i - l] - 1 < r) next[i] = next[i - l];
 6         else {
 7             for (j = max(r - i + 1, 0); p[i + j] && p[i + j] == p[j]; ++j);
 8             next[i] = j; l = i; r = i + j - 1;
 9         }
10     }
11     next[0] = i;
12 }

　　设模式串为str;

　　定义next[i]为 str 与它的后缀suf[i]的最大公共前缀长度.

　　r是当前已经确定匹配区间的最右端点,l是对应的左端点,即 r=l+next[l]-1;

　　当要求next[i]时

　　根据 next定义 str[ l , l+next[l]-1 ] == str[ 0 , next[l]-1 ];

　　得到 str[ i , l+next[l]-1 ] == str[ i-l , next[l]-1 ];

　　设s1=str[ i , l+next[l]-1 ];

　　讨论以下情况：

　　1. 若 i在 [l,r] 区间内

　　　next[i-l]的值我们已经知道,这时候需要讨论:

　　　　如果 next[i-l] 小于 s1 的长度,那么可以知道在下标为 next[i-l] 的位置必定会失配,于是next[i]=next[i-l];

　　　　如果 next[i-l] 大于或等于 s1 的长度,那么直到r位置,我们都可以确定已经匹配上了,接下来需要确定r后面

　　　　位置的匹配情况,而此时i已经匹配了r-i+1的长度,next[i]从这个值开始计数就可以了,计数完成后i+next[i]-1

　　　　已经大于r,因此要更新 r=i+next[i]-1 , l=i ;

　　2.若 i不在[l,r]的区间内,即 i > r, 前面得到的信息无法用到,于是我们需要从头将str[i]与str[0]进行匹配,当然也要记得更新l,r.

　复杂度：

　　　　2个循环变量i,j都是单调增的,而他们最多增加n次,因此复杂度是线性的.

　　拓展kmp求循环节的方法参考kmp求循环节部分.

　　知道这些后可以来解决这个问题.

next[]数组的运用。

这里需要深刻理解next数组的含义，所以需要花费一定的功夫去弄懂这些。。

对于next数组，经过3天的学习，有了一定的认识。自己总结一下吧。

首先，求next数组有两种方法。第一种是严蔚敏教授那本数据结构上的求法。代码如下：

[cpp]view plaincopy 
   
 void getnext(const char *s)  
 {  
     int i = 0, j = -1;  
     nextval[0] = -1;  
     while(i != len)  
     {  
         if(j == -1 || s[i] == s[j])  
             nextval[++i] = ++j;  
         else  
             j = nextval[j];  
     }  
 }  

这种求法的含义是：

next[i]代表了前缀和后缀的最大匹配的值（需要彻底明白这点，相当重要）

另外一种是对这种算法的改进版本，代码如下：

[cpp]view plaincopy 
   
 void getnext(const char *p) //前缀函数(滑步函数)  
 {  
     int i = 0, j = -1;  
     nextval[0] = -1;  
     while(i != len)  
     {  
         if(j == -1 || p[i] == p[j]) //(全部不相等从新匹配 || 相等继续下次匹配)  
         {  
             ++i, ++j;  
             if(p[i] != p[j]) //abcdabce  
                 nextval[i] = j;  
             else //abcabca  
                 nextval[i] = nextval[j];  
         }  
         else  
             j = nextval[j]; //子串移动到第nextval[j]个字符和主串相应字符比较  
     }  
 }  