tensorflow中常用学习率更新策略
微信公众号:幼儿园的学霸
个人的学习笔记,关于OpenCV,关于机器学习, …。问题或建议,请公众号留言;
神经网络训练过程中,根据每batch训练数据前向传播的结果,计算损失函数,再由损失函数根据梯度下降法更新每一个网络参数,在参数更新过程中使用到一个学习率(learning rate),用来定义每次参数更新的幅度。
过小的学习率会降低网络优化的速度,增加训练时间,过大的学习率可能导致网络参数在最终的极优值两侧来回摆动,导致网络不能收敛。实践中证明有效的方法是设置一个根据迭代次数衰减的学习率,可以兼顾训练效率和后期的稳定性。
目录
学习率
使用TensorFlow训练一个模型时,我们需要通过优化函数来使得我们训练的模型损失值达到最小,常用的优化算法有随机梯度下降、批量梯度下降,而在使用优化算法的时候,我们都需要设置一个学习率(learning rate),而学习率的设置在训练模型的时候也是非常重要的,因为学习率控制了每次更新参数的幅度。如果学习率太大就会导致更新的幅度太大,就有可能会跨过损失值的极小值(不说最小值的原因,是因为有可能是局部的最小值),最后可能参数的极优值会在参数的极优值之间徘徊,而取不到参数的极优值。如果学习率设置的太小,就会导致的更新速度太慢,从而需要消耗更多的资源来保证获取到参数的极优值。
学习率设置大了震荡不收敛,设置小了,收敛速度太慢,时间成本高.
下面我们使用tensorflow设置损失函数为y=(w+1)^2, 初始w=5, 显然,我们知道最优的值w=-1,此时loss=0,但是代码能否通过训练找出这个最优的值呢?我们尝试不同的学习率来观察loss值、w值输出的变化情况,以此解析学习率究竟是如何影响参数的更新。
#!/usr/bin/env python3
#coding=utf-8
#============================#
#Program:different_learnrate.py
#
#Date:19-12-20
#Author:liheng
#Version:V1.0
#============================#
#coding:utf-8
"""
设置损失函数为 loss = (w+1)^2
令w的初值为常数5,反向传播就是求最优的w,即求最小的loss对应的w值
"""
import tensorflow as tf
# 定义待优化变了w,赋初值5
w = tf.Variable(tf.constant(5,dtype=tf.float32))
#定义损失函数loss
loss = tf.square(w+1) # 则梯度=2*(w+1)=2w+2
#定义反向传播算法
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(loss)
print('step\tw\tloss')
with tf.Session() as sess:
# 初始化所有变量
init_op = tf.group(tf.global_variables_initializer(), tf.local_variables_initializer())
sess.run(init_op)
# 设置训练轮数为5
for i in range(5):
sess.run(train_step)
w_val = sess.run(w)
loss_val = sess.run(loss)
# 输出最后查看结果
print('{}\t{:.3f}\t{:.3f}'.format(i,w_val,loss_val))
将上面代码中train_step = tf.train.GradientDescentOptimizer(0.01).minimize(loss)的学习率分别改为1,0.1,0.01来观察程序的输出,将这个过程放在一个表格中,如下表所示:
通过观察上表可以发现,设置了3个不同的学习率来更新参数的值,如果参数的极优值是-1,如果将学习率设置为1,可以发现无论迭代多少次参数的值都在7和-5之间变化,永远也不可能达到-1。很显然,学习率设置为0.1还是比较合适的,更新速度相对于学习率设置为0.01而言更新速度不会太慢,而且迭代的次数也会少不少,最后的结果可能相差并不大。
所以说,学习率的设置还是非常重要的。其实,对于学习率的设置上面,我们可能会想着刚开始更新的时候,学习率尽可能的大,当参数快接近极优值的时候,学习率要变小,从而保证参数最后能够达到极优值而且保证迭代的次数足够小,减少资源的消耗,加快训练的速度。
tensorflow中常用学习率更新策略
分段常数衰减
分段常数衰减是在事先定义好的训练次数区间上,设置不同的学习率常数。刚开始学习率大一些,之后越来越小,区间的设置需要根据样本量调整,一般样本量越大区间间隔应该越小
tensorflow中定义了tf.train.piecewise_constant函数,实现了学习率的分段常数衰减功能。
tf.train.piecewise_constant(
x,#标量,指代训练次数
boundaries,#boundaries: 学习率参数应用区间列表
values,#学习率列表,values的长度比boundaries的长度多一个
name=None#操作的名称
)
示例代码
import matplotlib.pyplot as plt
import tensorflow as tf
def piecewise_constant_lr():
"""
分段常数衰减
:return:
"""
num_epoch= tf.Variable(0, name='global_step', trainable=False)
boundaries = [10, 20, 30]
learing_rates = [0.1, 0.07, 0.025, 0.12]
learing_rate = tf.train.piecewise_constant(num_epoch, boundaries=boundaries, values=learing_rates)
# 学习率正常情况下应该是衰减的,此处最后一个点添加了一个反常点,演示用
y = []
N = 40
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(N):
lr = sess.run([learing_rate],feed_dict={num_epoch:i})
y.append(lr)
x = range(N)
plt.plot(x, y, 'r-', linewidth=2)
plt.xlabel('epoch')
plt.ylabel('learn rate')
plt.title('piecewise_constant')
plt.grid(linestyle='-.')
plt.show()
if __name__ == '__main__':
piecewise_constant_lr()
前10个epoch采用0.1的学习率,第10~20epoch采用0.07的学习率,…,30个epoch后采用0.12的学习率。学习率曲线如下图所示:
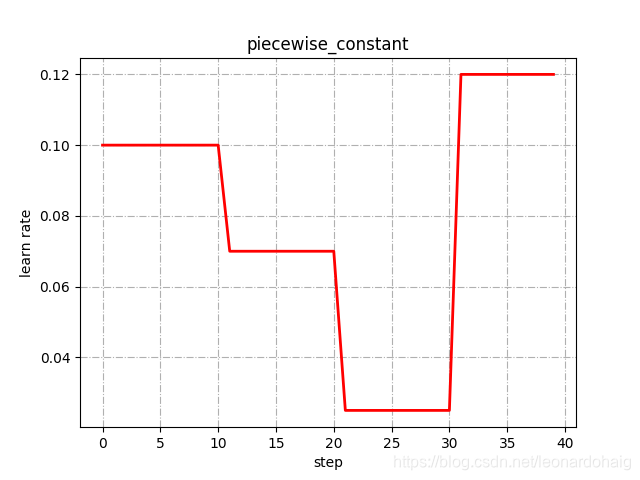
分段常数衰减可以让调试人员针对不同任务设置不同的学习率,进行精细调参,要求调试人员对模型和数据集有深刻认识,要求较高。
指数衰减
指数衰减是比较常用的衰减方法,学习率是跟当前的训练轮次指数相关的。
tf中实现指数衰减的函数是tf.train.exponential_decay()。
tf.train.exponential_decay(
learning_rate,#初始学习率
global_step,#当前训练轮次,epoch
decay_steps,#定义衰减周期,跟参数staircase配合,可以在decay_step个训练轮次内保持学习率不变
decay_rate,#衰减率系数
staircase=False,#定义是否是阶梯型衰减,还是连续衰减,默认是False,即连续衰减(标准的指数型衰减)
name=None#操作名称
)
函数返回学习率数值,计算公式是:
decayed_learning_rate =
learning_rate * decay_rate ^ (global_step / decay_steps)
代码如下:
def exponential_decay():
global_step = tf.Variable(0, name='global_step', trainable=False)
# 阶梯型衰减
learing_rate1 = tf.train.exponential_decay(
learning_rate=0.5,
global_step=global_step,
decay_steps=15,
decay_rate=0.9,
staircase=True)
# 标准指数型衰减
learing_rate2 = tf.train.exponential_decay(
learning_rate=0.5,
global_step=global_step,
decay_steps=15,
decay_rate=0.9,
staircase=False)
y = []
z = []
N = 500
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for num_epoch in range(N):
lr1 = sess.run([learing_rate1],feed_dict={global_step: num_epoch})
lr2 = sess.run([learing_rate2],feed_dict={global_step: num_epoch})
y.append(lr1)
z.append(lr2)
x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_ylim([0, 0.55])
# 支持中文
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['AR PL UKai CN'] # matplotlib中自带的中文字体
# 解决负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus'] = False
plt.plot(x, y, 'r', linewidth=2,linestyle = '-',label='阶梯型衰减')
plt.plot(x, z, 'g', linewidth=2,linestyle = ':',label='标准指数型衰减')
plt.title('exponential_decay')
plt.grid(linestyle='-.')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(loc='upper right')
plt.show()

红色的是阶梯型指数衰减,在一定轮次内学习率保持一致,绿色的是标准的指数衰减,即连续型指数衰减
自然指数衰减
自然指数衰减是指数衰减的一种特殊情况,学习率也是跟当前的训练轮次指数相关,只不过以自然常数e为底数。
tf中实现自然指数衰减的函数是tf.train.natural_exp_decay()。
tf.train.natural_exp_decay(
learning_rate,#初始学习率
global_step,#当前训练轮次,epoch
decay_steps,#定义衰减周期,跟参数staircase配合,可以在decay_step个训练轮次内保持学习率不变
decay_rate,#衰减率系数
staircase=False,#定义是否是阶梯型衰减,还是连续衰减,默认是False,即连续衰减(标准的指数型衰减)
name=None #操作名称
)
自然指数衰减的计算公式是:
decayed_learning_rate = learning_rate * exp(-decay_rate * global_step)
代码如下:
def natural_exp_decay():
global_step = tf.Variable(0, name='global_step', trainable=False)
y = []
z = []
w = []
m = []
N = 200
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
# 阶梯型衰减
learing_rate1 = tf.train.natural_exp_decay(
learning_rate=0.5,
global_step=global_step,
decay_steps=10,
decay_rate=0.9,
staircase=True)
# 标准指数型衰减
learing_rate2 = tf.train.natural_exp_decay(
learning_rate=0.5,
global_step=global_step,
decay_steps=10,
decay_rate=0.9,
staircase=False)
# 阶梯型指数衰减
learing_rate3 = tf.train.exponential_decay(
learning_rate=0.5,
global_step=global_step,
decay_steps=10,
decay_rate=0.9,
staircase=True)
# 标准指数衰减
learing_rate4 = tf.train.exponential_decay(
learning_rate=0.5,
global_step=global_step,
decay_steps=10,
decay_rate=0.9,
staircase=False)
for num_epoch in range(N):
lr1,lr2,lr3,lr4 = sess.run(
[learing_rate1,learing_rate2,learing_rate3,learing_rate4],
feed_dict={global_step: num_epoch})
y.append(lr1)
z.append(lr2)
w.append(lr3)
m.append(lr4)
x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_ylim([0, 0.55])
# 支持中文
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['AR PL UKai CN'] # matplotlib中自带的中文字体
# 解决负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus'] = False
plt.plot(x, y, 'r-', linewidth=2, label='自然指数阶梯型衰减')
plt.plot(x, z, 'g-', linewidth=2, label='自然指数标准型衰减')
plt.plot(x, w, 'r', linewidth=1, linestyle = '-.', label='阶梯型衰减')
plt.plot(x, m, 'g', linewidth=1, linestyle = '-.', label='标准指数型衰减')
plt.title('natural_exp_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.grid(linestyle='-.')
plt.legend(loc='upper right')
plt.show()
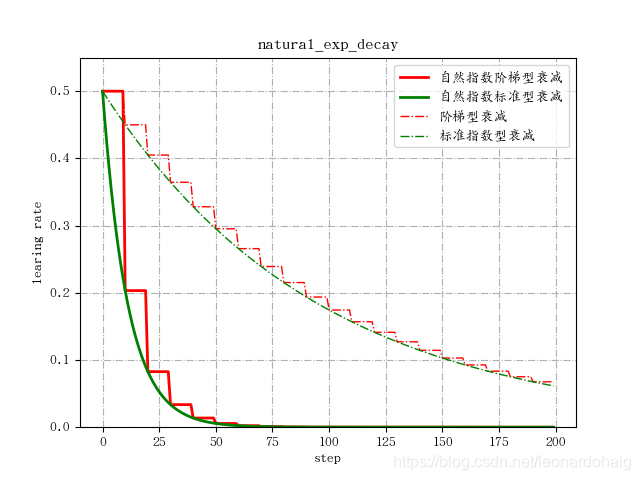
左下部分的两条曲线是自然指数衰减,右上部分的两条曲线是指数衰减,可见自然指数衰减对学习率的衰减程度要远大于一般的指数衰减,一般用于可以较快收敛的网络,或者是训练数据集比较大的场合。
多项式衰减
多项式衰减是这样一种衰减机制:定义一个初始的学习率,一个最低的学习率,按照设置的衰减规则,学习率从初始学习率逐渐降低到最低的学习率,并且可以定义学习率降低到最低的学习率之后,是一直保持使用这个最低的学习率,还是到达最低的学习率之后再升高学习率到一定值,然后再降低到最低的学习率(反复这个过程)。
tf中实现多项式衰减的函数是tf.train.polynomial_decay()。
tf.train.polynomial_decay(
learning_rate,#初始学习率
global_step,#当前训练轮次,epoch
decay_steps,#定义衰减周期
end_learning_rate=0.0001,#最小的学习率,默认值是0.0001
power=1.0,#多项式的幂,默认值是1,即线性的
cycle=False,#定义学习率是否到达最低学习率后升高,然后再降低,默认False,保持最低学习率
name=None #操作名称
)
多项式衰减的学习率计算公式:
global_step = min(global_step, decay_steps)
decayed_learning_rate = (learning_rate - end_learning_rate) *
(1 - global_step / decay_steps) ^ (power) +
end_learning_rate
如果定义cycle=True,学习率在到达最低学习率后往复升高降低,此时学习率计算公式为:
decay_steps = decay_steps * ceil(global_step / decay_steps)
decayed_learning_rate = (learning_rate - end_learning_rate) *
(1 - global_step / decay_steps) ^ (power) +
end_learning_rate
代码如下:
def polynomial_decay():
global_step = tf.Variable(0, name='global_step', trainable=False)
# cycle=False
learing_rate1 = tf.train.polynomial_decay(
learning_rate=0.1, global_step=global_step, decay_steps=50,
end_learning_rate=0.01, power=0.5, cycle=False)
# cycle=True
learing_rate2 = tf.train.polynomial_decay(
learning_rate=0.1, global_step=global_step, decay_steps=50,
end_learning_rate=0.01, power=0.5, cycle=True)
y = []
z = []
N = 200
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for num_epoch in range(N):
lr1, lr2 = sess.run([learing_rate1, learing_rate2],feed_dict={global_step: num_epoch})
y.append(lr1)
z.append(lr2)
x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, z, 'g-', linewidth=2, label='cycle=False')
plt.plot(x, y, 'r--', linewidth=2, label='cycle=True')
plt.title('polynomial_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.grid(linestyle='-.')
plt.legend(loc='upper right')
plt.show()
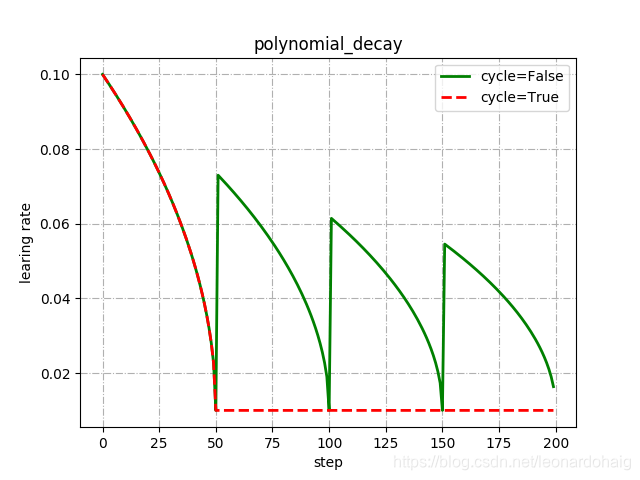
红色的学习率衰减曲线对应 cycle = False,下降后不再上升,保持不变,绿色的学习率衰减曲线对应 cycle = True,下降后往复升降。
多项式衰减中设置学习率可以往复升降的目的是为了防止神经网络后期训练的学习率过小,导致网络参数陷入某个局部最优解出不来,设置学习率升高机制,有可能使网络跳出局部最优解。
余弦衰减
余弦衰减的衰减机制跟余弦函数相关,形状也大体上是余弦形状。tf中的实现函数是:tf.train.cosine_decay()
tf.train.cosine_decay(
learning_rate,#初始学习率
global_step,#当前训练轮次,epoch
decay_steps,# 衰减步数,即从初始学习率衰减到最小学习率需要的训练轮次
alpha=0.0,#最小学习率
name=None #操作的名称
)
余弦衰减学习率计算公式:
global_step = min(global_step, decay_steps)
cosine_decay = 0.5 * (1 + cos(pi * global_step / decay_steps))
decayed = (1 - alpha) * cosine_decay + alpha
decayed_learning_rate = learning_rate * decayed
改进的余弦衰减方法还有:
- 线性余弦衰减,对应函数
tf.train.linear_cosine_decay() - 噪声线性余弦衰减,对应函数
tf.train.noisy_linear_cosine_decay()
代码如下:
def cosine_decay():
global_step = tf.Variable(0, name='global_step', trainable=False)
# 余弦衰减
learing_rate1 = tf.train.cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=50)
# 线性余弦衰减
learing_rate2 = tf.train.linear_cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=50,
num_periods=0.2, alpha=0.5, beta=0.2)
# 噪声线性余弦衰减
learing_rate3 = tf.train.noisy_linear_cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=50,
initial_variance=0.01, variance_decay=0.1, num_periods=0.2, alpha=0.5, beta=0.2)
y = []
z = []
w = []
N = 200
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for num_epoch in range(N):
lr1, lr2, lr3 = sess.run(
[learing_rate1, learing_rate2, learing_rate3],
feed_dict={global_step: num_epoch})
y.append(lr1)
z.append(lr2)
w.append(lr3)
# 支持中文
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['AR PL UKai CN'] # matplotlib中自带的中文字体
# 解决负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus'] = False
x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, z, 'fuchsia', linewidth=2, label='线性余弦衰减')
plt.plot(x, y, 'r-', linewidth=2, label='余弦衰减')
plt.plot(x, w, 'skyblue', linewidth=2, label='噪声线性余弦衰减')
plt.title('cosine_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.grid(linestyle='-.')
plt.legend(loc='upper right')
plt.show()
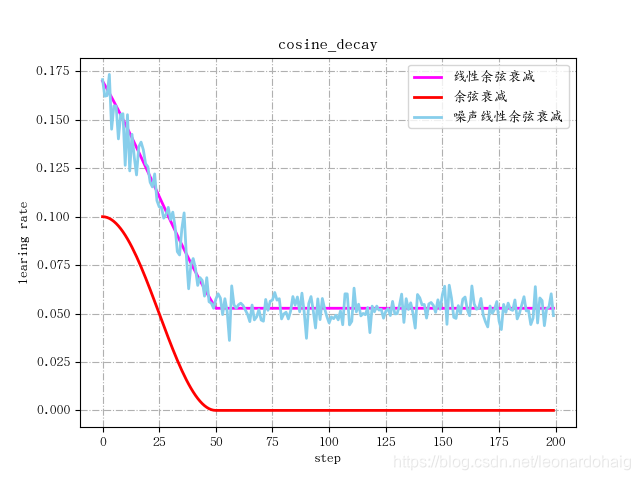
- 标准余弦衰减,学习率从初始曲线过渡到最低学习率;
- 线性余弦衰减,学习率从初始线性过渡到最低学习率;
- 噪声线性余弦衰减,在线性余弦衰减基础上增加了随机噪声;
倒数衰减
倒数衰减指的是一个变量的大小与另一个变量的大小成反比的关系,具体到神经网络中就是学习率的大小跟训练次数有一定的反比关系。
tf中实现倒数衰减的函数是 tf.train.inverse_time_decay()。
tf.train.inverse_time_decay(
learning_rate,#初始学习率
global_step,#用于衰减计算的全局步数
decay_steps,#衰减步数
decay_rate,#衰减率
staircase=False,#是否应用离散阶梯型衰减(否则为连续型)
name=None #
)
代码如下:
def inverse_time_decay():
global_step = tf.Variable(0, name='global_step', trainable=False)
# 阶梯型衰减
learing_rate1 = tf.train.inverse_time_decay(
learning_rate=0.1, global_step=global_step, decay_steps=20,
decay_rate=0.2, staircase=True)
# 连续型衰减
learing_rate2 = tf.train.inverse_time_decay(
learning_rate=0.1, global_step=global_step, decay_steps=20,
decay_rate=0.2, staircase=False)
y = []
z = []
N = 200
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for num_epoch in range(N):
lr1, lr2 = sess.run([learing_rate1, learing_rate2],
feed_dict={global_step: num_epoch})
y.append(lr1)
z.append(lr2)
# 支持中文
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['AR PL UKai CN'] # matplotlib中自带的中文字体
# 解决负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus'] = False
x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, z, 'r-', linewidth=2, label='阶梯型衰减')
plt.plot(x, y, 'g-', linewidth=2, label='连续型衰减')
plt.title('inverse_time_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.grid(linestyle='-.')
plt.legend(loc='upper right')
plt.show()
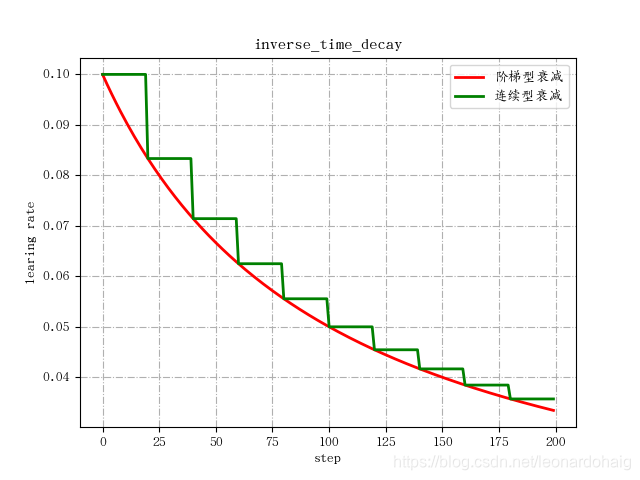
倒数衰减不固定最小学习率,迭代次数越多,学习率越小。
参考资料
1.TensorFlow优化模型之学习率的设置
2.tensorflow笔记__学习率的设置
3.tensorflow中常用学习率更新策略























 1320
1320

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








