1. 二叉排序树的案例引入
1.1. 需求
给定数列 arr = {7,3,10,12,5,1,9},
要求能高效的完成对数据的查询和添加.
1.2. 分析
- 使用数组
- 数组未排序
- 优点: 直接在数组尾部添加, 速度快
- 缺点: 查找元素的速度慢
- 数组已排序
- 优点: 可以使用二分查找, 查找速度快
- 缺点: 为保证数组有序, 插入新数据都要重新排序,
每次排序都要使数据插入位后的数据整体后移, 速度慢
- 使用链式存储-链表
优点: 添加数据速度比数组快, 不需要数据整体移动.
缺点: 不管链表是否有序, 查找速度都慢.
- 使用二叉排序树
下面开始进行介绍
2. 二叉排序树(BST)的原理
2.1. 基本介绍
-
二叉排序树 Binary Sort(Search) Tree, 简称 BST.
-
对于二叉排序树的任何一个非叶子结点而言,
要求左子结点的值比父结点的值小, 右子结点的值比父结点的值大.
如果子结点的值和父结点相同, 可以左右任意放置该子结点. -
针对前面需求所给出的数组
arr = {7,3,10,12,5,1,9}- 对应的二叉排序树如下图所示:
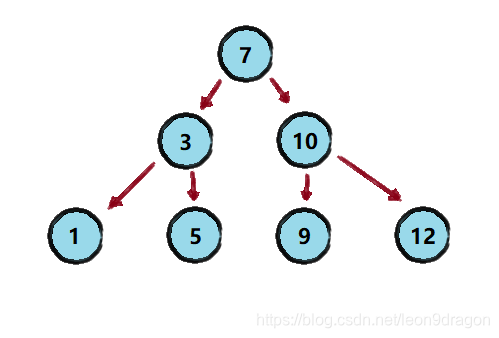
- 插入一个结点 2 后的图示:
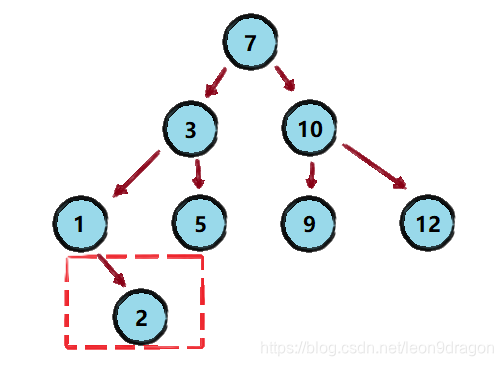
- 对应的二叉排序树如下图所示:
3. 二叉排序树的创建和遍历
3.1. 思路分析
- 插入新的结点的时候与调用插入方法的结点进行比较
- 如果小于等于调用结点, 则向左进行
- 若调用方法的结点的左子结点为空, 则直接将新结点挂上去即可
- 若调用方法的结点的左子结点非空, 则利用其左子结点调用方法
- 如果大于调用结点, 则向右进行
- 若调用方法的结点的右子结点为空, 则直接将新结点挂上去即可
- 若调用方法的结点的右子结点非空, 则利用其右子结点调用方法
- 如果小于等于调用结点, 则向左进行
3.2. 代码实现
3.2.1. 结点类
package com.leo9.dc28.binary_sort_tree;
public class TreeNode {
public int value;
public TreeNode left_node;
public TreeNode right_node;
public TreeNode(int value) {
this.value = value;
}
//region 添加结点的方法
//递归形式添加结点, 注意需要满足二叉排序树的要求
public void addNode(TreeNode new_node) {
//若传入空结点则直接返回即可
if (new_node == null) {
return;
}
//region 判断传入的结点的值, 和当前调用方法的结点的值关系
//如果新结点的值小于等于当前调用结点的值
if (new_node.value <= this.value) {
//如果当前调用结点的左子结点为空, 则直接将新结点接在其左子结点即可
if (this.left_node == null) {
this.left_node = new_node;
}
//如果不为空, 递归向左添加
else {
this.left_node.addNode(new_node);
}
}
//如果新结点的值大于当前调用结点的值
else {
//如果当前调用结点的右子结点为空, 则直接将新结点接在其右子结点即可
if (this.right_node == null) {
this.right_node = new_node;
}
//如果不为空, 递归向右添加
else {
this




 本文详细介绍了如何使用二叉排序树解决数据快速查询与添加问题,包括二叉树的原理、创建与遍历方法,以及复杂删除操作的思路和代码实现。通过实例演示了删除叶子节点、单子树和双子树的情况。
本文详细介绍了如何使用二叉排序树解决数据快速查询与添加问题,包括二叉树的原理、创建与遍历方法,以及复杂删除操作的思路和代码实现。通过实例演示了删除叶子节点、单子树和双子树的情况。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2330
2330

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








