LeetCode每日一题（2020.10.15） 507. 完美数

LeetCode每日一题（2020.10.15）

最难做的事，就是把容易做的事持之以恒。

今日题目：

507. 完美数

        难度：简单

对于一个 正整数，如果它和除了它自身以外的所有 正因子 之和相等，我们称它为 「完美数」。

给定一个 整数 n， 如果是完美数，返回 true，否则返回 false

示例 1：

输入：28
输出：True
解释：28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, 和 14 是 28 的所有正因子。

示例 2：

输入：num = 2
输出：false

提示：

1 <= num <= 10^8

通过次数18,795，提交次数48,770

首先，给出我自己写的代码：

class Solution:
    def checkPerfectNumber(self, num: int) -> bool:
        sum=0
        n=num//2+1
        if num>5 :
            for i in range(1,n):
                if num/i==num//i:
                    sum+=i
            if(sum==num):
                return True
            else:
                return False
        else:
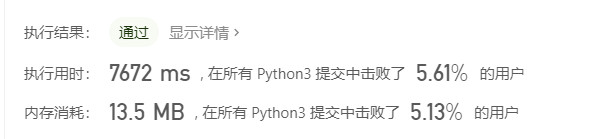
            return False

很简单，不需要过多的解释也能看得懂。需要注意的是，为什么n=num//2+1，需要+1，因为range()方法是顾首不顾尾，即range(2,10)，生成的序列只有2-9，不包含10。所以n必须要+1才能实现1-n的序列，这是比较容易遗漏的点。当然我自己写的这个方法确实不怎么样，执行时间和内存消耗都很差，下面借鉴一下LeetCode上面大神的方法。

优化算法一：

class Solution:
    import math
    def checkPerfectNumber(self, num: int) -> bool:
        sum=1
        n=int(math.sqrt(num))+1
        if num>5:
            for i in range(2,n):
                if num/i==num//i:
                    sum+=i + num/i
            if(sum==num):
                return True
            else:
                return False
        else:
            return False

在我自己写的算法里面，for循环的次数是n=num//2+1，次数还是太多了，循环次数可以优化为n=sqrt(num)+1，以为num的两个因子必然一个分布在[1,sqrt(num)]，另一个分布在[sqrt(num),num]，我们只需要在找出第一个因子的时候，把第一个因子对应的第二个因子也加到sum中，就可以简化循环次数，以优化算法执行时间。

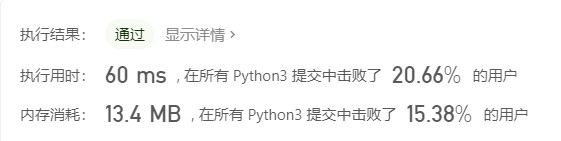
再看一下优化后的算法的执行时间和内存占用，可以发现，运行时间确实少了很多，从7672ms减少到了60ms，由此可见，我们在写for循环的时候，应该尽量减少循环的次数，以提高程序运行时间。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/perfect-number
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。