排序算法总结｜基本思路

本文参考bobo老师的教学视频。

O(n^2)的算法

1. 选择排序

每次选最小的元素，放到前面排序部分的最后一个位置

 

2. 插入排序

每次从未排序部分取第一个元素，不断向前面排好序里的元素比大小+交换，直到插入合适位置

缺点：频繁交换位置，交换操作耗时

改进：前面排序部分后移，直到找到合适位置再将元素放入

优点：在近乎有序的时候，插入效果近似O(n)

 

3. 希尔排序（插入的改进）

出发点：插入在近乎有序的时候很快，所以希尔先在大跨度上排序，然后逐渐减小步长

 

4. 冒泡排序

 

 

O(nlogn)的算法

1. 归并排序

自定向上：从上到下分割，然后排序

自底向上：初始每2个元素一组排序，接着4个…

对比：

1）递归自顶向下稍快一些

2）自底向上适合用于链表（因为不需要直接访问）

 

2. 快速排序

2种思路：

1）前面记录小于key的元素，中间记录大于key，后面是未遍历的。

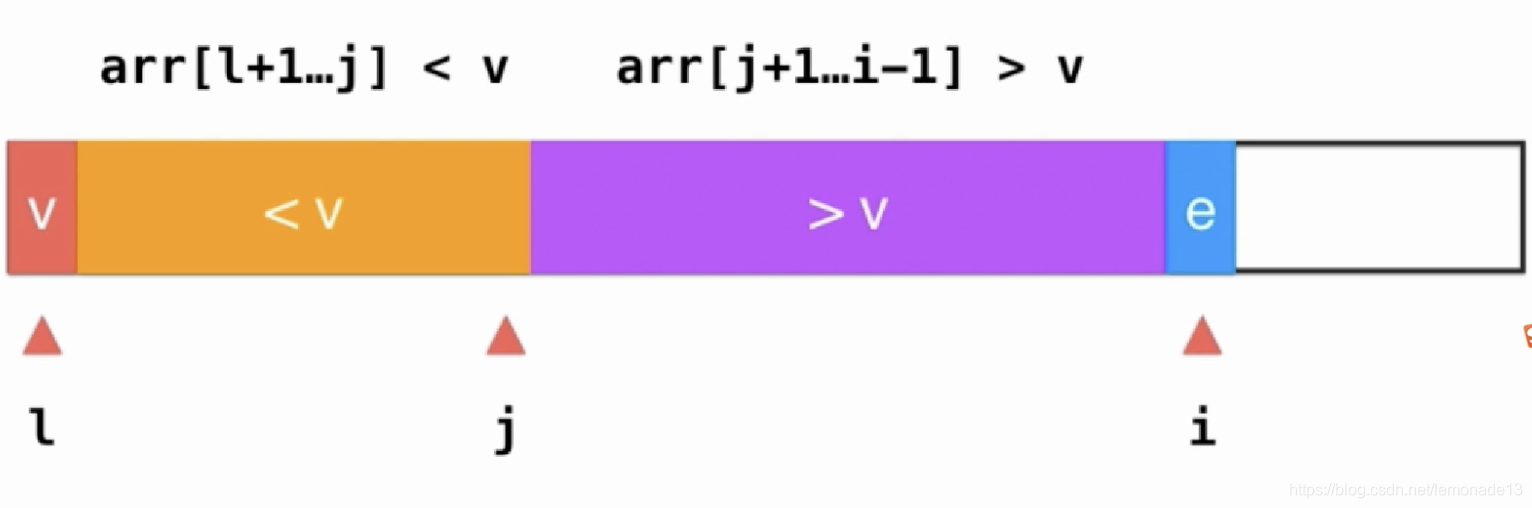
✅2）头尾两个指针，不断判断是否位置交换。

对于思路1）的讨论

优化1:在底层（长度小）时用插入排序优化

缺点2:近乎有序情况很慢，最差退化为O(n^2)，树变成链表

优化2:随机选择key，把取到的key暂存到开头

缺点3:数列中存在大量重复值，key去到了重复值，退化成O(n^2)

优化3:使用头尾指针方式

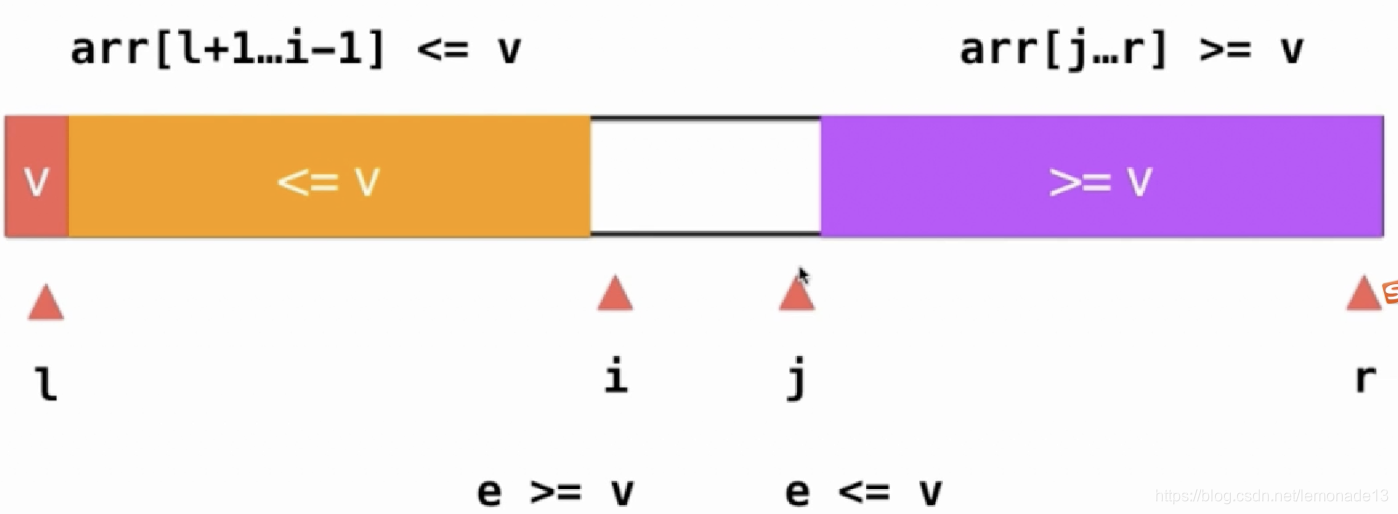
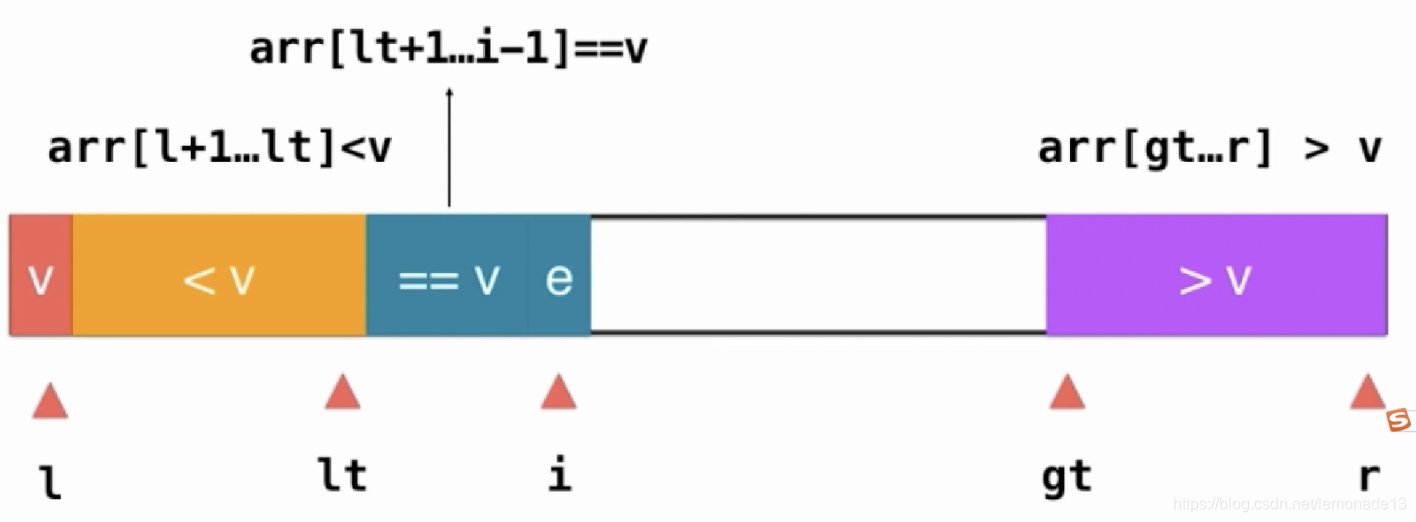
优化4:三路快排，数列分为 <key =key >key的三部分

 

 

分治算法 的题目

归并和快排都是分治思想

 

1）求数列中逆序对数量

使用归并在merge部分的思想，O(nlogn)

 

2）取无序数组第k大值

法一：快排的partition思想， O(n)=n+n/2+n/4+n/8+…

法二：维护k大小的大顶堆

 

6. 堆排序

1）优先队列

 

二叉堆：完全二叉树，父节点总是大于孩子。

（注意：不一定层越高 值越大）

 

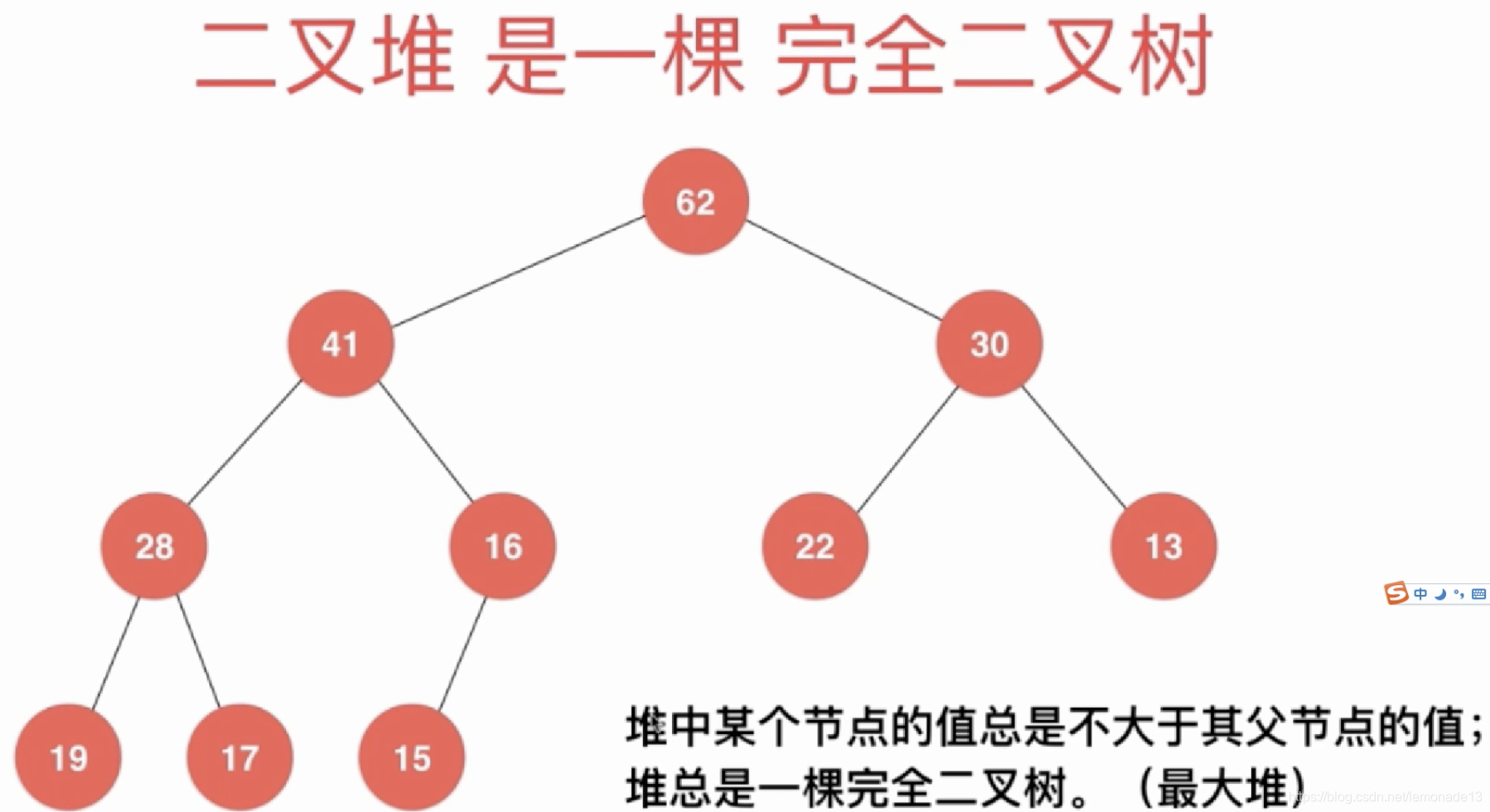
实现：数组（完全树索引可以），从下标1开始存储

添加元素：添加在末尾，不断和父节点比较，更大则把父亲换下来

取元素：出根节点，把最后一个元素放到根，然后不断向较大的孩子比较交换

（优化：先多次比较，只做一次交换操作）

 

创建堆：

法1:数组转为堆 Heapify：每个叶子节点都看作一个最大堆，每个叶子依次做向上比较交换，不断扩大满足最大堆性质的范围，复杂度O(n)

法2:不断insert：复杂度O(nlogn)

 

原地堆排序：直接将下标从0开始的数组转为堆

 

2）索引堆

普通堆的问题：如果元素复杂，如文章字符串、进程，交换元素位置就很慢

索引堆：数据和索引分开存储

 

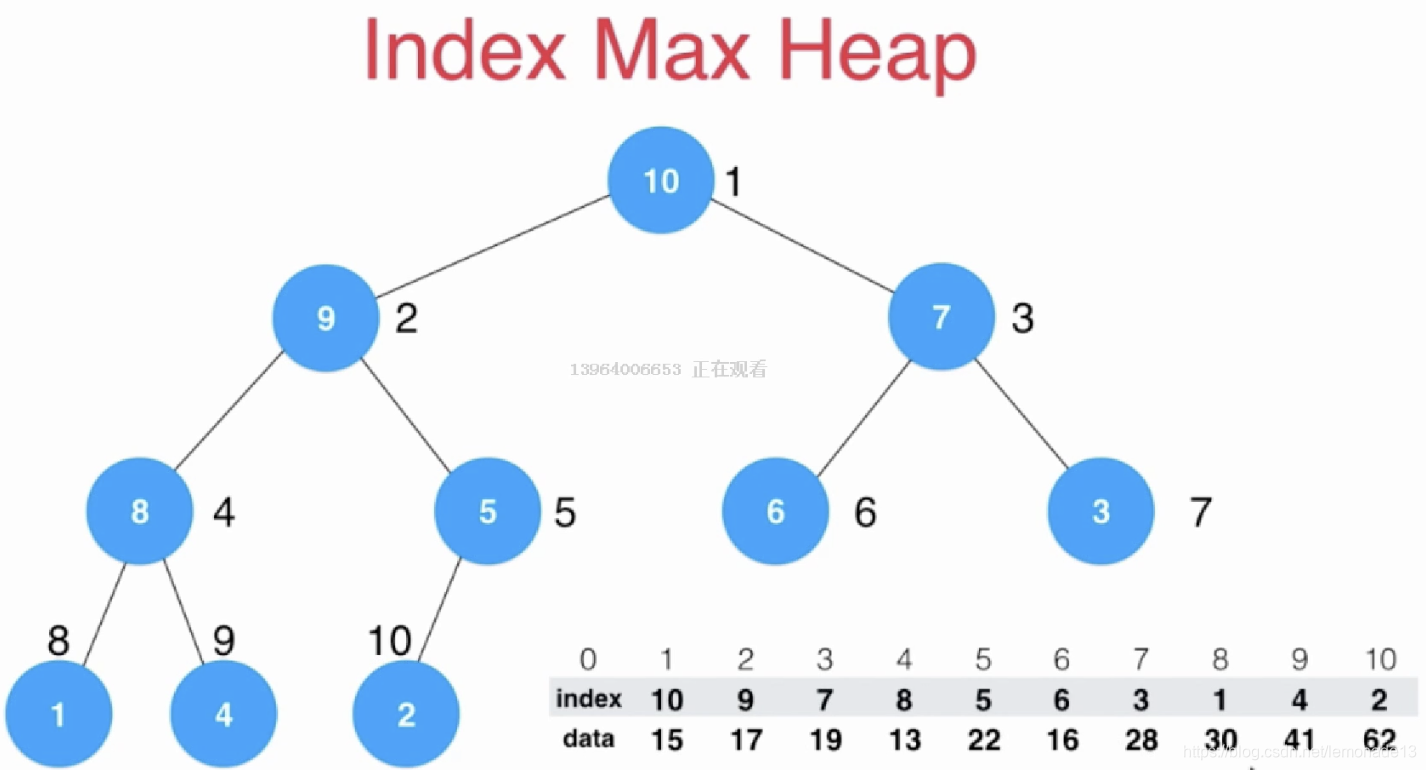
问题：由数据 找索引 找堆中的位置

优化：

空间            下标                 元素                含义

index    堆中位置                索引            堆中位置存的索引

data           索引                 数据            索引对应的数据

reverse      索引                堆中位置       索引在堆中位置

 

 

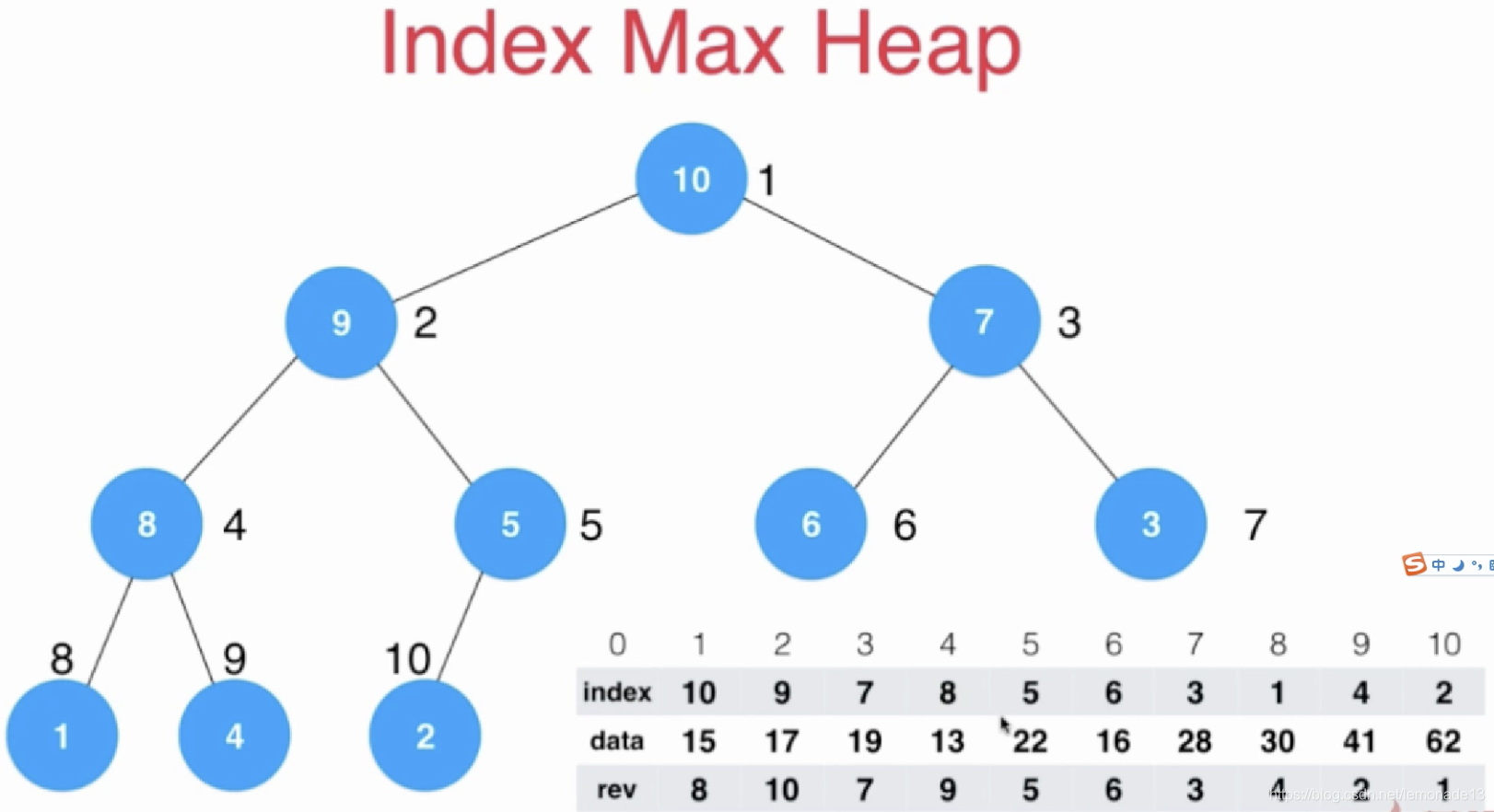
堆排序 的问题

1）第k大元素

2）多路归并排序

 

 

总结排序算法

快排比其他相同复杂度的排序算法有常数级别的快。

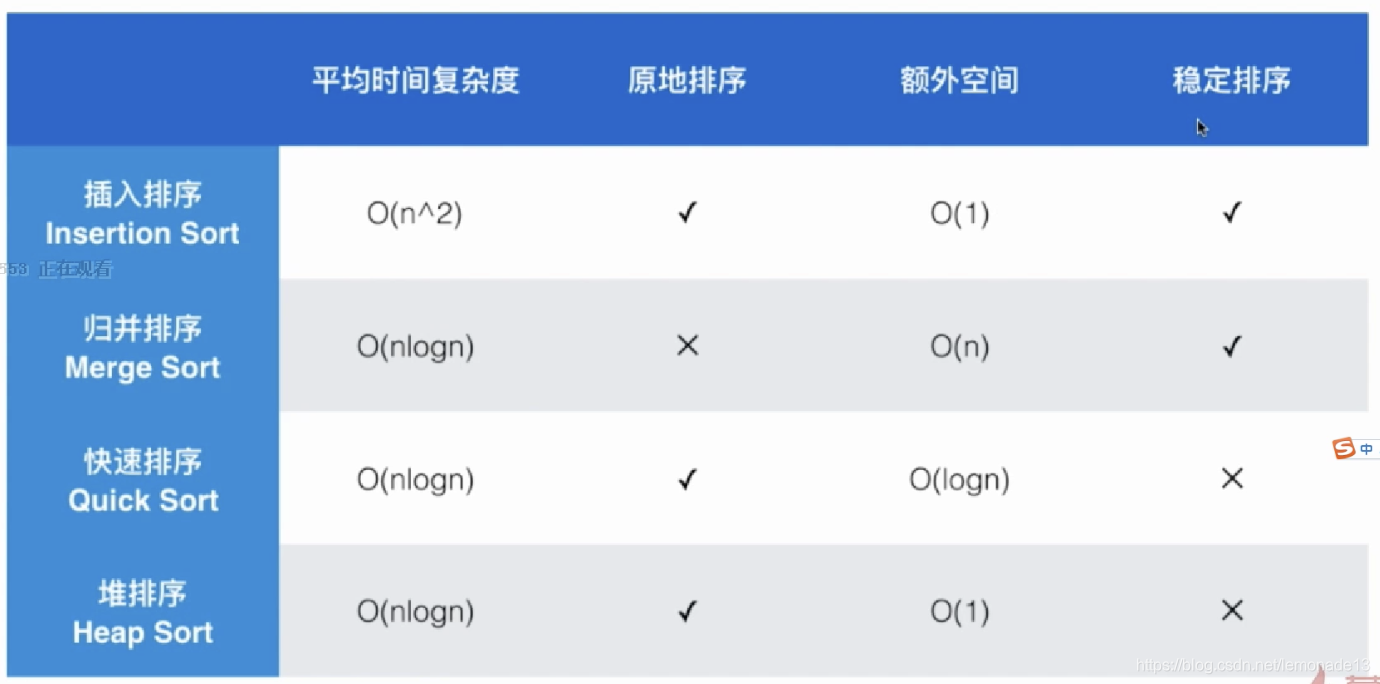
快排额外空间在于递归。