微分方程
1.结论对于二阶齐次线性微分方程,若 y1(x)和 y2(x)是两个线性无关的解,则通解为 y=C1y1(x)+C2y2(x)。二阶齐次线性微分方程的通解结构是:如果 y1和 y2是两个线性无关的解,那么通解是它们的线性组合 y=C1y1+C2y2
2.定义简单说,微分方程就是含有未知函数及其导数的等式
3.结论(2x−1)w′+(2x−3)w=0这是可分离变量的一阶微分方程类似形式
4.方法降阶法的思想:用已知解构造新解,把高阶方程降成低阶,逐步求解
5.方法利用初始条件 u(−1)=e和 u(0)=−1确定 u(x)的具体表达式
6.结论 e−x⋅ex=1
7.结论显然,左边是指数增长,右边是线性函数,不可能相等,所以它们线性无关
8.结论u=2x−1(求导后变简单),则 du=2dx
9.
关键字的比较次数
1.结论满二叉树深度为3节点必为7
2.结论对于长度为 n的有序表,折半查找判定树的深度 h满足不等式:2h−1−1<n≤2h−1当 h=5时,25−1−1=15,25−1=31→ 16落在 [15,31]区间内,因此判定树深度 h=5
递归方式对顺序表进行快速排序
摄影
比较定积分大小
线性探测法 中的 查找成功 和 查找失败 的平均查找长度(ASL)的计算方法
旋转体体积和表面积
1.
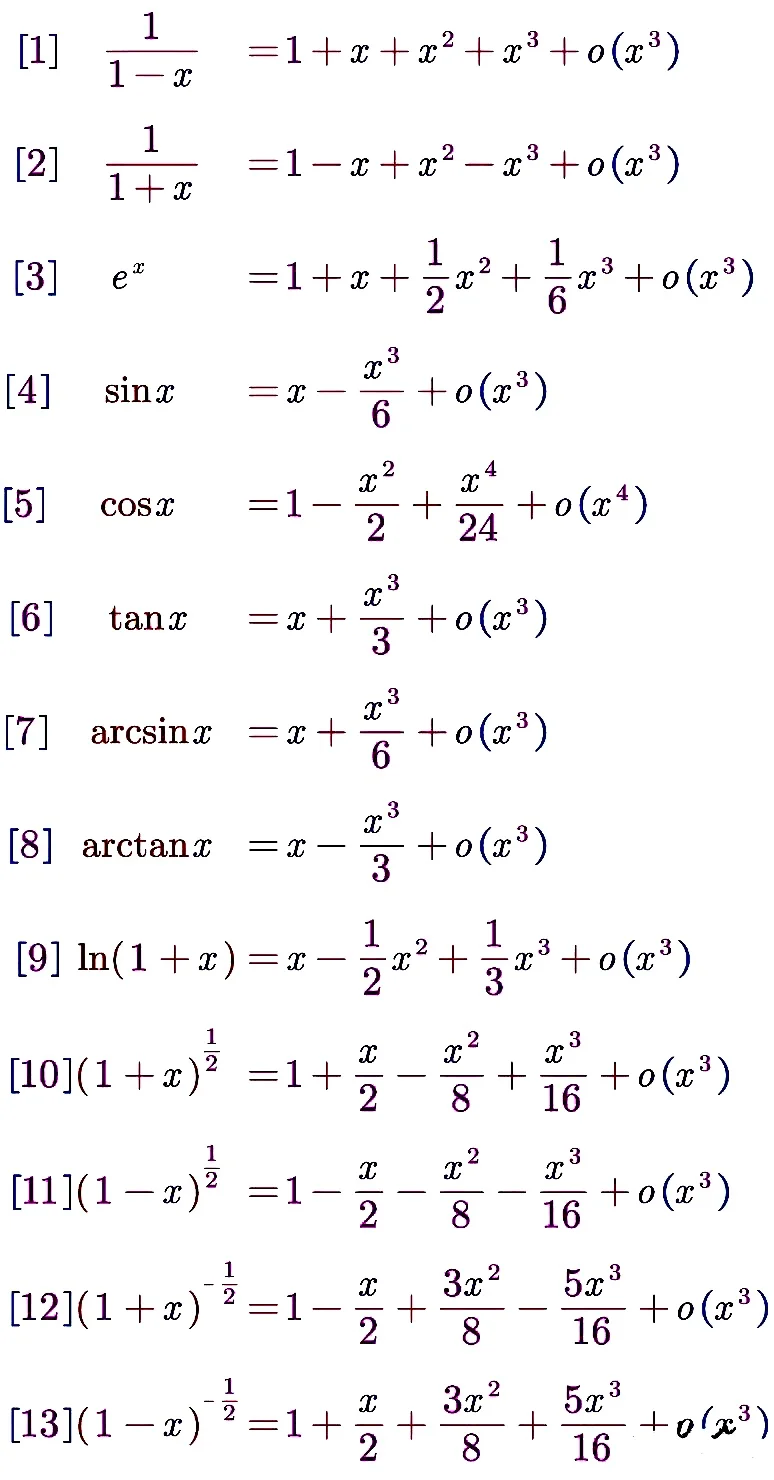






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








