本文深入探讨了链表的各种高级操作，包括双向链表的反转、判断链表是否为回文链表、链表双指针问题的应用、删除链表中的重复节点、删除单链表中的指定节点、链表分割、链表求和以及检测链表环等问题。并提供了详细的算法思路和代码实现。
链表的扩展操作21：
(1)双向链表反转
(2)链表是否为回文链表
(3)链表双指针问题
(4)删除链表中的重复节点
(5)删除单链表中的某个节点
(6)以x为基准将链表分为两个部分,小于x在前，大于x在后
(7)通过链表求两个数字之和
(8)给定一个有环的链表，返回链表环的开头节点
(9)单链表在O(1)删除指定的节点
----------------
（一）反转
(1)单链表的反转
略
(1)双链表的反转
struct ListNode
{
ListNode* pre;
int data;
ListNode* next;
};
现要实现输入一个双向链表头指针，反转链表，并返回反转后的头指针。链表节点如下图，关键代码如下：
分析：其实我觉得双向链表的反转完全没有必要，如果非要反转，就更新下头指针以及尾指针。将头指针指向之前的尾部。
然后将尾指针，指向之前的头部即可；
ListNode* reverse(ListNode* head)
{
if(head==NULL || head->next==NULL)
{
return head;
}
ListNode *pnode=head,*pre=NULL; //pnode指向当前节点，pre指向前一节点
while (pnode) //当pnode！=null时，开始反转
{
ListNode* pnext=pnode->next;
//首先保存pnode的下一节点保存到pnext，否则反转（1）链时会丢失下一节点指向。
pnode->next=pre;
//反转（1）链，指向前一节点，当pnode为头节点时，pre指针为空。
pnode->pre=pnext;
//反转（2）链，指向下一节点，当pnode为尾节点时，pnext指针为空。
pre=pnode; //反转完成，后移pre指针。
pnode=pnext; //后移pnode指针。
}
return pre; //当pnode为Null时，说明已经反转完毕，它的前一节点pre指向尾节点。返回此节点指针。
}
--------------
（二）判断链表是否为回文链表
注：如何能达到时间复杂度为O(n)的同时空间复杂度为O(1)；
（1）分析
（1.1）思路一
- 遍历链表,用数组存下每个节点的值,然后从数组两头开始向中间遍历,是否相等
- 时间复杂度O(n),空间复杂度O(n)
（1.2）思路二
利用栈先进后出的性质，将链表前半段压入栈中，再逐个弹出与链表后半段比较。时间复杂度O（n），但仍然需要n/2的栈空间，空间复杂度为O（n）。
（1.3）思路三
- 遍历一遍链表,得到链表长度n,根据长度的奇偶,找到中间节点,将左半边的链表反转,然后从中间节点分两个方向向左右两边遍历,是否是回文;
- 最后对左半部分链表进行反转,还原为最初的链表
- 只需要固定的若干个临时变量,不需要额外开辟空间
- 时间复杂度为O(n),空间复杂度为O(1)
（2）实现
// ListNode Definition for singly-linked list.
type ListNode struct {
Val int
Next *ListNode
}
// 解法1
// 用数组存前面的一半节点的值
// 时间复杂度：O(N)
// 空间复杂度：O(N)
func isPalindrome(head *ListNode) bool {
// 空链表,算回文
if head == nil {
return true
}
var data []int
for cur := head; cur != nil; cur = cur.Next {
data = append(data, cur.Val)
}
for i, j := 0, len(data)-1; i <= j; {
if data[i] != data[j] {
return false
}
i++
j--
}
return true
}
// 解法2
// 找到链表中间节点，将前半部分转置，再从中间向左右遍历对比
// 时间复杂度：O(N)
// 空间复杂度：O(1)
func isPalindrome2(head *ListNode) bool {
if head == nil || head.Next == nil {
return true
}
isPalindrome := true
//链表长度
length := 0
for cur := head; cur != nil; cur = cur.Next {
length++
}
//将前半部分反转
step := length / 2
var prev *ListNode
cur := head
for i := 1; i <= step; i++ {
cur.Next, prev, cur = prev, cur, cur.Next
}
mid := cur
var left, right *ListNode = prev, nil
if length%2 == 0 {
//长度为偶数
right = mid
} else {
right = mid.Next
}
//从中间向左右两边遍历对比
for left != nil && right != nil {
if left.Val != right.Val {
//值不相等,不是回文链表
isPalindrome = false
break
}
left = left.Next
right = right.Next
}
//将前半部分反转的链表进行复原
cur = prev
prev = mid
for cur != nil {
cur.Next, prev, cur = prev, cur, cur.Next
}
return isPalindrome
}
c语言实现如下：
判断链表是否有环”思想利用快慢指针法找到链表中点，然后一个将后半部分就地反转，分别再从头、中点遍历判断是否相等，该方法时间复杂度O(n)、空间复杂度O(1).
bool isParadom(ListNode * head)
{
//如果链表为空或者仅有一个元素那么肯定是回文链表
if (!head || !head->next) {
return true;
}
//快慢指针法，寻找链表中心
ListNode * slow, *fast;
slow = fast = head;
while (fast && fast->next) {
/* fast跳跃2步，所以需要判断当前fast是否为空，以及fast下一步是否为空；
如果当前fast为空，则取fast下一步出错；
如果fast下一步为空，则取fast下2步出错；
*/
slow = slow->next;
fast = fast->next->next;
}
if (fast) {
// 最简单的只有3个节点 aba，则循环结束时 fast->next == null;
// 链表元素奇数个；fast非空，则上诉循环结束条件为 fast->next为空;
// 此时slow的位置就是中间节点的位置，即b的位置；奇数个节点时，需要将中间节点的右边的节点给反转了。
slow->next = reverseList(slow->next);
slow = slow->next;
}
else {
//最简单的只有4个节点 abba，则循环结束时 fast == null;
//链表元素偶数个；
// 此时slow的位置为 偏向右边的中间节点即第二个b的位置，此时需要将以ta为头结点的链表进行反转；
slow = reverseList(slow);
}
while (slow) {
if (head->val != slow->val) {
return false;
}
slow = slow->next;
head = head->next;
}
return true;
}
ps: 字符串或者数组的回文问题： 略
---------------
（三）链表双指针问题
（1）定义：
指的是用两个指针来迭代访问链表。
（2）范例：
1.求取链表中倒数第k个节点。
2.求取链表中的中间节点。（快慢双指针）
3.判断链表是否有环（快慢双指针）以及环的入口处。
4.假设有一个链表a1->a2->...->an->b1->b2->..->bn，将其重新排列为a1->b1->a2->b2->...->an->bn(即完美洗牌问题)；
解决方法：
1)定义两个指针p1，p2，p1每次走两步，p2每次走一步，
2)当p1到达链表末尾时，p2刚好到达中间位置。（当p1=null时，p2=b1）.
3)然后p3从头开始，每次走一步，将p2所指的节点放到p3后面。
-----------
（四）删除链表中的重复节点：
（1）使用HashTable;
时间复杂度为O(N),空间复杂度为O(N)
void deleteRepeat(LinkNode* head){
HashTable<DataType , bool> table=new HashTable<DataType , bool>();
LinkNode* pre=head;
LinkNode* cur=head->next;
while(cur!=NULL){
if(table.containKey(cur->data)){
pre->next=cur->next;
}else{
table.put(cur->data,true);
pre=cur;
}
cur=cur->next;
}
}
（2）不使用缓冲区：
时间复杂度为O(n^2),空间复杂度为O(1);
1）分析：使用两个指针，cur迭代扫描整个链表，runner用于扫描后续的节点是否重复。
void deleteRepeat(LinkNode* head){
if(NULL==head || NULL==head->next)
return ;
LinkNode* cur=head->next;
while(cur!=NULL){
LinkNode* runner=cur;
while(runner->next){
if(runner->next->data==cur->data){
runner->next=runner->next->next;//删除runner->next;
}else{
runner=runner->next;
}
}
cur=cur->next;
}
}
--------
（五）删除单链表中的某个节点，假定只能访问该待删除节点，不能访问首节点。
1）分析：
直接将后继节点的数据复制到当前节点，然后删除后继节点。
2）实现：
bool deleteNode(Node* pnode){
if(NULL==pnode || NULL==pnode->next)
return false;
Node* pnext=pnode->next;
pnode->data=pnext->data;
pnode->next=pnext->next;
delete pnext;
return true;
}
--------
（六）以x为基准将链表分为两个部分，所有小于x的节点排在大于或等于x的节点之前。
1）分析：类似于数组的快速排序。但是此中是链表，不需要移动数据，更容易实现。
2）方法：
1.创建两个链表，一个链表存放小于x的节点，另一个链表存储大于等于x的节点。
2.迭代访问整个链表，将元素插入到before或after链表中，一旦抵达链表的末端，则表明拆分完成，最后合并两个链表。
------
（七）给定两个用链表表示的整数，每个节点表示一个数位，这些数位是反向的，即个位排在链表的首部。编写函数对两个整数求和。最终的和仍然存储在链表中，且为反向存储。
（1）分析：结合加法的对齐方式，以及链表的访问必须从头到尾访问，反向存储是较为简单的方法。
（2）实现：
/*
根据当前list1->data，list2->data,以及carry，
返回一个data=(list1->data+list2->data+crray)%10的节点
*/
LinkNode* addLists(LinkNode* list1,LinkNode* list2,int carry ){
if(list1==NULL && list2==NULL && carray==0)
return NULL;
linkNode* result=new LinkNode();
int sum=carry;
if(list1){
sum+=list1->data;
}
if(list2){
sum+=list2->data;
}
result->data=sum%10;
LinkNode* pnode=addLists(list1==NULL?NULL:
list1->next,list2==NULL?NULL:
list2->next2,value>10?1:0);
result->next=pnode;
result=pnode;
return result;
}
注意：此中注意的是处理两个链表长度不一样时。
（3）进阶：
当这些数位都是正序存放的，结果也正序存放。
分析：
1）当两个链表长度不相同时，则应该用0头插法来填充较短的链表。
2）结果为正序存放，所以需要采用头插法建立和链表。
--------------------
（八）给定一个有环的链表，返回链表环的开头节点。
（1）检测链表是否有环？
1）方法：快慢两个指针fast和slow。
2）分析：fast一次走两步，slow一次走一步，会不会fast越过slow?
不会，反证法：
假设越过了，fast处于i+1位置，slow处于i位置，那么前一步fast处于i-1,slow也处于i-1，已经相遇了。
其他：
如果不考虑空间复杂度，可以使用一个map记录走过的节点，当遇到第一个在map中存在的节点时，就说明回到了出发点，即链表有环，同时也找到了环的入口。
不适用额外内存空间的技巧是使用快慢指针，即采用两个指针walker和runner，walker每次移动一步而runner每次移动两步。当walker和runner第一次相遇时，证明链表有环
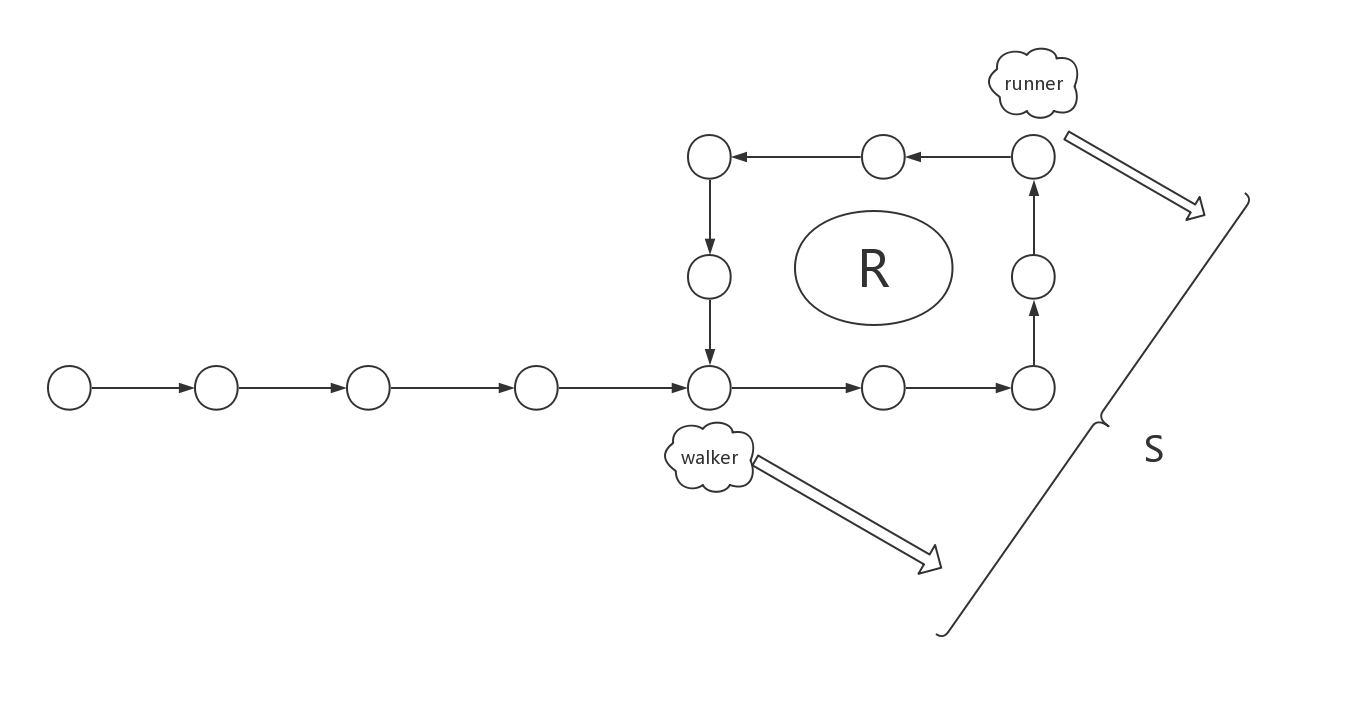
分析：
以图片为例，假设环的长度为R，当慢指针walker走到环入口时快指针runner的位置如图，且二者之间的距离为S。在慢指针进入环后的t时间内，快指针从距离环入口S处走了2t个节点，相当于从环入口走了S+2t个节点。而此时慢指针从环入口走了t个节点。
假设快慢指针一定可以相遇，那么有S+2t−t=nR，即S+t=nR，如果对于任意的S，R，n，总可以找到一个t满足上式，那么就可以说明快慢指针一定可以相遇，满足假设(显然可以找到);
由于S<R，所以在慢指针走过一圈之前就可以相遇; 即： S+t=R
所以如果链表中有环，那么当慢指针进入到环时，在未来的某一时刻，快慢指针一定可以相遇，通过这个也就可以判断链表是否有环;
（2）什么时候相遇？
假设这个链表有一部分不存在环，设长度为k、
当slow走了p步，fast走了2p步。所以当slow走了k步进入环时，fast走了2k步，离入口点为2k-k=k步，由于k可能大于环的大小loop_size,所以离环口应该是K=mod(k,loop_size),（用大K表示）。
综上：
1.slow处于环内的0步位置时；
2.fast处于环内的K步位置；
3.slow落后于fast，相离K步；
4.fast落后于slow，相离loop_size-K步；
5.每过一个单位时间，fast就会更加接近slow一步。
什么时候相遇？
如果fast落后于slow，相距loop_size-K步，每经过一个单位时间，fast就接近slow一步，那么两者将在loop_size-K步之后相遇。此时两者与环口处距离K步（因为下次走到环口需要K步,所以相遇点到环口距离为K,环口到相遇点的距离为loop_size-K），相遇位置定义为collisionSpot(相撞点)。
观点2：
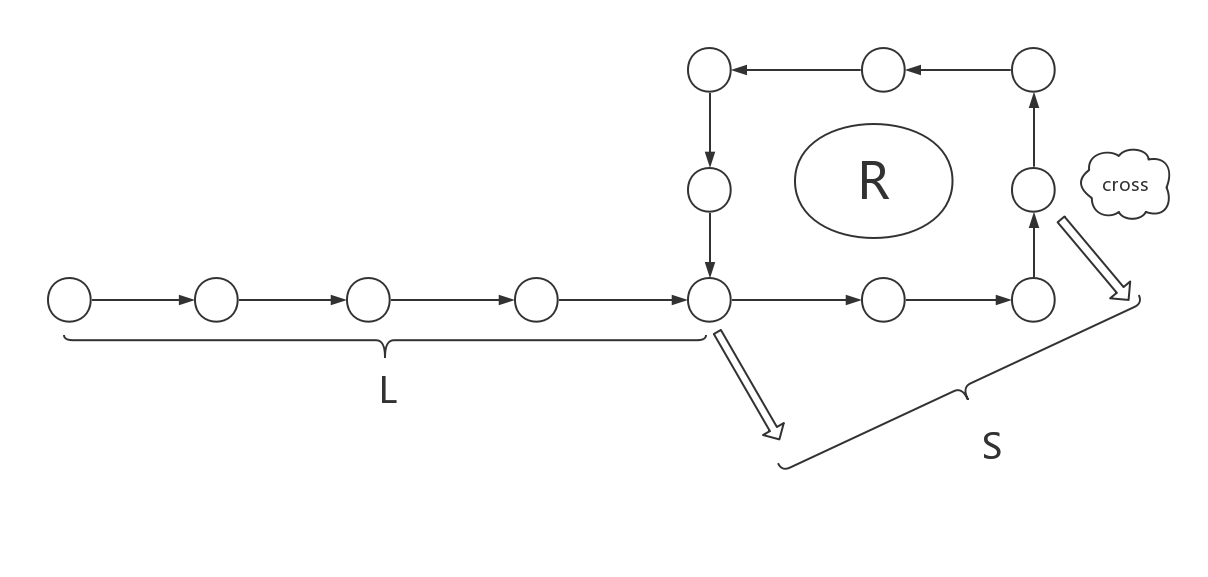
以图片为例，假设环入口距离链表头的长度为L，快慢指针相遇的位置为cross，且该位置距离环入口的长度为S。考虑快慢指针移动的距离，慢指针走了L+S，快指针走了L+S+nR(这是假设相遇之前快指针已经绕环n圈)。由于快指针的速度是慢指针的两倍，相同时间下快指针走过的路程就是慢指针的两倍，所以有2(L+S)=L+S+nR，化简得L+S=nR；
当n=1时，即快指针在相遇之前多走了一圈，即L+S=R，也就是L=R−S，观察图片，L表示从链表头到环入口的距离，而R−S表示从cross继续移动到环入口的距离，既然二者是相等的，那么如果采用两个指针，一个从表头出发，一个从cross出发，那么它们将同时到达环入口。即二者相等时便是环入口节点；
当n>1时，上式为L=nR−S，L仍然表示从链表头到达环入口的距离，而nR−S可以看成从cross出发移动nR步后再倒退S步，从cross移动nR步后回到cross位置，倒退S步后是环入口，所以也是同时到达环入口。即二者相等时便是环入口节点所以寻找环入口的方法就是采用两个指针，一个从表头出发，一个从相遇点出发，一次都只移动一步，当二者相等时便是环入口的位置；
（3）如何寻找环口点？
相遇处于环口相距K个节点。由于K=mod(k,loop_size),所以k=K+M*loop_size;（k为链表起始点到环口loopStart的距离，K为相遇点到环口的距离）所以可以定义两个指针，一个从链表头开始，一个从相遇collisionSpot开始，以同样的速度前行，则必定相遇。
(其实：相遇时collisionSpot距离链表的起点的距离为k+loop_size-K=K+M*loop_size+loop_size-K=
n*loop_size;)
（4）实现：
LinkNode* findLoopStart(LinkNode* list){
LinkNode* slow=list;
LinkNode* fast=list;
while(fast!=NULL && fast->next!=NULL){
slow=slow->next;
fast=fast->next->next;
if(slow==fast){
break;
}
}
if(fast==NULL || fast->next==NULL)//没有环
return NULL;
slow=list;//slow指向首部
while(slow!=fast){
slow=slow->next;
fast=fast->next;
}
return fast;
}
(5) 环的长度
方法一：
利用上面求出的环入口，再走一圈就可以求出长度；
即记录下环入口的指针，从入口处开始走，下次指针=入口的指针时，就算出了环的长度；
方法二：
当快慢指针相遇时，继续移动直到第二次相遇，此时快指针移动的距离正好比慢指针多一圈；
---------------------------
（九）单链表在O(1)删除指定的节点
（1）思路一：
要在单链表中删除一个节点i，最常规的做法就是从单链表的头结点开始，顺序遍历查找要删除的节点，并在链表中删除该节点；
之所以需要从开头开始查找，是需要得到被删除节点的前一个节点h;
（2）思路二：
可以将待删除结点的数据，和它的后续结点的数据进行互换，然后对它的后续结点进行删除操作，以此来达到 O(1) 时间复杂度的单链表删除。
因为后续节点的前驱节点就是自己，删除后续节点很容易；
ps: 这种思路还有一个问题，如果被删除的节点是尾节点，它没有下一个节点，我们必须从头结点开始遍历，得到倒数第二个节点，然后删除尾节点。
void RemoveListNode(List& l, ListNode* pDelNode)
{
if (l._head == NULL || pDelNode == NULL)
return;
if (pDelNode->_next != NULL) //要删除的节点不是尾节点
{
ListNode* pNext = pDelNode->_next;
pDelNode->_data = pNext->_data;
pDelNode->_next = pNext->_next;
delete pNext;
pNext = NULL;
}
else if (pDelNode == l._head) //链表只有一个节点
{
delete pDelNode;
pDelNode = NULL;
l._head = NULL;
}
else //链表有多个节点，删除的节点为尾节点
{
ListNode* cur = l._head;
while (cur->_next != pDelNode)
{
cur = cur->_next;
}
cur->_next = NULL;
delete pDelNode;
pDelNode = NULL;
}
}
分析：
对于n-1个非尾节点，我们可以在O（1）时删除节点，对于尾节点，由于要顺序查找，时间复杂度为O（n）。因此平均时间复杂度为[（n-1）*O（1）+O（n）]/n，结果还是O（1）。
受到O（1）时间的限制，该函数必须要求调用者保证被删除的节点确实在链表中，否则我们仍需要O（n）的时间才能判断链表中是否包含该节点。
扫一扫
935
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
