对称问题/回文问题



对称symmetry/回文palindrome问题：

（一）将字符串翻转

（二）判断是否对称/回文

（三）寻找一个字符串的最大对称子串

=============

（一）将字符串翻转

void reverse(char *str){
char *end =str;
char tmp;
if(str){
*end = *(str + (strlen(str)  - 1 ));
}

while(str<end){
tmp=*str;
*str++=*end;
*end--=tmp;
}
}

-------

（二）判断是否对称/回文

（1）回文定义：
回文即对称，如"abcba","abba";

（2）实现

方法一：从两端开始向中间扫描，知道相遇，对应的元素都一样，则是对称的，否则不是。

bool isSymmetry(const char * str,int left ,int right){
 while(left<right){
  if(str[left]!=str[right])
  return false;

  else {
  left++;
  right--;
  }
 }

 return true;
}

方法二：从中间向两边扫描；

/*长度为：len=right-left+1*/
bool isSymmetry(char * str ,int left, int right){
 
 int halflen=(right-left)/2;

 int mid1=halflen+left;//mid1往左边扫描
 int mid2=right-halflen;//mid2往右边扫描

  for(int i=0;i<=halflen;i++){
   if(str[mid1-i]!=str[mid2+i])
   return false;
  }
  return true;
}

//此中似乎没有考虑奇数以及偶数；

方法三：将字符串逆序（栈实现），然后扫描两个字符串，如果一直相等，则是回文。

---------
（三）寻找一个字符串的最大对称子串

（1）方法一：

1）分析：
 查找最大对称子串，应该从最大长度开始，找到则返回。不可以从最小的开始。

2）代码实现：

/*时间复杂度为O(n^3)*/
char * max_SubSymmetryStr(char * str, int length){

 char* subString=(char *) malloc(sizeof(char)*length);
  int Symmetry;//判断是否对称

 for(int len=length;len>0;len--){
   for(int j=0;j+len-1<length;j++){

//j,j+len-1分别是长为len的字符串的首字符和最后一个字符的下标。

   subString=str.subString(j,j+len-1);
    //获取str的从j到j+len的子串。

   Symmetry=isSymmetry(subString ,0,len-1);

   if(1==Symmetry)
    return subString;
   }

 }
 }

（2）方法二：中心扩展法；
1）思想：

时间复杂度O（n^2）,空间复杂度为O（1）。

中心扩展法的思路是，遍历到数组的某一个元素时，以这个元素为中心，向两边进行扩展，如果两边的元素相同则继续扩展，否则停止扩展。如下图：当遍历到3时

存在的问题：

 

1，2，2，1是一个回文串，然而找不到对称中心，这样以一个元素为中心向两边扩展就不好用了，这里有一种比较方便的处理方式，就是对1，2，2，1进行填充，比如说用#进行填充如下：

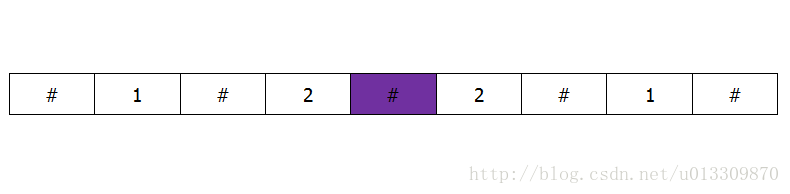
如下图这样填充之后就又成了一个中心对称的回文串，因此对于一个串进行处理时，先进行扩充，这样可以使中心扩展时比较方便，不用对非中心对称的子串进行特殊处理。假设填充前的子串长度为 len 那么扩充或的长度为：2 * len+1；

 

2）代码实现：

    char* longestPalindrome(char* s)
    {
        int len = strlen(s);
        if (len <= 1) { 
            return s; 
        }
        int start = 0;
        int maxlen = 0;

        //i表示中间元素下标
        for (int i = 1; i < len; i++)
        {

            /*

                    以i为中间节点的回文长度分别为奇数和偶数，来计算最大回文长度；

                    和保持的最大回文的长度进行对比；

                    start 记录最终的最大回文的起始地址；

                    maxlen记录最终的最长回文的长度；

           */

            //回文为偶数长度，i为中心点；abba，即b为中心点；则起始low和high的位置差1；
            int low = i - 1;
            int high = i;
            while (low >= 0 && high < len && s[low] == s[high])
            {
                low--;
                high++;
            }

            if (（high-1） - （low+1）+ 1 > maxlen)
            {
                //上面的循环结束条件为：s[low] ！= s[high]；那么前一个high节点和前一个low节点应该是相等的；
                // 所以长度为： （high-1） - （low+1）+ 1 即 high - low - 1；
                maxlen = high - low - 1;
                start = low + 1;
            }

            //回文为奇数长度，i为中心点；abcba，即c为中心点;则起始 low和high的位置差2；
            low = i - 1; 
            high = i + 1;
            while (low >= 0 && high < len && s[low] == s[high])
            {
                low--;
                high++;
            }
            if (high - low - 1 > maxlen)
            {
                maxlen = high - low - 1;
                start = low + 1;
            }
        }
        
        char *arr = (char *)malloc(sizeof(int) * (maxlen * 2));
        int i = 0;
        for (; i < maxlen; i++)
        {
            arr[i] = s[start++];
        }
        arr[i] = '\0';
        return arr;
    }