4.6 素数函数

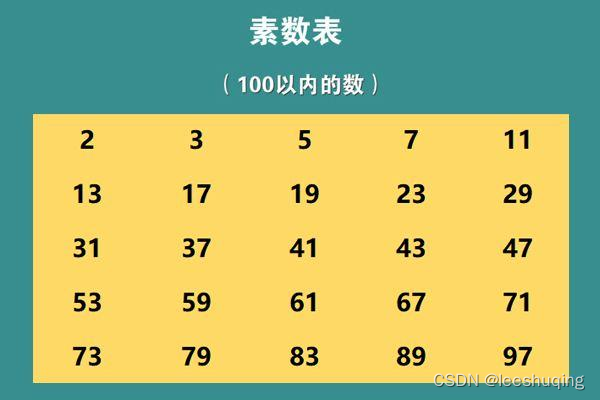
这里介绍一个素数函数的练习。

首先需要解决如何判断素数。素数也称质数，指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

那么具体的判断思路是什么？这是编程写代码的基础。比如对于7这个数，我们可以使用2到7之前的所有整数（即2到6），分别去除这个7，比如先使用2：

如果不能整除，就继续下一个3：

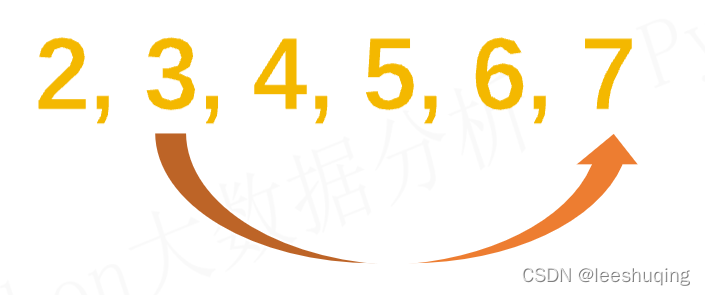
 还不能，就继续，直到6为止：

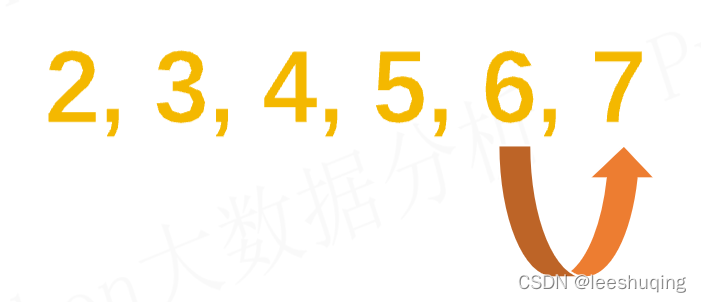
如果在全部的除法运算中，没有发生一次整除，就表明这个7就是素数。反之，有些数，可能就会发生被整数的情况，如8在除以2时发生整除，就表明8不是素数：

 按照这个思路，可以写出伪代码：

取出每一个数 i
    取出 2 到小于当前整数的每一个整数 j
        i 除以 j
        如果可以整除，说明 i 不是素数
    如果都没有整除，说明当前 i 是素数，并输出

这是第一份实现的代码：

for i in range(2, 101):
    isPrime = True
    for j in range(2, i):
        if i % j == 0:
            isPrime = False
    if isPrime:
        print(i)

输出为2到100之间所有素数。

这里定义了一个变量isPrime，它的主要目的是用于标记当前数是否为素数。为什么要定义？因为判断素数是在循环中来实现的，但是输出结果是在循环结束后才进行。因此，通过定义变量，就可以标记在循环中判断是否为素数，然后在循环后就可以根据这个变量得知刚才循环判断的结果。

对于每个需要判断素数的整数，isPrime初始值都是真，表示假设每个当前整数都是素数。一旦在从2到小于当前整数的除法运算中发生了整数，就表示当前整数不是素数，因此将isPrime再次设置为假。最后，到循环结束后，就根据这个isPrime是否为真，来决定是否输出。

这里最后的判断语句条件也可以写成下面的写法，意思一样：

for i in range(2, 101):
    isPrime = True
    for j in range(2, i):
        if i % j == 0:
            isPrime = False
    if isPrime == True:
        print(i)

也可以使用变量表示不是素数，效果一样：

for i in range(2, 101):
    isNotPrime = False
    for j in range(2, i):
        if i % j == 0:
            isNotPrime = True
    if not isNotPrime:
        print(i)

接下来，就可以进一步考虑执行效率的问题。还是看下一开始那个例子：

此时，对于8而言，一旦有一个数可以整除，说明8不是素数，其实也就没有必要再以3判断是否整除。

for i in range(2, 101):
    isPrime = True
    for j in range(2, i):
        if i % j == 0:
            isPrime = False
            break
    if isPrime:
        print(i)

这个代码的关键在于循环中的判断语句增加了break语句，一旦整除发生，即结束当前数和其他后续整数的整除判断。

---

接来下，我们增加下整除比较次数统计，看看这种写法究竟提高了多少效率？

这是增加了次数统计的原始版本：

count = 0
for i in range(2, 101):
    isPrime = True
    for j in range(2, i):
        count += 1
        if i % j == 0:
            isPrime = False
    if isPrime:
        print(i)
print(count)

输出的最后一行为：4851

这是增加了次数统计的改进版本：

count = 0
for i in range(2, 101):
    isPrime = True
    for j in range(2, i):
        count += 1
        if i % j == 0:
            isPrime = False
            break
    if isPrime:
        print(i)
print(count)

输出的最后一行为：1133。看得出，减少了3/4的不必要比较。

能不能再提高效率？比如是不是所有的数都要去判断是否为素数？偶数显然就没有必要去判断是否为素数。这里为了避免复杂，只考虑3及以后的整数。

for i in range(3, 101, 2):
    isPrime = True
    for j in range(2, i):
        if i % j == 0:
            isPrime = False
            break
    if isPrime:
        print(i)

代码的改进在于改变了循环取整数的方式，从3开始，每次步幅为2，依次取到100，这些正好是第一个循环中range函数参数的设定内容。

此时统计比较次数：

count = 0
for i in range(3, 101, 2):
    isPrime = True
    for j in range(2, i):
        count += 1
        if i % j == 0:
            isPrime = False
            break
    if isPrime:
        print(i)
print(count)

输出的最后一行为：1084

能不能再提高代码执行效率？是不是所有的数都要去除？ 比如7：

如果2已经除过，其实就没有必要再去除以3、4、5和6，原因很简单。7的开方是2.65，和比开方小的整数进行除法操作得到的商一定是大于比开方大的数，因此，如果和比开方小的整数进行除法操作都没有整除，也必然意味着比开方大的整数进行除法操作也不会整除。

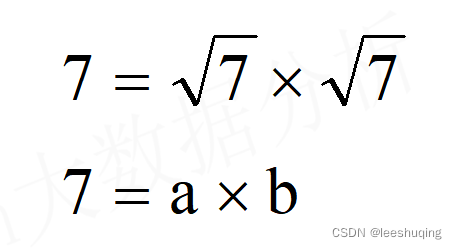
因此，可以在进行整除循环时，无需比较从2到小于当前数的所有整数，而只要比较从2到小于当前数开方的最大整数即可：

import math

for i in range(3, 101, 2):
    isPrime = True
    for j in range(2, int(math.sqrt(i)) + 1):
        if i % j == 0:
            isPrime = False
            break
    if isPrime:
        print(i)

此时统计比较次数：

import math

count = 0
for i in range(3, 101, 2):
    isPrime = True
    for j in range(2, int(math.sqrt(i)) + 1):
        count += 1
        if i % j == 0:
            isPrime = False
            break
    if isPrime:
        print(i)
print(count)

输出的最后一行为：187。这一次效率提升最为明显。

---

我们再次回到代码编写逻辑上来。标记变量isPrime是这个代码中非常重要的变量，但是可以不可以使用标记变量？也就是说，利用整除比较过程中的一些特征，即可观察出是否为素数，而不是非要通过设置一个标记变量，这可能吗？

我们以这个代码开始：

import math

for i in range(3, 101, 2):
    for j in range(2, int(math.sqrt(i)) + 1):
        if i % j == 0:
            break
    if isPrime:
        print(i)

可以看出，如果是素数，整除在整除循环还没结束时就已经发生，并且会提前终止当前的整除循环，这会导致 j 变量的取值无法达到所在循环的下限！反之，如果是素数，j 变量值一定可以达到循环的下限。因此，不妨就利用这个特征：

for i in range(3, 101, 2):
    for j in range(2, i):
        if i % j == 0:
            break
    if j == i - 1:
        print(i)

输出效果一致。但是这里取消了标记变量，就是利用 j 的取值是否达到所在整除循环的下限，如果达到了，则没有发生过整除，则就是素数！

同时，巧妙的利用Python语言的特点也可以实现一种：

for i in range(3, 101, 2):
    for j in range(2, i):
        if i % j == 0:
            break
    else:
        print(i)

输出效果一致。循环的else语句只要在循环全部遍历完后才会被执行，一旦有break提前结束，则不会执行。这个效果正好等价于如果是素数（循环全部遍历完）才会被执行（即输出），一旦不是素数（有整除，导致break提前结束）就不执行。

---

最后，到了封装函数的时候了。我们希望这个函数能够这样使用：

print(isPrime(7))

输出为：True。

整体思路如：

 最终得到函数：

def isPrime(num):
    for j in range(2, num):
        if num % j == 0:
            break
    else:
        return True
    return False

可以看出，函数的定义，关键在于代码逻辑的实现，实现好后，只需将被处理的数据换成形参，加上函数头，输出换成返回值，即可完成函数的定义。

配套学习资源、慕课视频：

Python大数据分析-李树青 (njcie.com)http://www.njcie.com/python/