2.1 变量的使用

变量的使用好比给你起名字。在数据分析中，我们需要处理很多数据，但是这些数据本身并不好记忆，而且还有很多相同的数据，比如两个相同的身高数据。所以为了方便，我们可以给这些不同的数据起个不同的名字。

在Python语言中，变量定义方法很简单，就是变量名加上赋给的初始值。

num = 1

这个意思是说定义了一个变量，名称是num，它的初始值为1。可以想象，我们把1这个整数装进一个叫做num的抽屉。相对于变量，这个1我们称之为常量。因此，变量初始值一般都可以通过常量来设置。

还有很多初学者觉得很变扭，觉得为什么变量赋值使用等于号？这些其实都是习惯，有些计算机语言采取了诸如“：=”等方式。这也是为什么大家需要多练习，多练习后就会习惯。

之所以叫常量，是因为1不可被改变，如果变了，那就成为另一个常量了，不像变量，可以根据需要存储不同的数值。

num = 1
print(num)
num = 2
print(num)

运行界面为：

程序的第二个输出为2，表示num变量数值已经在第二次赋值为2时被改变了，原有的1已经丢失，变量数值发生了变化。

再如我们定义两个身高：

height1 = 1.80
height2 = 1.76

和刚才差不多，只是这次我们将一个小数装进了变量。小数有时也称为浮点数，原因是英文小数float也有浮动的意思。

在这里，虽然有各种各样的数据，但是在Python中常见的数据种类并不多，除了整数和小数外，常见的还有一个就是字符类型，也称为字符串。我们前面也给大家说明过：

name = '大学生'

请注意，字符串常量需要前后加上单引号或者双引号，否则和变量名称（变量名称可以看成是没有前后单引号的字符串，在Python只表示变量名称和函数名称等特殊用途）就不好区分，从而产生问题。

另外还有布尔型，即真假表示的变量。

isStudent = True

注意，这里的True必须严格大小写书写，表示真，使用False表示假。这些特殊的名称代表着真假这两个常量。

很多同学都喜欢使用中文输入，但是所有的计算机语言几乎都规定除了变量名称和字符串常量外，所有符号都需要使用英文半角字符，请大家一定要注意及时切换输入法。比如这里的等于号其实是中文全角，运行提示非法字符：

同时注意大小写的区别！

num = 0
print(NUM)

运行界面为：

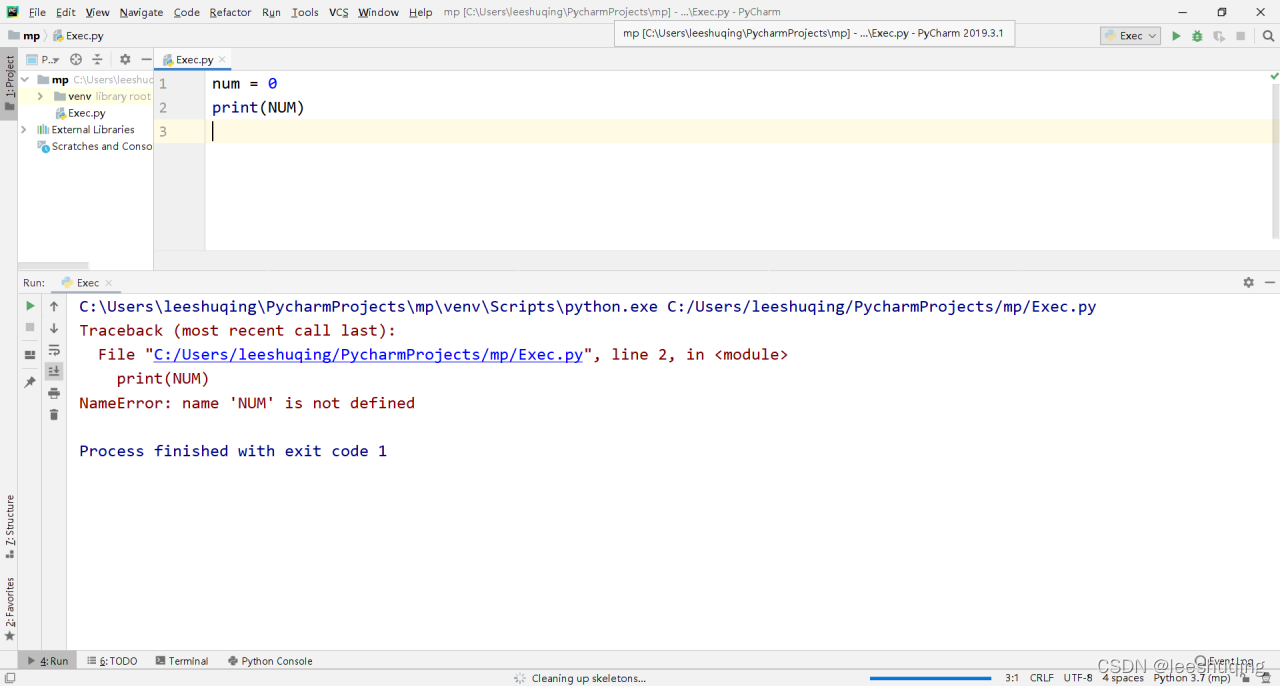
错误提示说NUM没有定义（not defined），因为大写和小写被看成不同的变量名称。 

还有一种常见的初学者错误，就是先使用（读取）变量，然后才定义（或者根本没有对该变量赋值过）

print(num)
num = 0

运行界面为：

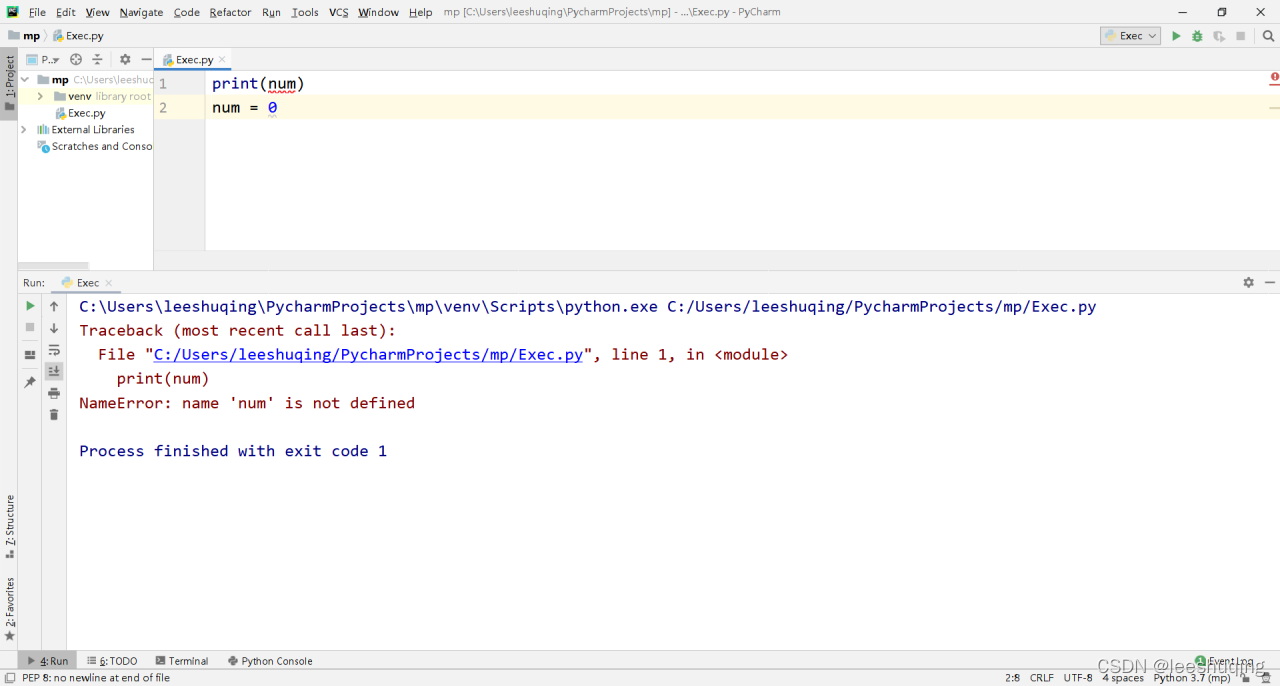
此时运行的错误还是表示num没有定义。这也有道理，如果可以，请问第一行的num数值是什么呢？毕竟还没有赋值过。因此，只有先创建变量才能使用变量，还没创建，当然不能使用。一般的创建，其实就是赋值，即先赋值后，才能使用。好比先存钱才能取钱一样。

变量名称并不可以随意起，一般建议使用字母、数字和下划线，同时不要以数字开头即可。另外，有些特殊的名称在Python有专门的用途，我们称之为关键字或者保留词（后面我们会不断接触到），大家也不要使用它们作为变量名称，如：

比如这个有代码就有问题，for不能成为变量的名称：

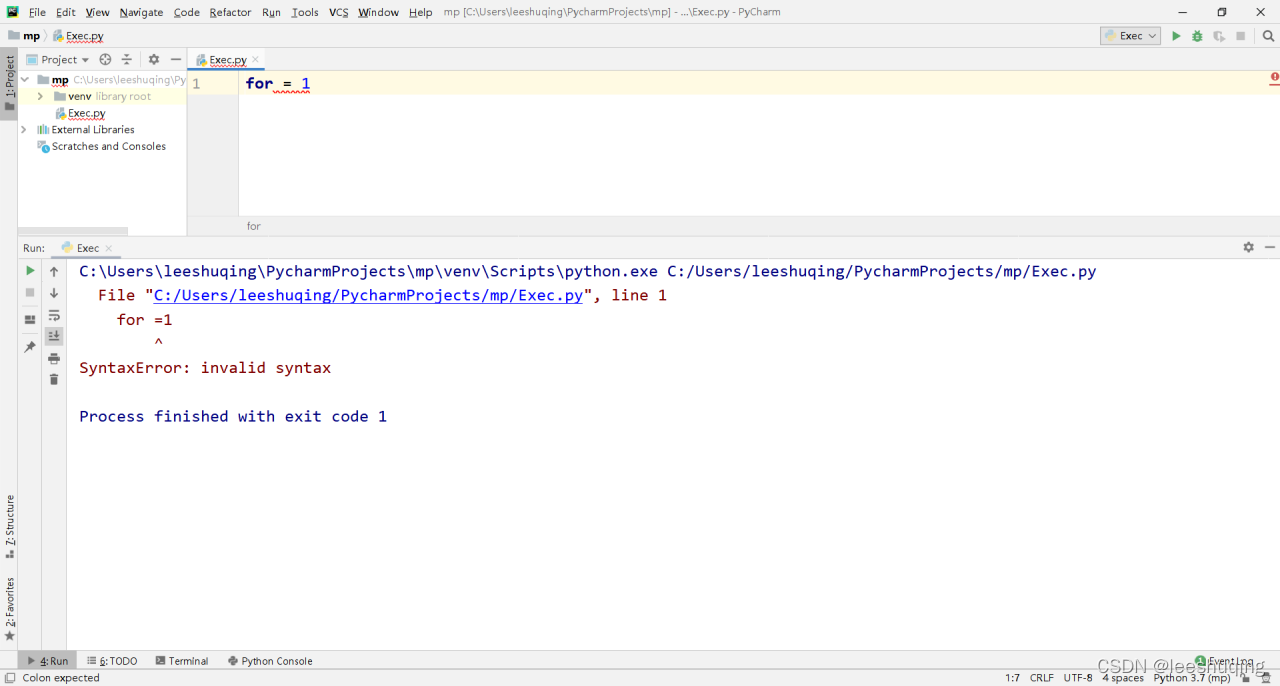
前文已经说明什么时候定义变量，如果你需要反复使用一个数据，或者需要在不同的地方使用同一个数据的话，那么就应该定义变量，并保存这个数据。

我们来做个练习，让用户输入两个数，加起来再输出：

num1 = input()
num2 = input()
print(num1 + num2)

这里之所以定义两个变量，就是为了存储两次不同的输入。运行界面中，先后输入了1和2两个数字：

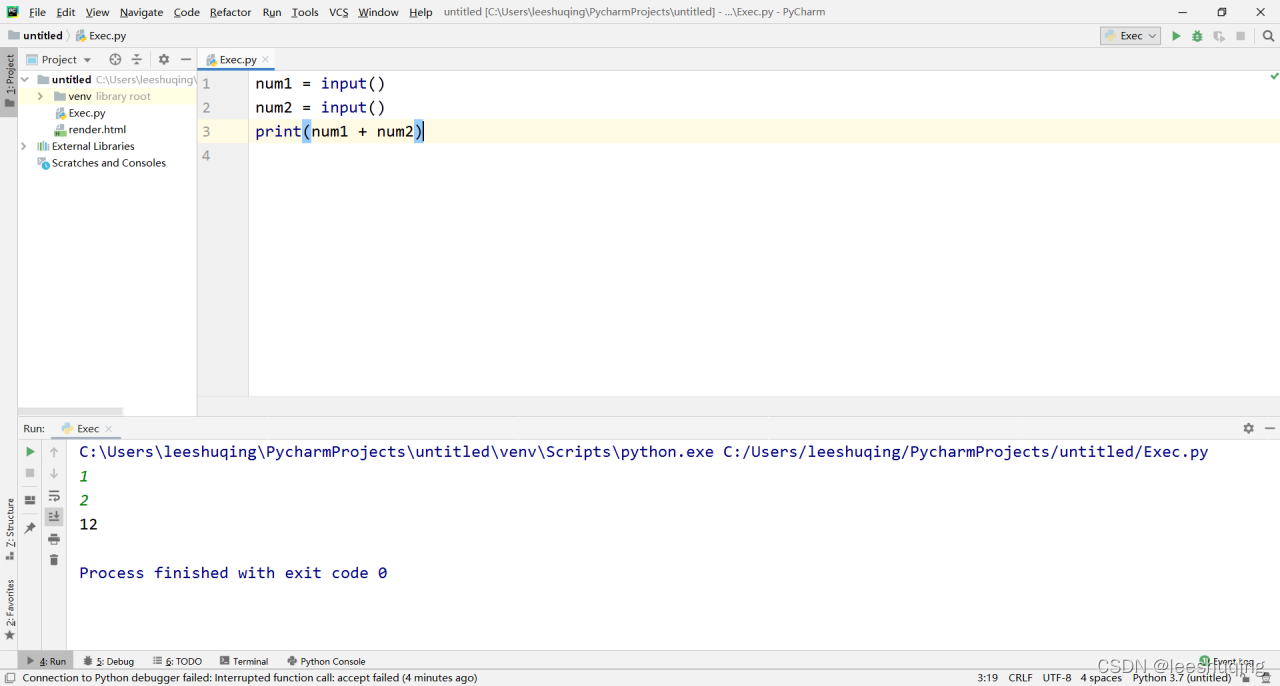
但是大家有没有觉得有问题？其实，这并非错误。默认情况下，input只能输入字符串，对于字符串来说，加号就是连接的意思，当然1+2=12。 

为了能够进行真正意义上的整数计算，我们必须要转换数据类型：

num1 = input()
num2 = input()
print(int(num1) + int(num2))

这里我们使用了int函数，它表示将字符串转换为整数。这里我们注意到我们把num1和num2分别放在int函数后面的圆括号内。

函数代表着一种功能，一般如果圆括号里没有内容，它的功能往往很固定。但是如果将数据传递到里面，作为函数的参数，函数将会根据传递参数数据的不同而展示不同的结果。比如此时就可以将传递进来的字符串转换为对应的整数。圆括号中的数据既可以是变量，也可以是常量。

很多函数都有参数，比如：

num1 = input('请输入整数1：')
num2 = input('请输入整数2：')
print(int(num1) + int(num2))

此时的input有了字符串参数，可以在输入前自动显示这个提示信息，效果更好。运行界面为：

其实，此时的print函数也有参数，就是两个整数的和，所以每次参数内容不一样，输出结果都不同。

我们来换种写法：

num1 = int(input('请输入整数1：'))
num2 = int(input('请输入整数2：'))
print(num1 + num2)

这样效果其实一样，但是也存在着差别。大家注意到，此时int函数是将input函数输入得到的字符串作为自己的参数，返回的就是对应的整数，因此，num1和num2一直都是存放着整数。

而在刚才的代码中，num1和num2一直都是字符串，直到输出时才临时转换为整数。因此，两者的差异主要体现在变量的数据类型不一样。大家必须要时刻留心变量的数据类型。同时，对于这样的问题，既然我们希望num1和num2表达整数，最好还是应该在接受完输入后立刻转换为整数，这样能避免后面很多不必要的临时数据转换。

当然，采取分离的写法也可以：

num1 = input('请输入整数1：')
num1 = int(num1)
num2 = input('请输入整数2：')
num2 = int(num2)
print(num1 + num2)

此时，第一行的num1存储的是字符串，但是第二行就变成了整数。这个没有问题，Python变量非常灵活，存储什么，变量就是什么类型。

当然，变量的定义也可以根据需要灵活选择：

num1 = int(input('请输入整数1：'))
num1 = num1 + int(input('请输入整数2：'))
print(num1)

这段代码只定义了一个变量，实现了和刚才一样的功能。这里的关键在于第二行。首先，对于采取等于号的赋值方法大家一定不能按照传统数学的相等判断来理解，它只是一个赋值标记，第二行的意思是将num1取出来，此时应该是刚才第一次输入后又转换整数的结果，然后再让用户输入一个字符串并转换为整数，两者相加，再重新放回num1中，显然，num1仍然保存了最终的整数相加结果。

但是由于我们只使用了一个变量，因此第一次输入的整数在累加后就丢失了，所以这也再次体现了变量定义的价值，如果后续你还要继续使用两次不同输入的数据，那么就应该单独建立变量保存。

对于多个变量，我们还可以使用一些更为简单的赋值方式：

num1, num2 = 1, 2
print(num1, num2)

它相当于：

num1 = 1
num2 = 2
print(num1, num2)

其中对于num1和num2的赋值，就是分别将两个常量分别赋给两个变量，print函数的输出使用逗号也表示输出两个变量，默认空格分隔。

利用这种写法有时也可以实现一些有趣的功能：

num1, num2 = 1, 2
num1, num2 = num2, num1
print(num1, num2)

运行界面为：

输出为2 1，利用这种方法可以实现不同变量数值之间的互换。

当然对于变量数值互换，我们还可以采用利用其他变量中转的方法来实现：

num1, num2 = 1, 2
num3 = num1
num1 = num2
num2 = num3
print(num1, num2)

输出也是2 1。大家可以自己思考下具体的数值互换过程。这里有一个示意图，大家可以自行思考下：

配套学习资源、慕课视频：

https://www.njcie.com/python/https://www.njcie.com/python/