线性模型笔记-Datawhale X 李宏毅苹果书 AI夏令营

模型在训练数据上表现很好，误差较小。但在没有见过的新数据上（即测试数据上），模型未必能够很好地预测，因此误差值会较大。

根据真实的数据情况调整写出新的模型，考虑了比较多的信息，加入了更多的权重，在训练数据上应该要得到更好的、更低的损失。

把输入的特征 x 乘上一个权重，再加上一个偏置就得到预测的结果，这样的模型称为线性模型。

线性模型也许过于简单，x1 跟 y 可能中间有比较复杂的关系。线性模型有很大的限制，这一种来自于模型的限制称为模型的偏差，无法模拟真实的情况。所以需要写一个更复杂的、更有灵活性的、有未知参数的函数。

分线段曲线可以看作是一个常数加一群Hard Sigmoid函数。Hard Sigmoid 函数的特性是当输入的值，当 x 轴的值小于某一个阈值（某个定值）的时候，大于另外一个定值阈值的时候，中间有一个斜坡。所以它是先水平的，再斜坡，再水平的。

直接写HardSigmoid 不是很容易，用 Sigmoid 函数来逼近 Hard Sigmoid,Sigmoid 函数的表达式为

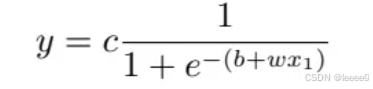
调整这里的 b、w 和 c 可以制造各种不同形状的 Sigmoid 函数，用各种不同形状的 Sigmoid函数去逼近 Hard Sigmoid 函数。

优化是找一个可以让损失最小的参数,参数少的时候可以穷举，参数多的时候用梯度下降。

所有的未知的参数，一律统称 θ，所以损失函数就变成 L(θ)。损失函数能够判断 θ 的好坏。

先给定 θ 的值，即某一组 W, b, cT, b 的值，再把一种特征 x 代进去，得到估测出来的 y，再计算一下跟真实的标签之间的误差 e。把所有的误差通通加起来，就得到损失。

然后进行优化，要找到 θ 让损失越小越好

使用梯度下降更新参数的过程：

关于模型的变形，还可以把HardSigmoid 可以看作是两个修正线性单元的加总，ReLU 的图像有一个水平的线，走到某个地方有一个转折的点，变成一个斜坡，其对应的公式为

   

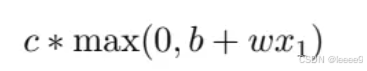
在机器学习里面，Sigmoid 或 ReLU 称为激活函数。

Sigmoid 或 ReLU 称为神经元（neuron），很多的神经元称为神经网络。每一排称为一层，称为隐藏层，很多的隐藏层就“深”，这套技术称为深度学习。

在训练数据和测试数据上的结果是不一致的，这种情况称为过拟合。