编译原理实验五-逆波兰表达式的产生及计算

• 实验目的

将简单算术表达式转换为用逆波兰式，并计算用逆波兰式的值，加深对逆波兰式在代码编译中的用途。本实验只需要支持正数即可。

• 实验内容

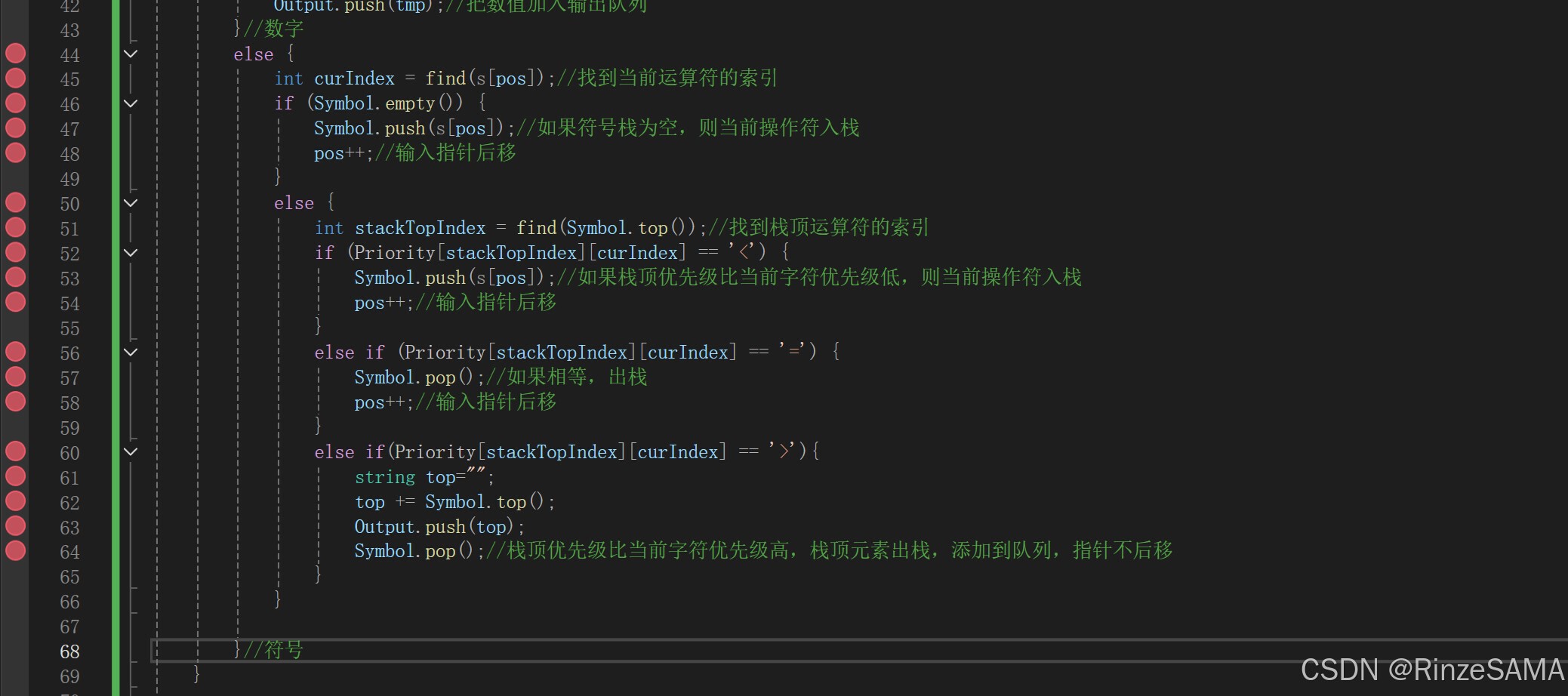
任务1：简单表达式转换成逆波兰式的原则如下：设置一个输出队列，设置一个符号栈，为了处理方便，可以在输入简单表达式的最后加一个#，然后遍历表达式中的每个单元

1读取新单元。

2是数值，则放入输出队列中，回到第1步，不是则下一步。

3是操作符(+-*/())，如符号栈顶为空或栈顶操作符优先级比当前操作符优先级低，则直接将当前操作符压入符号栈，回到第1步；如果栈顶操作符和当前操作符优先级相等，则直接回到第1步（这种情况只发生在栈顶的左括号遇到当前的右括号的时候）；其他情况将栈顶元素出栈，添加到队列，直到栈顶为空或者栈顶元素的优先级比当前操作符低，然后将当前操作符压入符号栈，回到第1步。

遍历结束后，将符号栈中剩余的符号都逐个弹出到输出队列中。此时输出队列中就是所要的逆波兰式。逆波兰式是不需要保存括号的。优先级关系参看课本P157的表5.2。

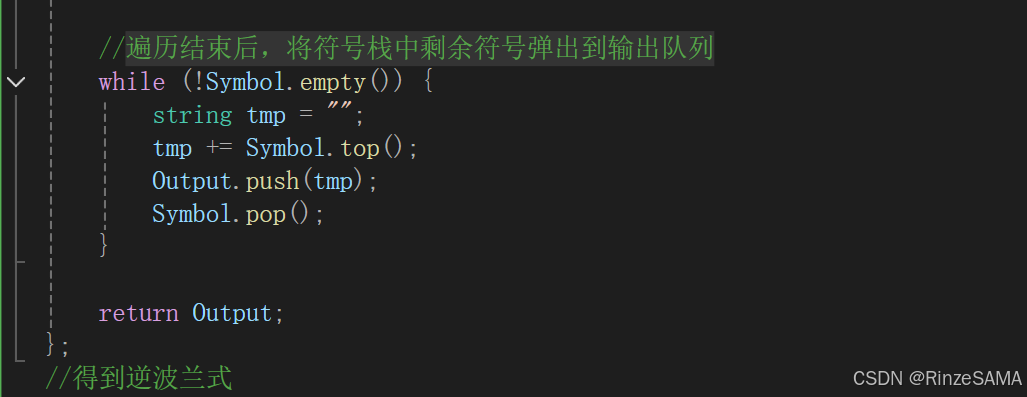
任务2：逆波兰式计算的原则如下：设置一个输出栈，从左到右遍历逆波兰式

1. 如果是数字，则压入输出栈
2. 如果是(+-*/)，则从输出栈弹出两个操作数，和操作符计算后，将结果压入输出栈

遍历完成后输出栈中的数值就是计算的数值。

计算值用double类型存储和输出。

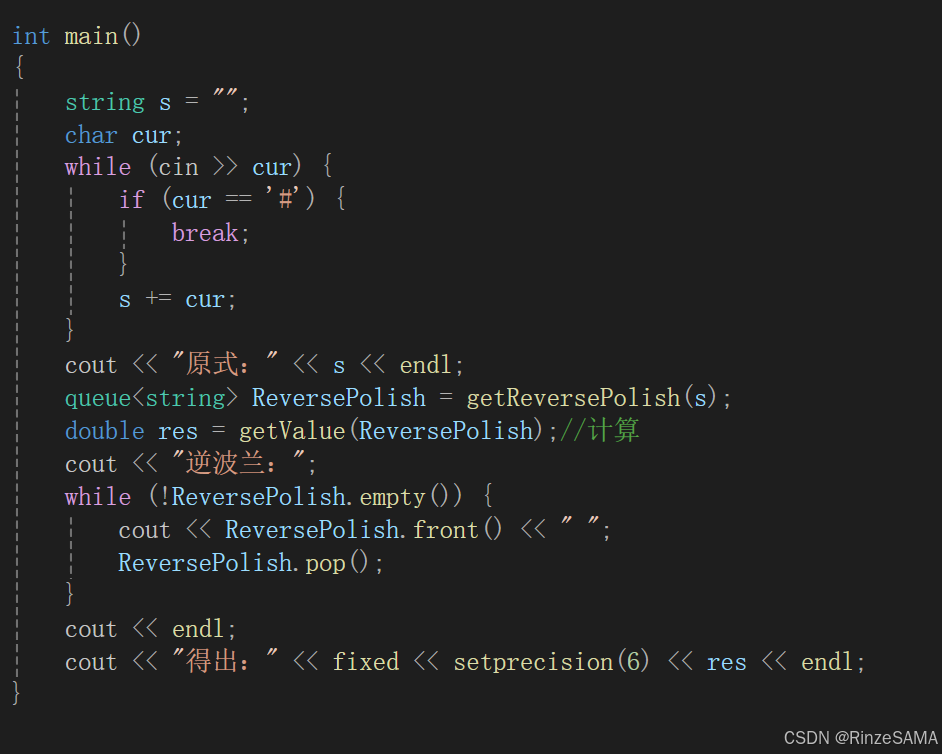
测试案例：

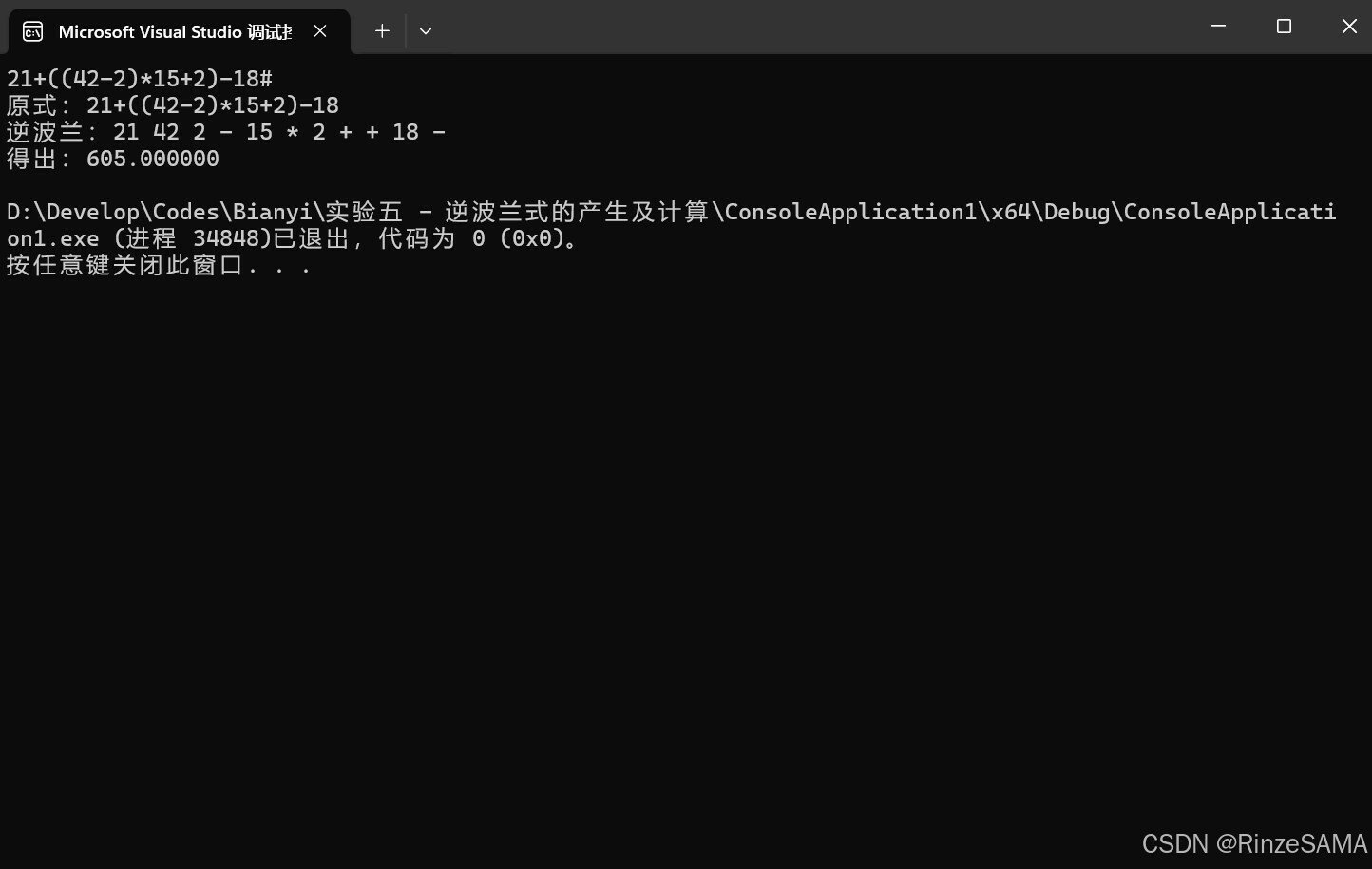
输入表达式21+((42-2)*15+2)-18#进行计算，结果如下：

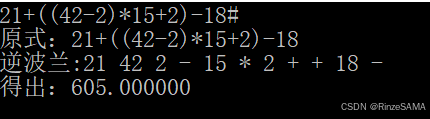
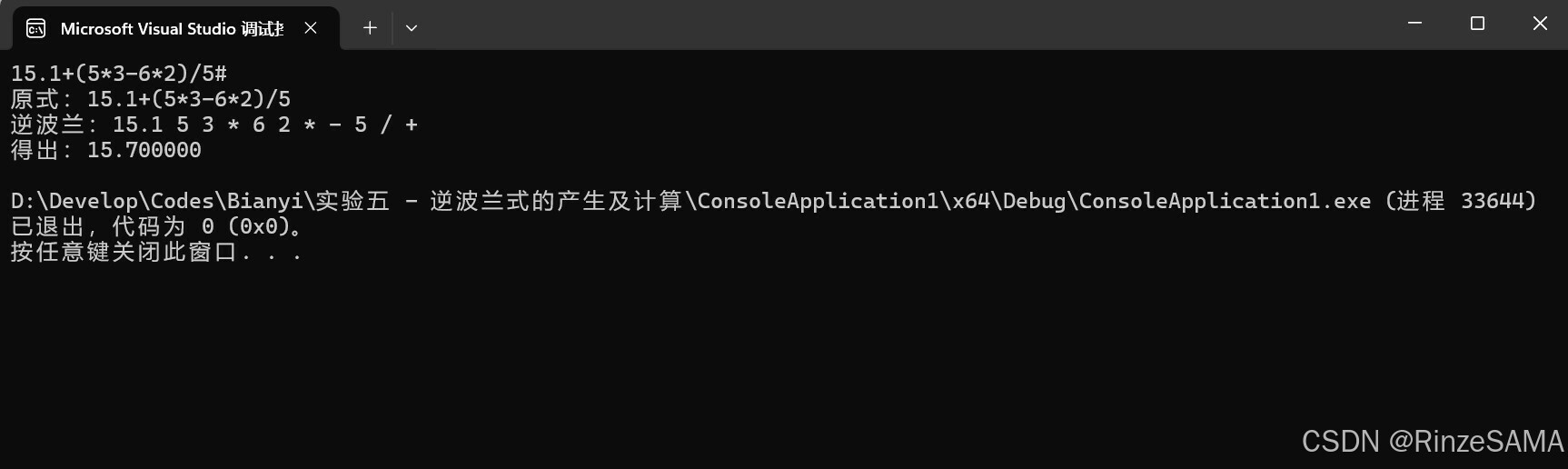
输入表达式15.1+(5*3-6*2)/5#进行计算，结果如下：

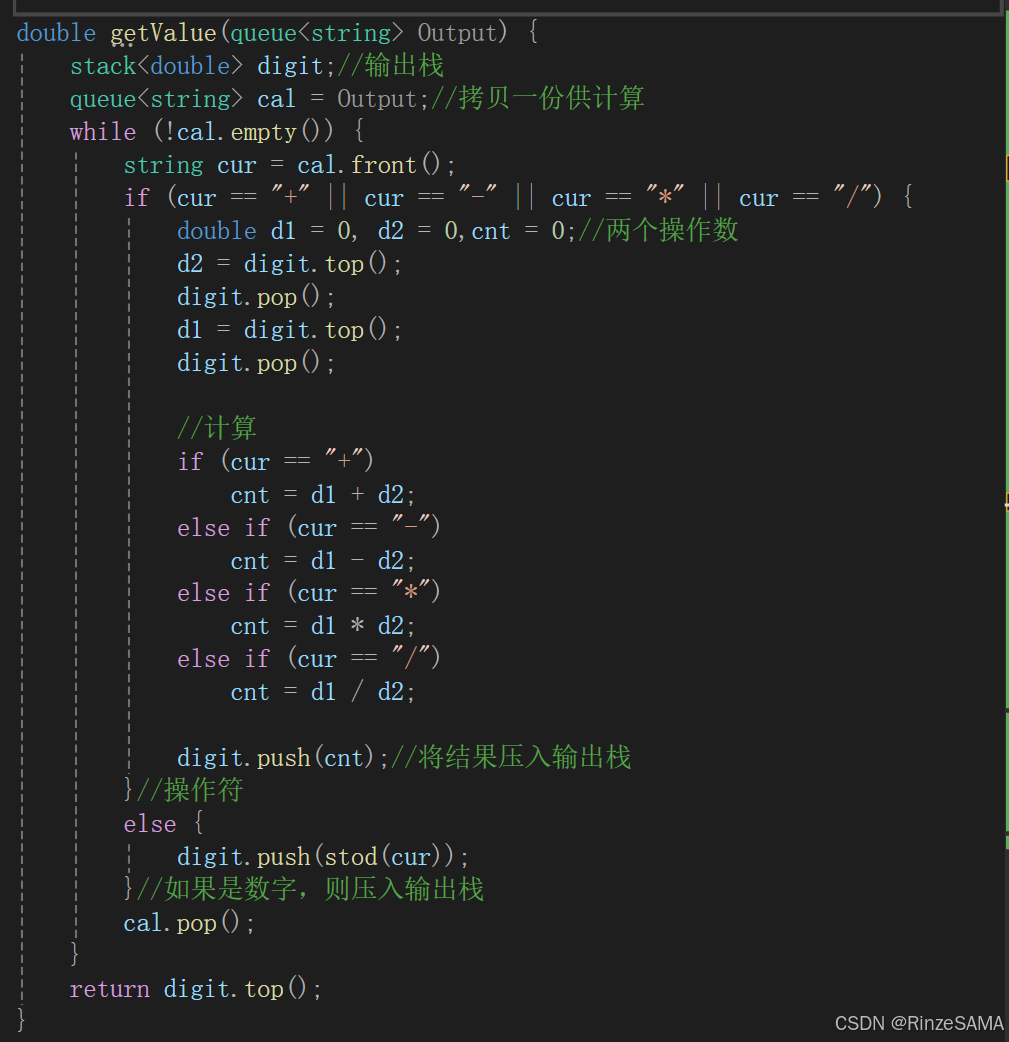
实验具体步骤

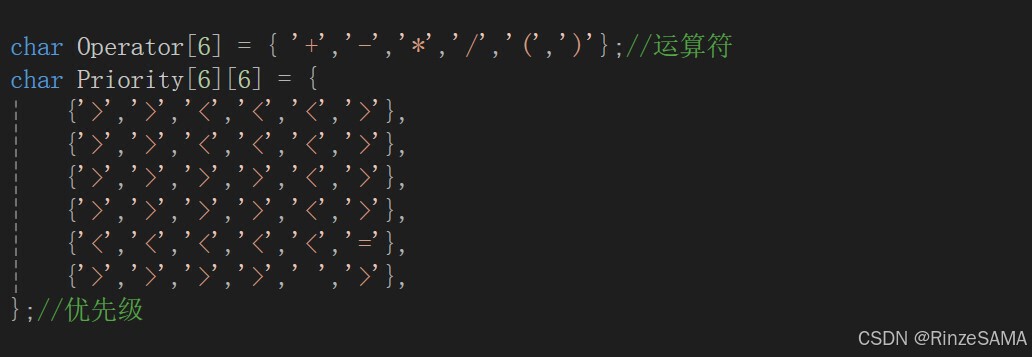
定义优先级，运算符。

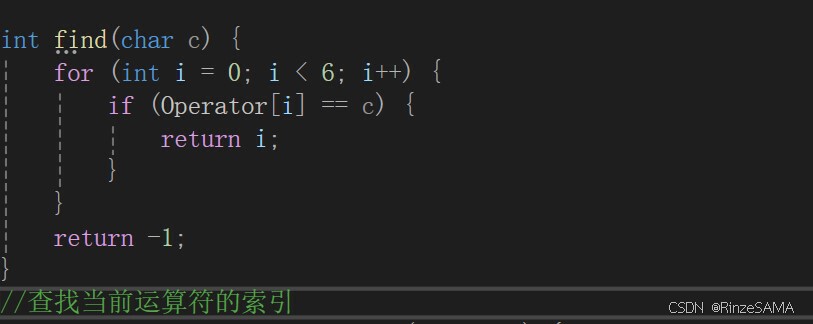
查找当前运算符的索引。

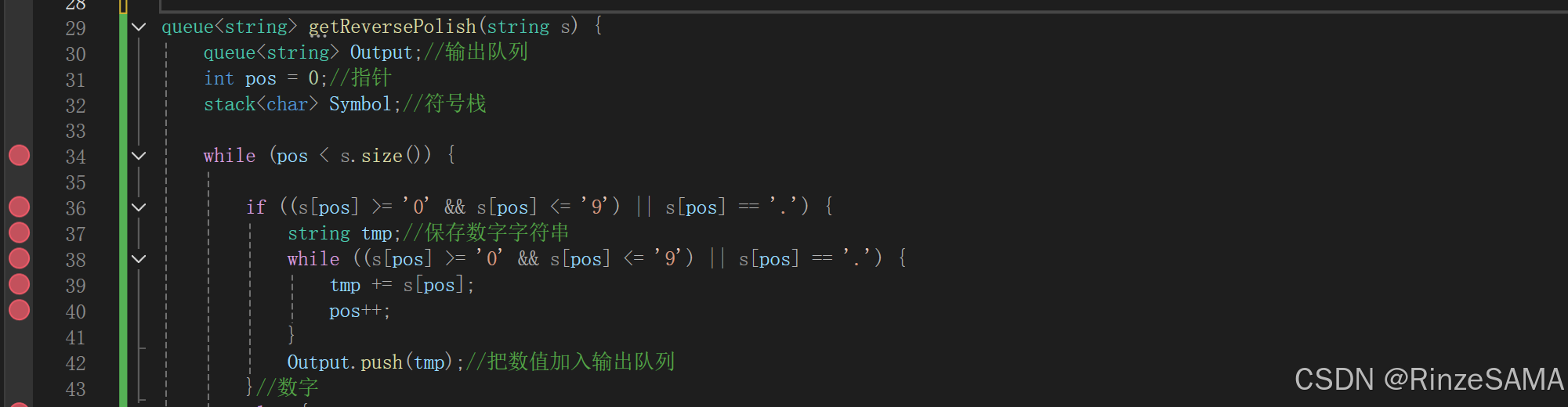
计算逆波兰表达式。当前为数字，考虑小数

计算逆波兰表达式。当前为运算符

遍历结束后，将符号栈中剩余符号弹出到输出队列

计算逆波兰表达式的值。

主函数

测试结果1：

测试结果2：