《挑战程序设计竞赛》1.6.1-先从简单题开始

最新推荐文章于 2022-03-27 18:42:20 发布

原创最新推荐文章于 2022-03-27 18:42:20 发布 · 281 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

算法专栏收录该内容

21 篇文章

订阅专栏

本文介绍了一个经典的计算机编程问题——如何从给定长度的棍子中选出三根能够组成三角形，并给出最大周长的算法实现。通过三重循环枚举所有组合并检查是否满足构成三角形的条件来解决此问题。

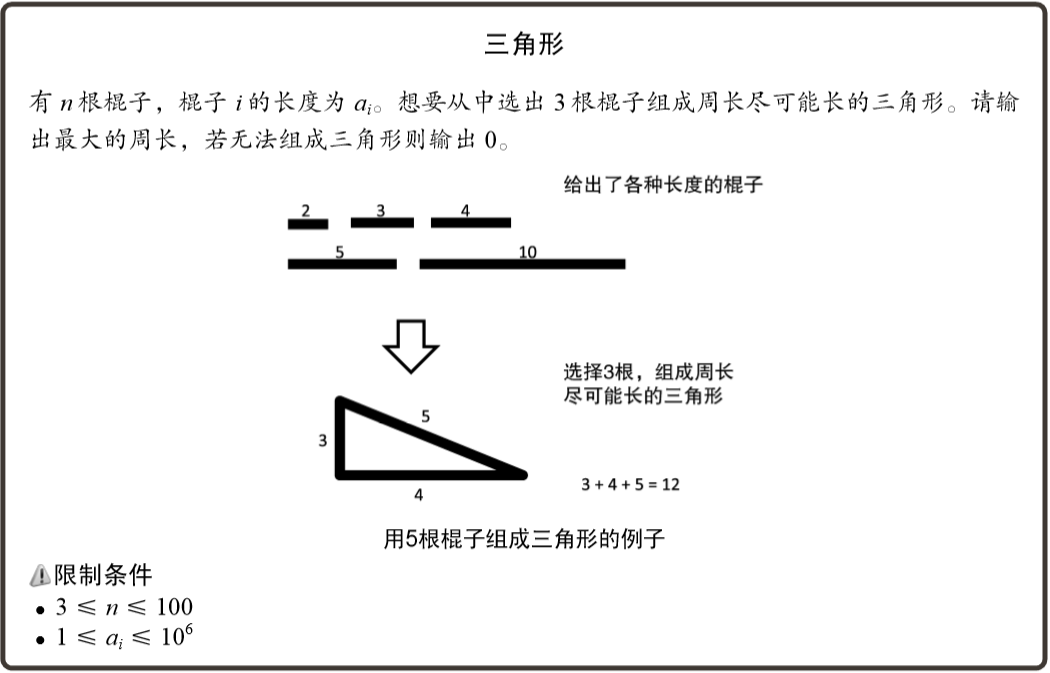
输入：

n = 5 n = 4

a = {2, 3, 4, 5, 10} a = {4, 5, 10, 20}

输出：

12（选择3、4、5时） 0（无论怎么选都无法组成三角形）

选择3根棍子，它们能组成三角形的充要条件为：长棍子的长度 < 其余两根棍子的长度之和。
于是我们可以试想这样一种算法：首先用三重循环枚举所有的棍子选择方案，再利用上式判断能否组成三角形。如果可以，那么该三角形的周长就是备选答案。

#include <stdio.h>
#define MAX_N 100
#define max(a,b)    (((a) > (b)) ? (a) : (b))
int main(void)
{
	int n, a[MAX_N];
	int ans = 0;          // 答案 
	
	scanf("%d", &n);
	for (int l = 0; l < n; l++)
		scanf("%d", &a[l]);
	
	// 让i < j < k,这样棍子就不会被重复选中了
	for (int i = 0; i < n; i++) {
		for (int j = i + 1; j < n; j++) {
			for (int k = j + 1; k < n; k++) {
				int len = a[i] + a[j] + a[k];           // 周长
				int ma  = max(a[i], max(a[j], a[k]));   // 最长棍子的长度 
				int rest= len - ma;                     // 其余两根棍子的长度之和
				
				if (ma < rest)
					// 可以组成三角形，如果可以更新答案则更新
					ans = max(ans, len); 
			}
		}
	} 
	
	// 输出
	printf("%d\n", ans);
	 
	return 0;
}