数据结构——排序算法总结

最新推荐文章于 2025-09-28 17:40:26 发布

原创

最新推荐文章于 2025-09-28 17:40:26 发布 · 1k 阅读

5 ·

CC 4.0 BY-SA版权

本文详细总结了各种排序算法，包括内部排序的插入排序（直接插入排序、折半插入排序、希尔排序）、交换排序（冒泡排序、快速排序）、选择排序（简单选择排序、堆排序）和归并排序、基数排序；以及外部排序的多路归并排序。分析了每种算法的算法思想、代码实现、性能特点（时间复杂度、稳定性、适用场合）。

知识框架

各种排序算法的时间复杂度总结对比：

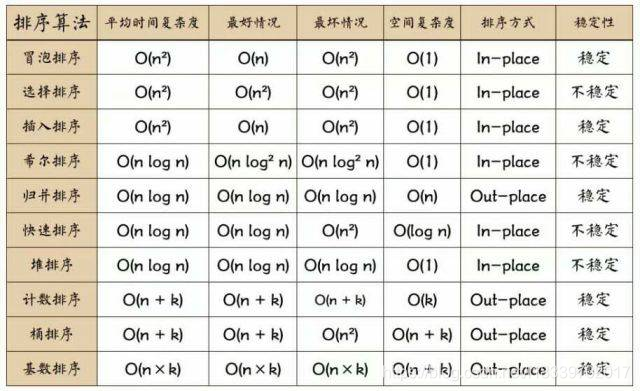
下文中，对于每种排序算法，将对其进行算法思想，代码实现，性能分析（时空复杂度，稳定性，使用场合）几个方面的分析。

1.内部排序

1.1 插入排序

插入排序是一种简单直观的排序方法，其基本思想是每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中，直到全部记录插入完成。

1.1.1 直接插入排序

1.1.1.1算法思想

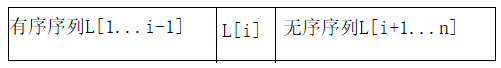
设待排序的记录存放在数组r[1...n]中，r[1]是一个有序序列。循环 n-1 次，每次将无序序列首个元素，按序插入到有序序列。

（个人的简单叙述：从第二个元素（i=2）开始准备插入。①判断当前元素是否需要插入到前面，if(a[i] < a[i-1]) 需要把a[i]插入到前面。②从i-1往前遍历查找应该插入的位置，同时把元素向后移空出插入的位置）

1.1.1.2代码实现：

//顺序表的实现
void InsertSort(int arr[], int len){
    for(int i = 2; i <= len; i++){//依次将arr[2]~arr[n]插入到前面已排序的序列
        if(arr[i].key < arr[i-1].key){
            //若arr[i]的关键码小于其前驱，需要将arr[i]插入有序表
            arr[0] = arr[i];//复制为哨兵，arr[0]不存放元素
            for(int j = i-1; arr[0].key < arr[j].key; --j){//从后往前查找待插入位置
                arr[j+1] = arr[j];//向后挪位
            }
            arr[j+1] = arr[0];//复制到插入位置
        }
    }
}

1.1.1.3 性能分析

稳定性： 稳定

适用性： 顺序存储和链式存储的线性表

时间复杂度：平均时间复杂度 O( $n^{2}$ ) 最好情况 O(n) 最坏情况 O( $n^{2}$ )

空间复杂度：O(1)

关键字比较次数 KCN = (n+2)(n-1)/2 ≈ $a^{2}$

记录移动次数RMN = (n+4)(n-1)/2 ≈ $\frac{n^{2}}{2}$

1.1.2折半插入排序

1.1.2.1 算法思想

基本的排序思想与直接插入排序的思想相同。不同点在于：在查找插入位置的时候，并非遍历数组，而是采用二分查找的思想查找到应插入的位置，再统一向后移动数组，插入元素。

1.1.2.2 算法实现

//顺序表实现
void InsertSort(int a[], int n){
    int i, j, l, r, mid;
    for(int i = 2; i <= n; i++){//将a[2]~a[n]插入前面的已排序序列
        a[0] = a[i];//将a[i]暂存到a[0]
        l = 1; r = i-1;//设置折半查找的范围
        while(l <= r){//折半查找（默认递增有序）
            mid = (l + r) / 2;//取中间点
            if(a[mid].key > a[0].key)//查找左子表
                h = mid - 1;
            else l = mid + 1;//查找右子表
        }
        for(j = i - 1; j >= h + 1; --j)
            a[j+1] = a[j];//统一后移元素，空出插入位置
        a[r+1] = a[0];//插入操作
    }
}

1.1.1.3 性能分析

稳定性： 稳定

适用性： 顺序存储

时间复杂度：O(