本文深入解析逻辑推理中的充分条件、必要条件及其应用，通过实例讲解如何区分和使用这些概念，帮助读者掌握公务员考试中逻辑题的解题技巧。
当的时候 c属于A 为前面的充分条件
仅当的时候 c属于A为前面的必要条件
充分条件：
如果条件A是结论B的充分条件：A与其他条件是并连关系，即A、C、D….中任意一个存在都可以使得B成立（就像是个人英雄主义），如下图：
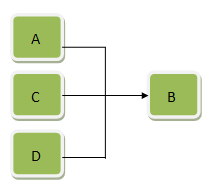
用法：
1．如果条件A存在，B肯定成立，即A→B（箭头表示能够推导出）
2．如果B不成立，则说明所有可能的条件都不存在，因此A肯定也不存在，即非B→非A
3．如果条件A不存在，而条件C、D可能存在，也可以使得B成立，即不能导出非A→非B
必要条件：
条件A是结论B的必要条件：A与其他条件是串联关系，即条件A必须存在，且条件C、D….也全部存在才可能导致B结论。（团结的力量）如下图：
用法：
我简单表示为A+…→B(中间的点表示还有其他条件)
1．如果B成立了，说明所有条件都存在，肯定存在条件A。即B→A。
2．如果条件A不存在，串联少了一个条件，B也肯定不能成立，即 非A→非B。
3．如果B不成立，可能是C，D不存在但A存在，只是C、D掉链子了，即不能导出 非B→非A。
试题中的用法：
先判断出各个关键词之间是充分还是必要关系，然后用关键词和箭头画出之间的关系，例如：A是B的充分条件，A’是B的必要条件，则画出来A→B←.....+A’，然后根据必要条件A’+…→B能推导成B→A’的特点转化为A→B→A’
然后根据四个正确推论：A→B ，非B→非A，B→A’，非A’→非B和
两个错误推论：非A→非B ，非B→非A’即可进行判断。
对于公务员考试中此类题的简单解题方法，我在专栏里做了详细介绍，需要的话请移步专栏：充分必要条件 - 简单解题方法，如果完全理解消化了的话，应该就能很顺利地解决这类题目了。
下面先举一个例子简单说明试题中的做法：
例题：只有住在广江市的人才能够不理睬通货膨胀的影响;如果住在广江市，就得要付税;每一个付税的人都要发牢骚。
根据上述判断，可以推出以下哪项一定是真的?
(1)每一个不理睬通货膨胀影响的人都要付税。
(2)不发牢骚的人中没有一个能够不理睬通货膨胀的影响。
(3)每一个发牢骚的人都能够不理睬通货膨胀的影响
分析：先一句句分析：
只有住在广江市的人才能够不理睬通货膨胀的影响
“只有。。。才。。。”在这里表示必要条件，“住在广江市”是“不理睬通货膨胀”的必要条件，但是不充分（因为有可能不光“住在九江”，还得“有九江户口”等条件才能“不理睬通货膨胀”），标记为：住在广江市+...→不理睬通货膨胀，根据必要条件A+…→B的正确推论B→A的特点，转化为：不理睬通货膨胀→住在广江市。
（注：“只有。。。才。。。”也可能表示充分必要条件，区别是这个条件是不是导致结论的唯一条件。比如“只有触犯了刑法才按照刑法进行处罚”，“触犯了刑法”是“按照刑法进行处罚”的唯一条件，因此是充分必要条件。而本题中，仅仅“住在广江市”，如果没有收入等，那也不能够“不理睬通货膨胀”，因此需要其他条件进行串联才能够导致“不理睬通货膨胀”，因此在此题中是仅仅是必要条件而不是充分必要条件。）
如果住在广江市，就得要付税
“如果。。。就。。。”表示充分条件，住在广江市是付税的充分条件，标记为：住在广江市→付税。
每一个付税的人都要发牢骚
“。。。都要。。。”也表示充分条件，付税是发牢骚的充分条件，标记为：付税→发牢骚。
然后连起来就是：不理睬通货膨胀→住在广江市→付税→发牢骚。
对于（1），根据上面画出来的推导链条，充分条件能连续推导，很明显是对的。
对于（2），根据充分条件推理的非B→非A的特点，以不发牢骚为起点反推，不发牢骚→不付税，不付税→不住在广江市，不住在广江市→理睬通货膨胀，也就是说没有人能够不理睬（双重否定即肯定），因此（2）也正确。
对于（3），由于充分条件推理只能非B→非A，不能够B→A，因此推导不回去。
注：判断是“充分条件”还是“必要条件”还是“充分必要条件”，最好不记关键词而是应该理解判断表达的意思，因为很多句子没有“只有”、“才”、“就”等关键词。
如果条件能够导致后面的结论，那就是充分条件，比如“住在九江要付税”，可以理解出“住在九江”已经能够导致“付税”成立，那么“住在九江”就是“付税”的充分条件；
如果结论想要成立必须需要前面的条件，就是必要条件，如“付税需要住在九江”，可以理解出“住在九江”是“付税的一个条件，但可能需要其他条件，比如“月薪需要超过3500”，因此“住在九江”就是“付税”的必要条件，表示很必要，但是还不够充分导致结论；
如果前面的条件是后面结论成立的唯一条件，那么就相互是充分必要条件。这个比较容易判断。
，对于你提的问题，我试着推导解释了一下，请批判式阅读。
1、如果p是q的充分条件，那么q一定是p的必要条件。
解释：“p是q的充分条件”，根据充分条件图：
如果q（B）不成立，则说明所有可能的条件都不存在，因此p（A）肯定也不存在，也就是说q的存在对于p的存在是必要的。因此q一定是p的必要条件。
2、如果p是q的必要条件，q一定是p的充分条件。
解释：“p是q的必要条件”，根据必要条件图：
如果q（B）成立，则说明包括p（A）在内所有可能的条件肯定都存在，因此p（A）肯定也存在，也就是说q的存在对于p的存在已经很充分，不需要别的其他条件。因此q一定是p的充分条件。
3、p对于q是不充分的，q对于p一定不必要。
分两种情况：
1）p对于q是必要不充分的，那么q对于p一定是充分不必要条件。
解释：“p对于q是必要不充分的”，根据必要条件图：
如果q（B）成立，则说明包括p（A）在内所有可能的条件肯定都存在，因此p（A）肯定也存在，也就是说q的存在对于p的存在已经很充分，不需要别的其他条件。因此q一定是p的充分条件。
“p对于q不充分”是说除了p必须还有其他条件共同存在才能导致q存在。只能推断出p和q不是充分必要条件。这句话不能得出其他推论。
在“q是p的充分条件”的基础上，假如q也是p的必要条件，那么q就是p的充分必要条件，那么p也是q的充分必要条件，与1）“p对于q是必要不充分的”相矛盾，且与“p和q不是充分必要条件”相矛盾，因此q不是p的必要条件。
因此，q对于p一定是充分不必要条件。
2）p对于q是不必要不充分的，那么q对于p不充分也不必要。
解释：“p对于q是不必要不充分的”，则p和q没有任何关系，因此q对于p不充分也不必要。
综合1）和2），q对于p一定不必要。
4、如果p对于q不必要，q对于p一定不充分。
分两种情况：
1）p对于q充分不必要，那么q对于p一定必要不充分。
解释：“p对于q是充分不必要的”，根据充分条件图：
“p对于q是充分的”，就是说如果q（B）不成立，则说明所有可能的条件都不存在，因此p（A）肯定也不存在，也就是说q的存在对于p的存在是很必要的。因此q一定是p的必要条件。
“p对于q是不必要的”，说明不一定需要p存在，而是存在其他条件也能够导致q存在，因此q存在不一定是因为p存在，还有可能是其他条件存在，因此q的存在不能推导出p存在，因此q是p的不充分条件。
因此，q对于p一定是必要不充分条件。
2）p对于q不充分不必要，那么q对于p一定不必要也不充分。
解释：“p对于q是不充分不必要”，则p和q没有任何关系，因此q对于p不必要也不充分。
综合1）和2），q对于p一定不充分。
扫一扫
1095
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
