454.四数相加II 383. 赎金信 15. 三数之和 18. 四数之和

454.四数相加II

1.自己思路

没有比较好的解题思路 感觉重点在于利用题目给的数组长度相等

数据结构选用map 因为需要记录下标和下标对应的数值

2.题解思路

四个数组两两分组 计算值 复杂度n的平方

map key存放前两个数组的相加值 value计算次数（因为返回次数 而不是下标）

编写一次通过（注意auto的使用与访问first 与 second）

383. 赎金信

1.自己思路：

一个map key 为26字母对应的int value为次数 先遍历A 存入map 然后遍历B 存入map 次数--

最后遍历整个map 若是出现value>0则false 复杂度 n 通过

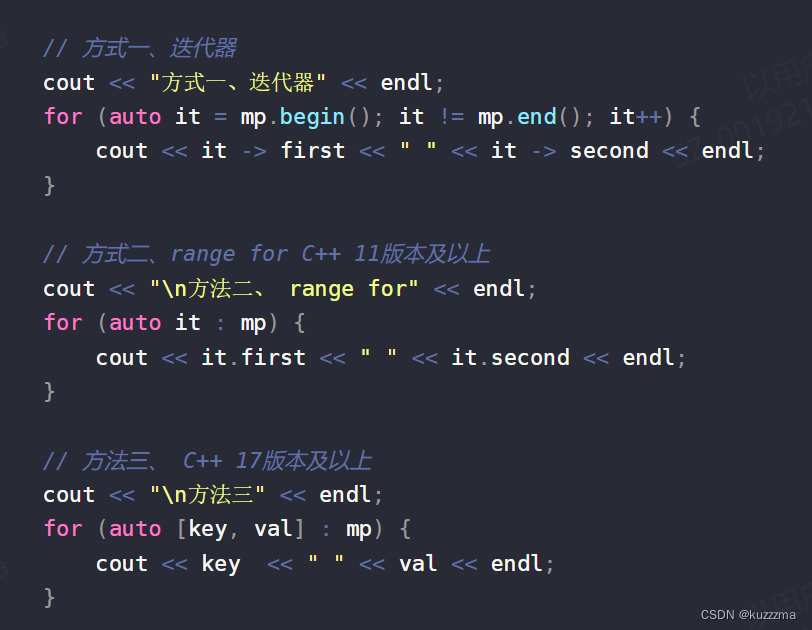
2.题解思路：

可以使用数组来存结果 下标为字母 下标对应数组为次数

15. 三数之和

1.自己思路

暴力解法 但是没办法去重

2.题解思路

双指针吧  一共三层遍历 i left right  left为i的下一个 right为最后一个 注意！！！前提是已经排序好（包含重复元素）i left right 相加大于0 right需要-- 小于0 left++

关键点在于去重！！！i需要与左比较而不是和右比较 因为和右相同可能和为0（此时i已经去重 对于left right 来说 i 不会再变化）

循环找left right终止条件 right>left（可以自己举例子判断边缘条件）

left right的双去重分别与下一个元素比较 然后对应操作

最后找到答案时 left与right收缩

完成

18. 四数之和

1.自己思路

延续三数之和 多一层for循环 但是判断条件不准确 通过率0

2.题解思路

负数相加 和更小 所以判断条件变化 k>0 target>0 才可以进行k>target的剪枝操作

去重操作 k去重 i= k+1 i去重有变化 同三数之和的Left

第一次写少了i的剪枝操作

第二次出错在于去重是用if continue的因为外面已经有循环（对于非left与right的去重）！！！